ÁREAS LIMITADAS DOS FUNCIONES
ÁREAS LIMITADAS POR DOS FUNCIONES. APLICACIONES DE LA INTEGRAL DEFINIDA:
PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- APLICACIONES DE LA INTEGRAL DEFINIDA PARA EL CÁLCULO DE ÁREAS:
-
- CÁLCULO DE INTEGRALES PARA MATEMÁTICAS DE BACHILLERATO
- INTEGRALES ARCOSENO Y ARCOTANGENTE, EJERCICIOS RESUELTOS
- MÉTODO DE INTEGRACIÓN POR SUSTITUCIÓN O CAMBIO DE VARIABLE. EJEMPLOS RESUELTOS
- EJERCICIOS RESUELTOS DE INTEGRALES POR SUSTITUCIÓN O CAMBIO DE VARIABLE PARA MATEMÁTICAS DE 2º DE BACHILLERATO
- MÉTODO DE INTEGRACIÓN POR PARTES DE RESOLUCIÓN DE INTEGRALES PARA BACHILLERATO
- INTEGRACIÓN DE FUNCIONES RACIONALES
SIGUE EL PROCESO DETERMINADO POR:
ÁREA DEL RECINTO DONDE INTERVIENEN DOS FUNCIONES:
En General el área encerrada por dos funciones f(x) y g(x):
![]()
Es decir «la integral definida entre los puntos de corte entre las dos funciones, de la resta de las dos funciones que generan el recinto».
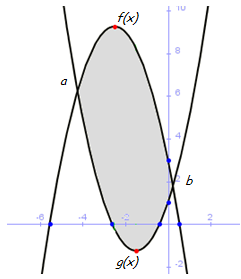
En este ejemplo que se muestra, la función f(x), parábola abierta hacia abajo (la función que está por encima) corresponde a: f(x) = – x2 – 5x + 3
Y la función que se encuentra por debajo, g(x), parábola abierta hacia arriba corresponde a: f(x) = x2 + 3x + 1
Si la primera de las funciones de la integral (la que equivale al minuendo de la resta) es la que está por encima, el resultado de la integral es positivo, correspondiendo al valor del área.
Si por el contrario lo hacemos al revés, el resultado de la integral es negativa. El área entonces corresponde al resultado de la integral cambiado de signo.
Por ello debemos tener en cuenta:
- a y b son los puntos de corte de las dos funciones, que se pueden calcular resolviendo el sistema formado por las dos funciones, normalmente por igualación de ellas.
- Si el resultado da negativo es porque la función f(x) no es la que está por encima de g(x).
Si las funciones se cortan en varios puntos, no se puede hacer la integral en un solo golpe, sino a trozos, definidos por los sucesivos cortes de las funciones entre sí, para que resultados de áreas positivas no compensen a las negativas.
El siguiente ejemplo corresponde concretamente a estas dos funciones:
f(x) = 3x3 + 2x2 – 3x + 1
g(x) = 2x3 – 2x2 + 5x + 1
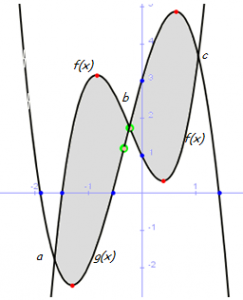
En este caso, debemos tener en cuenta que la función que inicialmente está por encima, en el siguiente recinto se encuentra por debajo, con lo cual lo mejor es recurrir a los valores absolutos, de las integrales subdivididas con los puntos de corte ordenados. Por ello:
![]()
o con los valores absolutos y despreocupándonos de qué función se encuentra por encima en cada tramo:
![]()
CONTINUAR CON:


