EXAMEN ECUACIONES SISTEMAS BACHILLERATO
EXAMEN DE ECUACIONES Y SISTEMAS RESUELTO PARA MATEMÁTICAS I DE 1º BACHILLERATO. PRUEBA 1 DEL SEGUNDO TRIMESTRE. CURSO 2025-26, REALIZADO EN «EL PILAR» :
PRUEBA EVALUADORA QUE INCLUYE SABERES BÁSICOS DE MATEMÁTICAS DE 1º DE BACHILLERATO CIENCIAS RELATIVOS A:
-
- TRIGONOMETRÍA: ECUACIONES TRIGONOMÉTRICAS
- MATERIALES DE ÁLGEBRA PARA 1º DE BACHILLERATO. ECUACIONES
- REGLA DE CRAMER. SISTEMAS DE ECUACIONES PARA BACHILLERATO
- SISTEMAS DE ECUACIONES LOGARÍTMICOS Y EXPONENCIALES RESUELTOS. MATEMÁTICAS BACHILLERATO
- ECUACIONES EXPONENCIALES PARA MATEMÁTICAS DE SECUNDARIA Y BACHILLERATO
- BASADO EN EL SIMULACRO PROPUESTO PREVIAMENTE: SIMULACRO DE EXAMEN PARA MATEMÁTICAS I DE 1º DE BACHILLERATO. ECUACIONES Y SISTEMAS. SEGUNDO TRIMESTRE 2025-26
MÁS RECURSOS DISPONIBLES PARA MATEMÁTICAS DE 1º DE BACHILLERATO: MATEMÁTICAS 1º DE BACHILLERATO
SIGUE EL PROCESO DETERMINADO SEGÚN: MATEMÁTICAS I DE 1º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
EL ENUNCIADO DE LA PRUEBA DE EXAMEN (X1093):
X1093 MAT I 1º BAC 2TRIM PRUEBA1 2526LOS EJERCICIOS DE LA PRUEBA Y SU RESOLUCIÓN PASO A PASO:
EJERCICIO M1BE3419:
Resolver la siguiente ecuación trigonométrica:
2 sen2 x = 1 + cos x
RESOLUCIÓN PASO A PASO DEL EJERCICIO:
EJERCICIO M1BE3419 ECUACIÓN TRIGONOMÉTRICA_V1
EJERCICIO M1BE2119:
Resolver la siguiente ecuación trigonométrica:
cos 2x – 3 cos x + 2 = 0
RESOLUCIÓN PASO A PASO DEL EJERCICIO:
EJERCICIO M1BE2119 ECUACIÓN TRIGONOMÉTRICA_V1
EJERCICIO M1BE3423:
Resolver la siguiente ecuación exponencial:
22x-1 – 5·2x-1 + 2 = 0
RESOLUCIÓN PASO A PASO DEL EJERCICIO:
EJERCICIO M1BE3423 ECUACIÓN EXPONENCIAL_V1
EJERCICIO M1BE3444:
Resolver el siguiente sistema de ecuaciones logarítmicas, comprobando las soluciones:
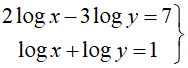
RESOLUCIÓN PASO A PASO DEL EJERCICIO:
EJERCICIO M1BE3444 SISTEMA ECUACIONES LOGARÍTMICAS__V1
EJERCICIO M1BE3422:
Un proveedor de plataneras en Canarias para su cultivo tiene tres tipos de variedades de uso frecuente para plantar: Cavendish, Gros-Michel y Gran Enana. El precio medio de los tres tipos de plataneras es de 2 €. Un modesto agricultor compra para su finca 3 plantas Cavendish y 2 de las Gran Enana, pagando 12 €. Otro compra 4 plantas Gros-Michel y 1 de las Gran Enana para probar, pagando 7 €. Planteando el sistema de ecuaciones correspondiente, responder a las siguientes cuestiones:
a.- Utilizando el Método de Cramer, hallar el precio de las plataneras para plantar del tipo Cavendish.
b.- Hallar el precio de las otras dos variedades de plataneras, como se desee.
RESOLUCIÓN PASO A PASO DEL EJERCICIO:
EJERCICIO M1BE3422 SISTEMA ECUACIONES MÉTODO CRAMER PLATANERAS__V1