INTEGRAL DEFINIDA REGLA BARROW
INTEGRAL DEFINIDA. REGLA DE BARROW. APLICACIONES: CÁLCULO DE ÁREAS:
PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- APLICACIONES DE LA INTEGRAL DEFINIDA PARA EL CÁLCULO DE ÁREAS:
- CÁLCULO DE INTEGRALES PARA MATEMÁTICAS DE BACHILLERATO
- INTEGRALES ARCOSENO Y ARCOTANGENTE, EJERCICIOS RESUELTOS
- MÉTODO DE INTEGRACIÓN POR SUSTITUCIÓN O CAMBIO DE VARIABLE. EJEMPLOS RESUELTOS
- EJERCICIOS RESUELTOS DE INTEGRALES POR SUSTITUCIÓN O CAMBIO DE VARIABLE PARA MATEMÁTICAS DE 2º DE BACHILLERATO
- MÉTODO DE INTEGRACIÓN POR PARTES DE RESOLUCIÓN DE INTEGRALES PARA BACHILLERATO
- INTEGRACIÓN DE FUNCIONES RACIONALES
SIGUE EL PROCESO DETERMINADO POR:
INTEGRAL DEFINIDA:
Se dice integral definida, ya que se calcula entre dos límites de integración (superior e inferior) que se indican por encima y debajo del símbolo de integral:
![]()
OBTENCIÓN DEL VALOR DE LA INTEGRAL DEFINIDA SEGÚN LA REGLA DE BARROW. UTILIZACIÓN PARA EL CÁLCULO DE ÁREAS:
![]()
Siendo F(x) una primitiva de f(x), esto es: F(x) es el resultado de la integral indefinida de f(x)
La forma de trabajar habitual es la siguiente:
Se resuelve la integral como si fuera indefinida (se obtiene la primitiva F(x)) y se introduce entre corchetes, indicando los límites de integración superior e inferior; en el siguiente paso se sustituye la x de la expresión de la integral resuelta (primitiva) primero por el límite superior F(b) y se le resta la expresión sustituida la x por el límite inferior F(a), tal como indica la regla de Barrow. Hay que tener cuidado con los signos, ya que se producen muchos errores.
EJERCICIO DE EJEMPLO M2BE3460:
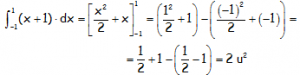
Hemos puesto u2 (unidades cuadradas) ya que:
«La integral definida equivale al área encerrada entre f(x) y el eje de las x, entre los puntos de abscisas x=a y x=b»
Esto se puede comprobar fácilmente en el ejemplo siguiente, donde tenemos representada la recta y=x+1, que es la función que hemos integrado entre los límites de integración x=-1 y x=1.
Hemos sombreado el área del recinto que queda entre la función, el eje OX en la zona comprendida entre x=-1 y x=1.
Observar que el área encerrada por la función y el eje de las x, corresponde a dos unidades cuadradas, 1 entera y dos mitades, esto es 2 unidades cuadradas de área.