EJERCICIO RESUELTO INTEGRAL IRRACIONAL
EJERCICIO RESUELTO M2BE1894 DE INTEGRALES IRRACIONALES:
PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- MÉTODO DE INTEGRACIÓN PARA INTEGRALES IRRACIONALES. CÁLCULO INTEGRAL
- MÉTODOS DE INTEGRACIÓN PARA INTEGRALES TRIGONOMÉTRICAS
- MÉTODO DE INTEGRACIÓN POR SUSTITUCIÓN O CAMBIO DE VARIABLE. EJEMPLOS RESUELTOS
- MÉTODO DE INTEGRACIÓN POR PARTES DE RESOLUCIÓN DE INTEGRALES PARA BACHILLERATO
- INTEGRACIÓN DE FUNCIONES RACIONALES
SIGUE EL PROCESO DETERMINADO POR:
- MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
- Y PUEDE TENER UTILIDAD EN: AYUDANDO A NUESTROS ALUMNOS QUE ESTÁN EN LA UNIVERSIDAD
INTEGRALES IRRACIONALES:
Son aquellas en las que la variable se encuentra sometida a una raiz.
La mayoría de las que nos solemos encontrar se encuentran en alguno de los siguientes tipos, que se transforman en INTEGRALES RACIONALES, haciendo utilizando las SUSTITUCIONES que se proponen:
Los tipos de integrales que vamos a tratar, los agrupamos en cuatro bloques, indicando la estrategia apropiada:
![]()
![]()
![]()
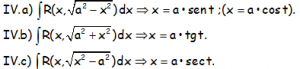
INTEGRAL DEL TIPO III:
![]()
EJERCICIO M2BE1894:
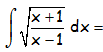
RESOLUCIÓN DE LA INTEGRAL IRRACIONAL:
La sustitución que propone el MÉTODO DE INTEGRALES IRRACIONALES PARA ESTE TIPO, y sus implicaciones en diferenciales:
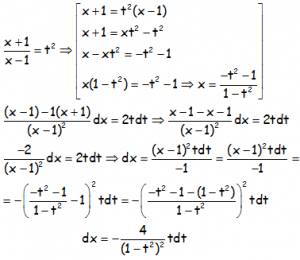
Con lo que la integral se transforma en:
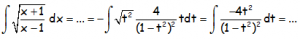
Que es una integral racional con raíces reales múltiples, en la que hay que utilizar el Método de los Coeficientes indeterminados, para INTEGRALES RACIONALES:
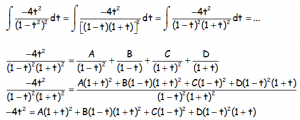
Dando a t valores convenientes para obtener A, B, C y D:
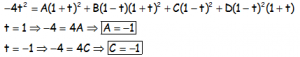
Como con todas las múltiples, nos toca dar otros valores cualquiera, teniendo en cuenta los valores de A y C calculados y resolver el sistema:
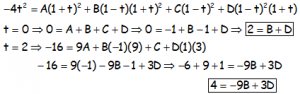
Resolviendo el sistema:
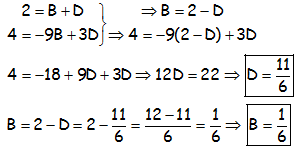
Con lo que la integral pedida:
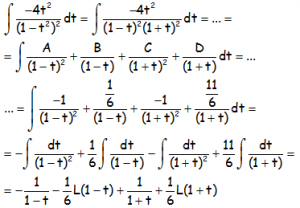
Que recuperando la variable original, cambiando la t por la x:
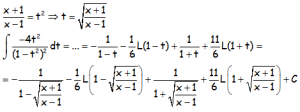
Que como se puede ver es una BARBARIDAD DE EJERCICIO !!


