FUNCIONES RECTAS CARACTERÍSTICAS REPRESENTACIÓN
FUNCIONES POLINÓMICAS DE PRIMER GRADO. RECTAS. CARACTERÍSTICAS Y REPRESENTACIÓN:

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
FORMA PARTE DE LOS MATERIALES DE LAS PROGRAMACIONES DIDÁCTICAS:
RECTAS: PENDIENTE Y ORDENADA EN EL ORIGEN.
Las funciones polinómicas de primer grado del tipo: f(x) = m·x + n; a la hora de representarlas nos dan rectas.
El valor de m es la pendiente de la recta
n es la ordenada en el origen.
La PENDIENTE nos da idea de la inclinación de la recta. Matemáticamente es la tangente del ángulo que forma la recta con la horizontal.
En cualquier caso lo que nos interesa es qué significa esto de la pendiente (m) y la ordenada en el origen (n) desde un punto de vista gráfico, para la recta y = mx + n:
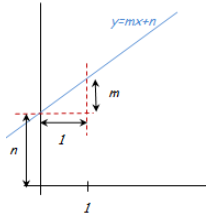
Lo que indica la ORDENADA EN EL ORIGEN n está muy claro, representa el punto de corte con el eje de las Y (con el eje de ordenadas), de ahí lo de “ordenada en el origen”.
RESPECTO A LA PENDIENTE:
-
- La pendiente es mayor cuanto más inclinada esté la recta:
- Una recta horizontal no tiene pendiente, no tiene inclinación, su pendiente es cero.
- Si está inclinada hacia arriba como en el ejemplo la pendiente es positiva
- Si está inclinada hacia abajo la pendiente es negativa.
Para interpretar la pendiente en el dibujo de una recta, o para dibujar una recta de la que nos dan los datos: pendiente y ordenada en el origen, lo mejor es:
Partiendo del punto de corte con el eje de las y, caminar una unidad en la horizontal y después subir tantas unidades como nos indique la pendiente (si es positiva) o bajar esas unidades si es negativa. Al unir el punto de corte con el eje de las Y, con el punto final de “avanzar una unidad en la horizontal y subir (o bajar) tantas como nos indique m” se obtiene la recta.
EJEMPLO DE RECTA CON PENDIENTE POSITIVA:
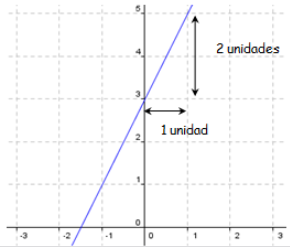
Hemos representado a continuación en azul, la recta: y=2x+3 [pendiente=2, ordenada en el origen=3]; notar como el punto de “choque”, de corte con el eje vertical, de la Y es 3 (ordenada en el origen) y la pendiente es tal que por cada unidad que “patea” en la horizontal sube dos unidades en la vertical:
EJEMPLO DE RECTA CON PENDIENTE NEGATIVA:
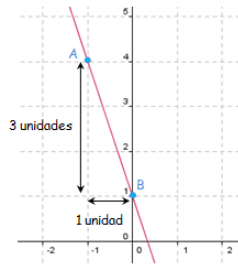
Hemos representado a continuación en rojo, la recta y=-3x+1 [pendiente=-3, ordenada en el origen=1]; notar como el punto de “choque” de corte con el eje vertical, de la Y es 1 (ordenada en el origen) y la pendiente es tal que por cada unidad que “patea” en la horizontal baja dos unidades en la vertical (ya que la pendiente es negativa):
También podemos siempre representar la recta dando valores a las x y obteniendo la componente y que le corresponde, al menos para dos puntos. La representación de esos dos puntos y su unión mediante una línea recta nos representa la función lineal.
ECUACIÓN DE UNA RECTA CONOCIDOS DOS PUNTOS DE LA MISMA:
PARA OBTENER LA ECUACIÓN DE UNA RECTA CONOCIDOS DOS PUNTOS, que nos aportan como dato o que sacamos nosotros de la gráfica, podemos utilizar la ECUACIÓN DE LA RECTA QUE PASA POR DOS PUNTOS, A(x1,y1) y B(x2,y2):
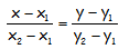
EJEMPLO DE OBTENCIÓN DE LA ECUACIÓN DE UNA RECTA CONOCIDOS DOS PUNTOS:
Vamos a obtener la recta roja, del dibujo anterior, utilizando dos de los puntos que cogemos de la gráfica. Utilizaremos los marcados en azul que son el A(-1,4) y B(0,1)
Utilizando la Fórmula de ECUACIÓN DE LA RECTA QUE PASA POR DOS PUNTOS:
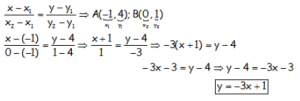
Que es lo que nos tenía que dar, efectivamente la ecuación de la recta roja.
OBTENCIÓN DE LA PENDIENTE DE UNA RECTA, CONOCIDOS DOS PUNTOS A(x1,y1) y B(x2,y2):
Teniendo en cuenta que la pendiente es la tangente del ángulo que forma la recta con la horizontal (esto es: cateto opuesto/cateto contiguo), podemos elegir un triángulo cualquiera en la recta y obtener la pendiente haciendo:

Que en el mismo EJEMPLO de la recta roja (y=-3x+1) con los puntos A(-1,4) y B(0,1), extraídos de la representación:
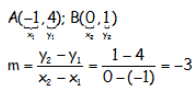
Que es lo que tenía que darnos.
EJERCICIOS RESUELTOS DE RECTAS, DE FUNCIONES LINEALES POLINÓMICAS DE PRIMER GRADO:
EJERCICIO M4EP310:
Calcular las ecuaciones de las rectas siguientes, sabiendo que:
a) Esta es su representación gráfica:
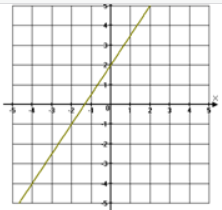
b) Tiene una ordenada en el origen -2 y pendiente 1.
c) m= -1 y n= 3
d) La pendiente es 3 y pasa por el punto A(-2,0).
e) La ordenada en el origen es 1 y pasa por el punto A(-2,2)
f) Pasa por los puntos: A(1,2) y B(-1,3)
g) Esta es su gráfica:
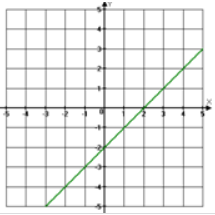
h) Ordenada en el origen 1 y pendiente 3.
i) m= 1/2 y n= -4
j) La pendiente es 1 y pasa por el punto A(2,3)
k) La ordenada en el origen es 2 y pasa por el punto A(-1,2)
l) Pasa por los puntos: A(-1,-2) y B(-2,3):
IR AL ARTÍCULO CON LA RESOLUCIÓN DETALLADA DE ESTE EJERCICIO Y SUS APARTADOS: EJERCICIO RESUELTO DE FUNCIONES LINEALES. RECTAS: CARACTERÍSTICAS Y REPRESENTACIÓN
