EJERCICIOS RESUELTOS PROPIEDADES LOGARITMOS
EJERCICIOS RESUELTOS DE APLICACIÓN DE LAS PROPIEDADES DE LOS LOGARITMOS. ARITMÉTICA PARA BACHILLERATO:

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- ARITMÉTICA PARA SECUNDARIA Y 1º DE BACHILLERATO
- UTILIDAD DE LOS LOGARITMOS. LEYES DE KEPLER
- ECUACIONES LOGARÍTMICAS PARA MATEMÁTICAS DE SECUNDARIA Y BACHILLERATO
- SISTEMAS DE ECUACIONES LOGARÍTMICAS
ESTE MATERIAL SIGUE EL PROCESO DETERMINADO POR:
- MATEMÁTICAS I DE 1º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
- MATEMÁTICAS DE 4º DE LA E.S.O.. DESARROLLO DE LA ASIGNATURA
DEFINICIÓN DE LA OPERACIÓN LOGARITMO:
![]()
CONSECUENCIAS DE LA DEFINICIÓN DE LOGARITMO:
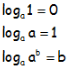
PROPIEDADES DE LOS LOGARITMOS:
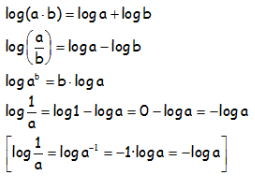
EJERCICIO M1BE3291:
Calcular utilizando la definición de logaritmo el valor de la siguiente expresión:
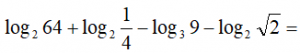
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M1BE3291 DE APLICACIÓN DE LAS PROPIEDADES DE LOS LOGARITMOS. ARITMÉTICA PARA BACHILLERATO
EJERCICIO M1BE3228:
Obtener el valor de esta expresión con logaritmos de base 2, sin calculadora, utilizando exclusivamente las propiedades de los logaritmos:
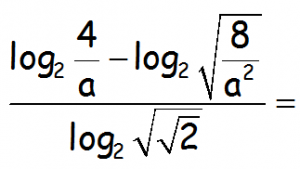
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/jjUA7EcbZ7M
EJERCICIO M1BE3307:
Sabiendo que log 2 = 0,3010 y log 7 = 0,8451, sin calculadora y exclusivamente utilizando las propiedades de los logaritmos, obtener el valor de los siguientes logaritmos:
a.- log 56 =
b.- log g = log 9,8 =
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN RESUELTO DE ARITMÉTICA MATEMÁTICAS I 1º DE BACHILLERATO, PRIMER TRIMESTRE DEL CURSO 2025-26.
EJERCICIO M1BE2308:
Si log 3 = 0,4771 y log 5 = 0,6990
Calcular: a) log 50 b) log 81 c) log 125 d) log 9/25
IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE OPERACIONES CON LOGARITMOS
EJERCICIO M1BE2597:
Sabiendo que log 2 = 0,3010 y log 7 = 0,8451, calcular:
a.- log 0,875 =
b.- log 28 =
IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: EXAMEN INICIAL RESUELTO DE ARITMÉTICA Y ÁLGEBRA PARA MATEMÁTICAS I, DE 1º DE BACHILLERATO. CURSO 2024-25
EJERCICIO M1BP0339:
Sabiendo que log 2 = 0,3010 y log 3 = 0,4771, calcular con una calculadora de parvulitos (sin tecla log):
a.- log 14,4 =
b.- log (1,6 · 0,32) =
c.- log 5,12 =
d.- log 16,2 =
e.- log 0,3 =
f.- log 0,02 =
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M1BE0339 DE APLICACIÓN DE LAS PROPIEDADES DE LOS LOGARITMOS. ARITMÉTICA PARA BACHILLERATO
EJERCICIO M1BE3292:
Calcula el valor de los siguientes logaritmos, sin calculadora:
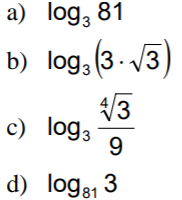
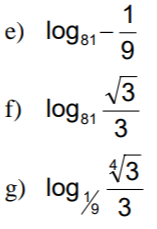
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M1BE3292 DE APLICACIÓN DE LAS PROPIEDADES DE LOS LOGARITMOS. ARITMÉTICA PARA BACHILLERATO
EJERCICIO M1BE3293:
Sabiendo que log 2 = 0,3010 y log 3 = 0,4771, calcular:
a.- log 0,00000002
b.- log 0,125
c.- log 5
d.- log 72
e.- log 60
f.- log 18
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M1BE3293 DE APLICACIÓN DE LAS PROPIEDADES DE LOS LOGARITMOS. ARITMÉTICA PARA BACHILLERATO
EJERCICIO M4EE3481:
Si el log 3 = 0,5 y el log 7 = 0,8, calcular sin utilizar la calculadora:
a.- log 21 =
b.- log (9/7) =
c.- log 49 =
d.- log 0,3 =
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO FQ1BE3481 DE TRABAJO Y ENERGÍA VS DINÁMICA PARA FÍSICA DE BACHILLERATO
EJERCICIO M1BE1924:
Hallar sin calculadora el valor numérico de la siguiente expresión con logaritmos neperianos (logaritmos en base e).
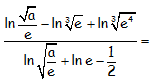
SOLUCIÓN: 1
IR AL ARTÍCULO CON LA RESOLUCIÓN DETALLADA DEL EJERCICIO: EJERCICIOS CON SOLUCIÓN DE UTILIZACIÓN DE LAS PROPIEDADES DE LOS LOGARITMOS
EJERCICIO M1BE1925:
Hallar sin calculadora, utilizando las propiedades de los logaritmos, el valor numérico de las siguientes expresiones con logaritmos en base dos:
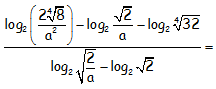
SOLUCIÓN: 2
IR AL ARTÍCULO CON LA RESOLUCIÓN DETALLADA DEL EJERCICIO: EJERCICIOS CON SOLUCIÓN DE UTILIZACIÓN DE LAS PROPIEDADES DE LOS LOGARITMOS
EJERCICIO M1BE1926:
Demostrar, desarrollando y utilizando las propiedades de los logaritmos, que la siguiente expresión con logaritmos decimales (en base 10), es equivalente a la mitad del logaritmo decimal de b.
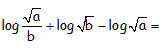
IR AL ARTÍCULO CON LA RESOLUCIÓN DETALLADA DEL EJERCICIO: EJERCICIOS CON SOLUCIÓN DE UTILIZACIÓN DE LAS PROPIEDADES DE LOS LOGARITMOS
EJERCICIO M1BE1927:
Demostrar con rigor, y basándose en las propiedades de los logaritmos, la veracidad o falsedad de la siguiente igualdad con logaritmos en base 3:
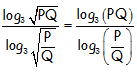
IR AL ARTÍCULO CON LA RESOLUCIÓN DETALLADA DEL EJERCICIO: EJERCICIOS CON SOLUCIÓN DE UTILIZACIÓN DE LAS PROPIEDADES DE LOS LOGARITMOS
EJERCICIO M1BE3461:
Hallar sin calculadora, utilizando las propiedades de los logaritmos, el valor numérico de las siguientes expresiones con logaritmos neperianos (logaritmos en base e):
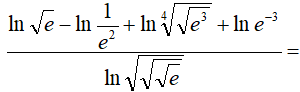
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M1BE3461 DE APLICACIÓN DE LAS PROPIEDADES DE LOS LOGARITMOS. ARITMÉTICA PARA BACHILLERATO
EJERCICIO M1BE3306:
Obtener el valor de la siguiente expresión, exclusivamente utilizando las propiedades de los logaritmos, dejando constancia de los pasos y sin calculadora:
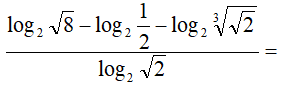
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN RESUELTO DE ARITMÉTICA MATEMÁTICAS I 1º DE BACHILLERATO, PRIMER TRIMESTRE DEL CURSO 2025-26.
