UTILIDAD LOGARITMOS LEYES KEPLER

UTILIDAD DE LOS LOGARITMOS. TERCERA LEY DE KEPLER:

MATEMÁTICAS/FÍSICA Y QUÍMICA 4º E.S.O.

MATEMÁTICAS/FÍSICA Y QUÍMICA 1º BACHILLERATO

FÍSICA 2º BACHILLERATO

ARITMÉTICA, ÁLGEBRA, ANÁLISIS, GRAVITACIÓN

A nadie se le escapa el rechazo que produce en los estudiantes esta operación de los logaritmos. Intentaremos con este artículo/actividad recuperar la simpatía por esta operación, o al menos un enfoque interdepartamental de esta herramienta.

Utilizaremos o pondremos en marcha estrategias relacionadas con:

  • Logaritmos: cálculo y ecuaciones logarítmicas
  • Geometría en dos dimensiones, con la ecuación de la recta que pasa por dos puntos.
  • La función lineal.
  • La Tercera Ley de Kepler.
  • Un poco de historia.
  • El método científico.
  • Y sobre todo, mucha Competencia matemática y en ciencia, tecnología e ingeniería, a través de contenidos de las asignaturas de Matemáticas y Física, para 4º de la E.S.O. y 1º y 2º de Bachillerato.

Este artículo está elaborado para los alumnos, con la intención de ver la utilidad de los logaritmos y motivar el uso de estrategias propias de la investigación en Matemáticas y Física.

RELACIONADO CON LAS ACTIVIDADES DE ESTE PROYECTO:

ASPECTOS FORMALES DE LA ACTIVIDAD:

CON RESPECTO A LOS SABERES BÁSICOS DE FÍSICA Y QUÍMICA DE 1º BACHILLERATO PREDOMINANTES EN LA ACTIVIDAD:

CON RESPECTO A LOS SABERES BÁSICOS DE MATEMÁTICAS DE 1º BACHILLERATO PREDOMINANTES EN LA ACTIVIDAD:

CON RESPECTO A LAS COMPETENCIAS ESPECÍFICAS DE FÍSICA Y QUÍMICA DE 1º DE BACHILLERATO QUE SE CONSIDERAN:

FYQ 1BAC C1 , FYQ 1BAC C2 , FYQ 1BAC C3 , FYQ 1BAC C4 , FYQ 1BAC C5 , FYQ 1BAC C6

CON RESPECTO A LAS COMPETENCIAS ESPECÍFICAS DE MATEMÁTICAS DE 1º DE BACHILLERATO QUE SE CONSIDERAN:

MAT BAC C1 , MAT BAC C2 , MAT BAC C3 , MAT BAC C4 , MAT BAC C5 , MAT BAC C6 , MAT BAC C7 , MAT BAC C8 ,  MAT BAC C9 

SE PRETENDE CON ESTA DINÁMICA EL DESARROLLO DE LAS COMPETENCIAS:

CON RESPECTO A LOS CRITERIOS DE EVALUACIÓN DE MATEMÁTICAS I DE 1º DE BACHILLERATO

MATI1BAC1.1 , MATI1BAC1.2 , MATI1BAC2.1 , MATI1BAC2.2 , MATI1BAC3.1 , MATI1BAC4.1 , MATI1BAC5.1 , MATI1BAC5.2 , MATI1BAC6.1 , MATI1BAC6.2 , MATI1BAC7.1 , MATI1BAC7.2 , MATI1BAC8.1 , MATI1BAC8.2 , MATI1BAC9.1 , MATI1BAC9.2 , MATI1BAC9.3 

ESTE MATERIAL TIENE RELACIÓN CON ASPECTOS DEL PERFIL DE SALIDA DEL ALUMNADO DE LOS INSTITUTOS DIOCESANOS DE CANARIAS

LOS LOGARITMOS:

PODRÍA INTERESAR IR A DEFINICIÓN Y PROPIEDADES DE LOS LOGARITMOS

Son ideales para el tratamiento de comportamientos físico-químicos en los que intervienen números muy grandes (distancias o tiempos astronómicos) o muy pequeños (el pH). Fueron propuestos por primera vez en 1614 por John Napier.

TERCERA LEY DE KEPLER Y UTILIDAD DE LOS LOGARITMOS:

A los que conocemos algo de física siempre nos ha sorprendido que Kepler obtuviera su tercera ley, mirando tablas astronómicas elaboradas por Tycho Brahe (previas a la invención del telescopio por Galileo), antes de que Newton naciera.

Newton con su Segunda Ley, aplicada al movimiento supuesto circular de los planetas alrededor del Sol, y con su Ley de Gravitación Universal confirma la Tercera Ley de Kepler.

Notar que Kepler da por supuesto que los planetas giran alrededor del Sol, lo que Copérnico afirma en su Teoría Heliocéntrica y sorprendentemente mucho antes afirmaba Aristarco de Samos.

Kepler en su tercera Ley, descubre que los radios medios de las órbitas de los planetas del Sistema Solar alrededor del Sol y los periodos (tiempo que cada planeta tarda en dar una vuelta completa) guardan la siguiente relación. Insistimos que lo hizo mirando tablas astronómicas de tiempos y distancias:

Si miramos las tablas de partida, de las distancias (radios medios de las órbitas de cada planeta alrededor del Sol) y de los tiempos que tardan en completar una órbita, observamos que mucho hay que mirar estos números para percatarse de la relación que vió Kepler

Tabla 1:

PLANETA RADIO (m) PERIODO (s)
Mercurio 5,7·1010 7,59·106
Venus 1,08·1011  1,94·107
Tierra  1,5·1011  3,15·107
Marte  2,28·1011  5,92·107
Júpiter  7,8·1011 3,74·108
Saturno  1,43·1012 9,28·108
Urano 2,88·1012 2,65·109
Neptuno 4,51·1012 5,19·109

Si hacemos el logaritmo decimal (logaritmo en base 10) tanto del radio como del periodo y lo incluimos en la tabla:

Tabla 2:

PLANETA RADIO R (m) log10 R PERIODO T (s) log10 T
Mercurio 5,7·1010 10,76 7,59·106 6,88
Venus 1,08·1011 11,03  1,94·107 7,29
Tierra  1,5·1011 11,18  3,15·107 7,50
Marte  2,28·1011 11,36  5,92·107 7,77
Júpiter  7,8·1011 11,89 3,74·108 8,57
Saturno  1,43·1012 12,16 9,28·108 8,97
Urano 2,88·1012 12,46 2,65·109 9,42
Neptuno 4,51·1012 12,65 5,19·109 9,72

Seguramente resulta más fácil, o por lo menos, más fácil de trabajar con ellos.

En cualquier caso, si representamos en un sistema cartesiano, en el eje OX el logaritmo del radio (log R) y en el eje OY el logaritmo del periodo (log T), obtenemos la siguiente gráfica, gráfica 1:

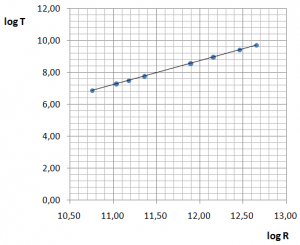
Observamos que las medidas, para cada uno de los planetas, se ajustan casi con total exactitud a una recta, a una función lineal, de la que podemos obtener su ecuación.

ECUACIÓN DE LA RECTA QUE PASA POR DOS PUNTOS A(x0,y0) y B(x1,y1), EN FORMA PUNTO-PENDIENTE; donde m es la pendiente de la recta y (x0,y0) uno de los puntos :

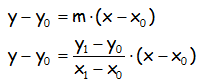
En nuestro caso y considerando los valores de Mercurio (punto A) y Venus (punto B) (subrayados en la tabla 1). Podríamos haber cogido cualquier otro par de puntos:

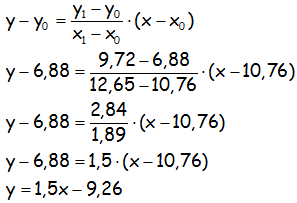
Teniendo en cuenta que 1,5 es claramente 3/2; y teniendo en cuenta que en la gráfica la «y» es el log T y la «x» es el log R, podemos expresar la ecuación de la recta de tendencia, del siguiente modo:

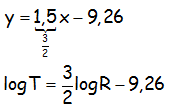
Que jugando con la ecuación logarítmica al objeto de sacar la relación entre el periodo y el radio, para intentar emular a Kepler, nos queda:

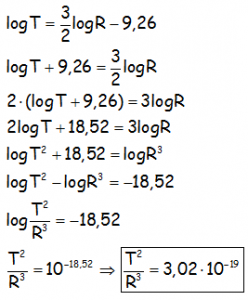
Confirmando lo que obtuvo Kepler en su tercera Ley, que la relación entre el cuadrado del periodo y el cubo de la distancia media al Sol es constante para todos los planetas.

Posteriormente, el valor de la constante se obtiene y coincide con:

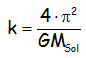
Para todos los planetas que giran en torno al Sol.

La tercera Ley de Kepler también sirve para evaluar el movimiento de la Luna alrededor de la Tierra, o incluso el movimiento de los satélites artificiales en órbita alrededor de la Tierra, teniendo en cuenta que en la constante k hay que poner la masa de la Tierra. Lo mismo para cualquier otro planeta y sus satélites.

Insistimos en que posteriormente a la elaboración de esta Ley por parte de Kepler, Newton la confirma utilizando su Segunda Ley, la Ley de Gravitación Universal y suponiendo el movimiento de los planetas alrededor del Sol como si de un movimiento circular uniforme se tratara. (VER DE CIRCULAR A KEPLER )

POSIBLEMENTE ALGUIEN INTERESADO SE PREGUNTE: ¿Y SI REPRESENTAMOS DIRECTAMENTE EL PERIODO DE LOS PLANETAS FRENTE A SU DISTANCIA AL SOL?, con los datos de la tabla 1, sin los logaritmos.

La gráfica que resulta es la siguiente, gráfica 2:

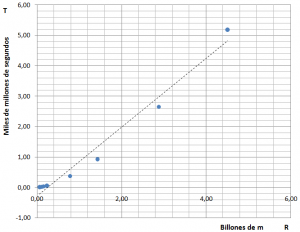
Notar que la línea de tendencia no responde a la realidad, quedando una curva de interpretación más complicada. Fijarse incluso en los 4 primeros planetas en el inicio de la gráfica.

Por lo tanto, se ha puesto de manifiesto la UTILIDAD DE LOS LOGARITMOS, al menos en este caso.

ACTIVIDADES PROPUESTAS:

Con los siguientes datos:

G (Constante de Gravitación Universal) =6,67·10-11 N·m2/kg2.

MSol=1,989·1030 kg.

MTierra=5,972·1024 kg

1.- Confirmar que el valor de la constante de Kepler coincide (o se acerca) al obtenido en el desarrollo expuesto.

2.- Confirmar con la Tierra y los datos de la tabla 1 que se cumple la Tercera Ley de Kepler.

3.- Hallar la distancia entre la Tierra y la Luna.

4.- Realizar una línea de tiempo con todos los científicos y autores mencionados en el artículo.

Post Views: 3.691
On:

Comments are closed, but trackbacks and pingbacks are open.