MOVIMIENTO CIRCULAR KEPLER GRAVITACIÓN

DE MOVIMIENTO CIRCULAR A LAS LEYES DE KEPLER. GRAVITACIÓN EN EL UNIVERSO:MOVIMIENTO CIRCULAR KEPLER GRAVITACIÓNKEPLER GRAVITACIÓN

Se pretende con esta dinámica diseñada inicialmente para Física y Química de 1º de Bachillerato, una vez se ha impartido en Física y Química de 1º de Bachillerato CINEMÁTICA (en lo que respecta a movimientos verticales y parabólicos), DINÁMICA (en lo que respecta al uso de las 3 Leyes de Newton en los ejercicios habituales), integrar el contenido de Cinemática de Movimiento Circular y el contenido de Dinámica de la Ley de Gravitación Universal para llegar hasta la 3ª Ley de Kepler y poder así estudiar el movimiento de Satélites.

INTERESA LA CONSULTA DE:

Supone una vuelta atrás a contenidos impartidos que consolida conocimientos y los aplica al caso que despierta interés en el alumnado del movimiento de satélites.

Como suele ocurrir con esto del Aprendizaje Basado en Proyectos (A.B.P.), en las actividades que se plantean a largo plazo, con posibilidad de incluir nuevas tareas a medida que se imparten, se ha observado el interés de mostrarlas a los alumnos de Física y Química de 4º de la ESO, dentro del apartado de Dinámica de Fuerzas en la Naturaleza. En este curso de 4º de la ESO se trataría de plantearla como una actividad de ampliación.

Del mismo modo,  y relacionado con lo anterior, debe ser incluída en Física de 2º de Bachillerato, como actividad de refuerzo, por su interés en el tema de CAMPO GRAVITATORIO, en lo que respecta a la GRAVITACIÓN EN EL UNIVERSO, dentro del MOVIMIENTO DE SATÉLITES y relacionado con LA TERCERA LEY DE KEPLER.

En esta última versión, se incluye un enlace interesante a un simulador del movimiento de satélites, e incluso del movimiento de la Tierra respecto del Sol e incluso más, que acerca visualmente el contenido:

https://www.eafit.edu.co/ninos/reddelaspreguntas/Paginas/como-se-sostienen-los-satelites.aspx

Animamos a realizar las actividades finales, números 14 y 15 del documento que se adjunta «DE CIRCULAR A KEPLER»,  que puede resultar curiosa la reflexión a la que conducen, sobre todo la actividad número 15, por reflejar una situación imposible.

ASPECTOS FORMALES PARA DOCENTES AL FINAL DEL ARTÍCULO, para no interferir con lo que es de interés para el aprendizaje del alumnado.

EJERCICIO DE GRAVITACIÓN EN EL UNIVERSO PROPUESTO, EJERCICIO F2BE2065:

Una nave realiza una órbita a 99 km de altura sobre la superficie de Hermione, un pequeño planeta de la constelación Potter. El periodo de la nave en su órbita es de 120 minutos.

a.- Hallar la masa de Hermione.

b.- Hallar el campo gravitatorio en la superficie de Hermione.

c.- La velocidad orbital de la nave.

d.- La velocidad que debe tener un cohete de 3 toneladas de masa, para que escape de la superficie de Hermione.

DATOS: G=6.67×10-11 Nm2kg-2 ; RHERMIONE=1750 km; VESFERA=4/3 π·R3 ;1 ton=1000 kg

IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/wMap4o8RJbU

EJERCICIO F2BE2066:

Con los datos que se suministran, hallar la altura de la órbita geoestacionaria, partiendo de la segunda Ley de Newton y de la Ley de Gravitación Universal, considerando las características del movimiento, supuesto Circular Uniforme.

DATOS: G=6.67×10-11 Nm2kg-2.; RT=6370 km; MT=5.98×1024 kg.

IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/D86VXOkxfk4

EJERCICIO F2BE2098:

Determinar la velocidad con la que hay que lanzar un cuerpo desde la superficie de la Tierra para colocarlo en una órbita circular de radio R=20000 km.

Datos: G=6,67·10-11 Nm2kg-2; MTierra=5,97·1024 kg; RTierra=6370 km.

NOTA: El ejercicio se resuelve de dos maneras: una de ellas interpretando que sólo tenemos que colocarlo en la órbita, en esa posición, sin velocidad. La otra forma, quizás sea la más apropiada, llevándolo a la órbita con la energía cinética suficiente para que se quede orbitando, con la velocidad orbital correspondiente. El video lo resuelve de las dos maneras. En cualquier caso, indicar en el ejercicio si cae en examen, la interpretación que se ha hecho del enunciado.

IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/cOjUj6TD9II

EJERCICIO FQ1BE2173:

Copernicus es un programa de Observación de la Tierra de la Unión Europea, que dispone de al menos 6 satélites Sentinel. De hecho actualmente el programa aporta datos de la erupción del volcán Cumbre Vieja en La Palma.

Supongamos que uno de esos satélites Sentinel está en órbita alrededor de la tierra tardando tres horas en dar una vuelta completa al planeta. En esta situación y con los datos que se aportan, hallar:

a.- La altura sobre la superficie de la Tierra a la que se encuentra el satélite.

b.- La velocidad orbital que lleva.

c.- El valor de la aceleración de la gravedad a esa altura.

DATOS: G=6.67×10-11 Nm2kg-2.; RT=6370 km; MT=5.98×1024 kg.

IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/GipAoc-PQAc

LA RESOLUCIÓN DEL EJERCICIO PASO A PASO, EN FORMATO TEXTO, PARA FAVORECER LA INMEDIATEZ DE LA COMPROBACIÓN, LA PUEDE ENCONTRAR EN EL SIGUIENTE ARTÍCULO: EXAMEN FÍSICA 2º BACHILLERATO: GRAVITATORIO, ELECTROMAGNÉTICO, ONDAS Y ÓPTICA

EJERCICIO FQ4EE2676:

La Agencia Espacial de Guanarteme, en Noviembre de 2023, ha descubierto un nuevo planeta, que han denominado “Arretranco” en honor a los acontecimientos y decisiones de los últimos tiempos. Al explorador espacial enviado por la agencia, se le ha encomendado la obtención del valor de la gravedad en la superficie del planeta.

Como consecuencia el astronauta deja caer un destornillador desde la ventana de su nave, a 22 metros sobre el suelo de Arretranco y observa que impacta con el suelo a una velocidad de 13 m/s.

a.- Ayudarle a obtener la gravedad en la superficie de Arretranco.

b.- ¿Podrá con esa experiencia obtener el valor de la masa y el radio de Arretranco?

DATO: G= 6,67·10-11 N/m2·kg2

VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/WFdYQTjV6jY

EJERCICIO FQ1BE2678:

Para un planeta aislado, recientemente descubierto, de masa MP=3,9·1024 kg y de 6000 km de radio, responder a las siguientes cuestiones de interés:

a.- Hallar el valor de la gravedad en la superficie del planeta.

b.- Hallar el tiempo que tarda en dar una vuelta completa un satélite que orbita alrededor del planeta a una altura de 23000 km sobre su superficie.

c.- Hallar la velocidad del satélite en su órbita.

d.- Hallar la aceleración del satélite en su órbita.

e.- Dejamos caer un martillo de 4 kg desde una altura de 20 metros sobre la superficie del planeta. Hallar la velocidad con la que llega al suelo y compararla haciendo los comentarios apropiados con la que llegaría al suelo si la misma experiencia se realizara sobre la superficie de la Tierra.

DATOS: G=6,67·10-11 u.S.I.; gSUPERFICIE TERRESTRE = 9,8 m/s2

IR A LA SOLUCIÓN DEL EJERCICIO

EJERCICIO F2BE2922:

Hallar la altura a la que se encuentra un satélite que tarda dos días en dar una vuelta completa a la Tierra, obteniendo la expresión que permite su cálculo y nombrándola.

Datos: G = 6,67·10–11 N·m2 ·kg-2 ; MT = 5,98·1024  kg; RT = 6370 km;

IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE APLICACIÓN DE LA TERCERA LEY DE KEPLER: EXAMEN RESUELTO PARA FÍSICA DE 2º DE BACHILLERATO. MOVIMIENTO ARMÓNICO SIMPLE, GRAVITACIÓN Y ELECTROMAGNETISMO. SEGUNDO TRIMESTRE CURSO 2024-25

EJERCICIO FQ1BE2850:

Un satélite destinado al estudio del cambio climático en la Tierra, se quiere que tenga un periodo de 2 días.

a.- Obtener la 3ª Ley de Kepler, con todo lujo de detalles, haciendo los razonamientos con rigor, indicando las Leyes utilizadas y las aproximaciones que se consideran.

SOLUCIÓN DE ESTE APARTADO: OBTENCIÓN DE LA TERCERA LEY DE KEPLER

b.- Hallar la altura a la que hay que colocar el satélite.

c.- Hallar el radio de la órbita del satélite.

d.- Hallar la velocidad del satélite, de dos modos diferentes.

e.- Hallar la aceleración del satélite en su órbita y el valor de la gravedad a esa altura.

DATO: G=6.67·10-11 u.S.I.; RT = 6370 km; MT = 5.98·1024 kg

IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN RESUELTO DE GRAVITACIÓN, FUERZAS GRAVITATORIAS Y MOVIMIENTO CIRCULAR UNIFORME, PARA FÍSICA Y QUÍMICA DE 1º DE BACHILLERATO

EJERCICIO FQ1BE2401:

Miranda, con 472 km de diámetro, es el más pequeño de los 5 satélites de Urano. En este satélite se encuentra el que se considera el acantilado más alto del Sistema Solar, el Verona Ropes de 20 km de alto.

Es tan alto, que si te dejaras caer desde el borde tardarías 12 minutos en llegar a la base y lo harías con una velocidad de 200 km/h. Todo ello a pesar de la baja aceleración de la gravedad en el satélite y que no tiene atmósfera. A efectos prácticos podemos suponer que durante toda esta caída libre la aceleración de la gravedad debida a Miranda, se mantiene constante.

Teniendo en cuenta como datos lo mencionado y el valor de G=6.67·10-11 u.S.I., y considerando a Miranda el único astro del Universo hallar (redondeando tanto en los procesos intermedios como en los resultados finales a la milésima):

a.- El valor de la aceleración de la gravedad en la superficie de Miranda.

b.- La masa de Miranda.

EJERCICIO FQ1BE2641:

Hallar la gravedad en la Tierra y la gravedad en la Luna.

Por gravedad entendemos g, la aceleración de la gravedad en un lugar determinado, el campo gravitatorio en un lugar determinado, que corresponde a la fuerza gravitatoria por unidad de masa que se sufre en ese punto en concreto.

Hallar tu peso en la Tierra y tu peso en la Luna.

DATOS: G=6.67·10-11 Nm2kg-2.; RT=6370 km; MT=5.98·1024 kg; RL=1738 km; ML=7.35·1022 kg

EJERCICIO FQ1BE2642:

Teniendo en cuenta la distancia de la Tierra al Sol, y su periodo alrededor del mismo; sabiendo que la distancia de Marte al Sol (228 millones de km) y que su periodo es de 1,88 años terrestres, comprobar la tercera ley de Kepler.

Esto es, hallar el valor de k para el movimiento de la Tierra y el de k para el movimiento de Marte y contrastar los resultados obtenidos.

Una vez hallada este valor de k y conociendo el valor de G, comprobar el valor obtenido para la masa del Sol.

EJERCICIO FQ1BE2643:

Actualmente existen alrededor de 18 000 objetos artificiales orbitando alrededor del planeta Tierra, muchos de ellos son satélites operativos, pero la mayoría son basura espacial generada principalmente por Rusia, Estados Unidos y China.

La basura espacial es un tema de preocupación que sin duda comenzará pronto a tomar importancia.

Pese al pequeño tamaño de la mayor parte de los fragmentos, las vertiginosas velocidades a las que están sometidas, hacen de éstos una seria amenaza a cualquier misión que pueda ser efectuada en un futuro próximo.

Desde 1991, se han registrado al menos tres colisiones en la órbita terrestre por culpa de la basura espacial. Estas colisiones se irán multiplicando y, a la vez, aumentarán los objetos peligrosos en órbita.

Imagina un trozo de basura espacial que se encuentra a 37000 km de altura de la Tierra. Hallar la velocidad que debe tener para mantenerse en órbita sobre la Tierra.

DATOS: G=6.67·10-11 Nm2kg-2.; RT=6370 km; MT=5.98·1024 kg.

EJERCICIO FQ1BE2644:

Los satélites geoestacionarios son aquellos que realizan órbitas sobre el Ecuador Terrestre a la velocidad a la que gira la Tierra.

El objetivo es permanecer encima del mismo punto del planeta. El primer satélite geoestacionario fue el Syncom 3, el cual fue lanzado desde el Campo Kennedy en 1964. El lanzamiento de este satélite experimental permitió probar comunicaciones y cubrió los Juegos Olímpicos de 1964 en Tokio para la televisión en vivo.

Hallar la altura de la órbita geoestacionaria.

DATOS: G=6.67·10-11 Nm2kg-2.; RT=6370 km; MT=5.98·1024 kg.

EJERCICIO F2BE2691:

a.- Obtener la altura de la órbita geoestacionaria, haciendo con rigor todos los desarrollos y razonamientos necesarios, indicando la utilidad de situar satélites a esa altura.

b.- Hallar la energía total de un satélite de 500 kg orbitando en esa órbita geoestacionaria.

c.- Hallar la energía que hay que comunicarle al satélite del apartado anterior para que pase a otra órbita situada a 40000 km de la superficie de la Tierra.

DATOS: G=6,67·10-11 Nm2kg-2; MTierra=5,97·1024 kg; RTierra=6370 km.

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE GRAVITACIÓN EN EL UNIVERSO

EJERCICIO FQ1BE2645:

El Falcon 9, de la empresa Spacex, que despegará si se cumplen las predicciones el 10 de mayo de 2018, desde el Centro Espacial Kennedy en Florida, tiene una masa de aproximadamente 550 toneladas.

Suponiendo que sus motores desarrollan una fuerza de 45 millones de newton, hallar la aceleración en el momento del despegue.

Si fuera capaz de mantener esa aceleración durante todo el tiempo que dura su ascenso, hallar la velocidad con la que alcanza la órbita geoestacionaria.

EJERCICIO FQ1BE2646:

Un satélite de 900 kg describe una órbita circular de radio 3·RTierra.

a.- Calcular la aceleración del satélite en su órbita
b.- Deduce y calcula la velocidad orbital para dicho satélite

DATOS: G=6.67·10-11 Nm2kg-2.; RT=6370 km; MT=5.98·1024 kg.

EJERCICIO FQ1BE2647:

Un pequeño satélite artificial de 1000 kg de masa, destinado a la detección de incendios, describe una órbita circular alrededor de la Tierra cada 90 minutos. Calcule:

a.- La altura sobre la superficie de la Tierra a la que se encuentra el satélite.

b.- La velocidad y la aceleración del satélite en su órbita.

DATOS: G=6.67·10-11 Nm2kg-2.; RT=6370 km; MT=5.98·1024 kg.

EJERCICIO FQ1BE2648:

Un satélite de 500 kg describe una órbita circular alrededor de la Tierra de radio 2 RT. Calcular:

a.- La fuerza gravitatoria que actúa sobre el satélite

b.- El tiempo que tarda el satélite en dar una vuelta a la Tierra.

c.- Dibujar las fuerzas que actúan sobre el satélite.

DATOS: G=6.67·10-11 Nm2kg-2.; RT=6370 km; MT=5.98·1024 kg.

EJERCICIO FQ1BE2649:

Un satélite de 500 kg de masa se mueve alrededor de Marte, describiendo una órbita circular a 61000 km de su superficie. Sabiendo que la aceleración de la gravedad en la superficie de Marte es 3,7 m/s2 y que su radio es de 3400 km, calcula:

a) Fuerza gravitatoria sobre el satélite.

b) Velocidad y periodo del satélite.

c) ¿A qué altura debería encontrarse el satélite para que su periodo fuese el doble?

DATOS: G=6.67·10-11 Nm2kg-2.

EJERCICIO FQ1BE2650:

Un satélite de 500 kg describe una órbita circular alrededor de la Tierra de radio 2·RT. Calcula:

a.- La Fuerza gravitatoria que actúa sobre el satélite.

b.- El tiempo que tarda el satélite en dar una vuelta a la Tierra.

DATOS: G=6.67·10-11 Nm2kg-2.; RT=6370 km; MT=5.98·1024 kg.

EJERCICIO FQ1BE2651:

Un pequeño planeta de masa 3,0·1024 kg y radio 3000 km tiene un satélite a una altura de 3·105 km sobre la superficie del planeta. El satélite se mueve en una órbita circular con una masa de 200 kg. Calcula:

a.- La aceleración de la gravedad sobre la superficie del planeta.

b.- La fuerza gravitatoria que ejerce el planeta sobre el satélite.

c.- La velocidad del satélite.

DATOS: G=6.67·10-11 Nm2kg-2

EJERCICIO FQ1BE2652:

Un satélite de 500 kg debe recorrer una trayectoria circular a 320 km encima de la superficie de un planeta de 5600 km de radio. La intensidad de campo gravitatorio en dicha superficie es de 6,5 N/Kg. Calcular:

a.- Velocidad del satélite.

b.- Aceleración normal

DATOS: G=6.67·10-11 Nm2kg-2

EJERCICIO FQ1BE2653:

Un meteorito de 400 kg de masa se dirige directo, en caída libre, hacia la Tierra desde
una altura sobre la superficie terrestre h = 500 km. Determinar:

a) El campo gravitatorio a dicha altura h.

b) Dibujar las fuerzas que actúan sobre el meteorito.

c) Hallar la fuerza que actúa sobre el meteorito

DATOS: G=6.67·10-11 Nm2kg-2.; RT=6370 km; MT=5.98·1024 kg.

EJERCICIO FQ1BE2654:

Imaginemos que la Tierra es completamente esférica y que su radio es exactamente 6371 km. Sabiendo que la altura del Everest es de 8848 metros.

Hallar el tiempo que tardaría un satélite hipotético, a una altura al menos 2 metros por encima del Everest para que no se estampe con él, en dar una vuelta completa a la Tierra en esa órbita super ajustada.

DATOS: G=6.67·10-11 Nm2kg-2.; RT=6370 km; MT=5.98·1024 kg.     (SOL: 5073 s)

EJERCICIO FQ1BE2655:

Un pequeño satélite artificial de 1000 kg de masa, destinado entre otras funciones a la detección de poblaciones masivas de fitoplancton, describe una órbita circular alrededor de la Tierra cada hora.

Calcular:

a.- La altura sobre la superficie de la Tierra a la que se encuentra el satélite. Añadir al cálculo de esa altura comentarios relevantes acerca del resultado, que pueden influir en la resolución del apartado b, que se pide a continuación.

b.- La velocidad y la aceleración del satélite en su órbita.

DATOS:  G=6.67·10-11 Nm2kg-2.; RT=6370 km; MT=5.98·1024 kg.

EJERCICIO FQ1BE2656:

Si la Luna se encontrara a 105 km de la Tierra, ¿cuál sería su periodo de revolución alrededor de la misma?. Comparar el resultado con la situación real, que es aproximadamente de 28 días (exactamente de 27,3 días).

DATOS: G=6.67·10-11 Nm2kg-2.; RT=6370 km; MT=5.98·1024 kg.; distancia real (Tierra-Luna)=384000 km; go=9,81 N/kg.

SOLUC:  1,44 horas

EJERCICIO FQ1BE2657:

El período orbital de la Luna es de 28 días terrestres y el radio de su órbita, supuesta circular, vale 384 000 km. Con esos datos, calcula la masa terrestre, sabiendo que el valor de la constante de gravitación universal es: G=6.67·10-11 Nm2kg-2

SOLUC: 5,73·1024 kg

EJERCICIO FQ1BE2658:

Se acaban de descubrir tres nuevos planetas, de los que se conocen los siguientes datos:

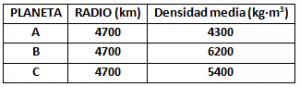
Indica en cuál de los tres planetas A, B o C, será superior el peso de un mismo cuerpo.

EJERCICIO FQ1BE2659:

Dos masas m y m’ están separadas una distancia R. Si las aproximamos hasta una distancia de la décima parte de R, el módulo de la fuerza gravitatoria que actúa entre ellas:

a) Dismimuye 100 veces.

b) Dismimuye 10 veces.

c) Aumenta 10 veces.

d) Aumenta 100 veces.

e) Ni aumenta ni disminuye.

f) Ninguna respuesta de las anteriores es correcta.

Elegir la respuesta correcta, trabajando con todo el rigor posible y razonando profundamente el resultado, acompañando de las Leyes que justifiquen el resultado.

IR A LA RESOLUCIÓN DETALLADA DE ESTE EJERCICIO / CUESTIÓN: EJERCICIO RESUELTO / CUESTIÓN DE RAZONAMIENTO CON LA LEY DE GRAVITACIÓN UNIVERSAL PARA FÍSICA DE BACHILLERATO

EJERCICIO FQ1BE2660:

Un satélite de 500 kg de masa se mueve alrededor de Marte, describiendo una órbita circular a 61000 km de su superficie. Sabiendo que la aceleración de la gravedad en la superficie de Marte es 3,7 m/s2 y que su radio es de 3400 km, calcula:

a) Fuerza gravitatoria sobre el satélite.

b) Velocidad y periodo del satélite (en días horas minutos y segundos).

c) ¿A qué altura debería encontrarse el satélite para que su periodo fuese el doble?

SOLUCIONES: 5,16 N; 815,23 m/s; 5 días, 17 horas, 52 minutos, 48 s; 9,86·107 m

EJERCICIO FQ1BE2661:

Un pequeño planeta de masa 3,0·1024 kg y radio 3000 km tiene un satélite a una altura de 3·105 km sobre la superficie del planeta. El satélite se mueve en una órbita circular con una masa de 200 kg. Calcula:

a) La aceleración de la gravedad sobre la superficie del planeta.

b) La fuerza gravitatoria que ejerce el planeta sobre el satélite.

c) La velocidad del satélite.

DATOS: G=6.67·10-11 Nm2kg-2.; RT=6370 km; MT=5.98·1024 kg.

Soluc: 22,23 N/m; 0,43 N; 812,65 m/s.

EJERCICIO FQ1BE2662:

¿A qué distancia del centro terrestre está el punto donde se compensan la gravedad lunar y la terrestre, si la masa de la Luna es 0,012 veces la masa de la Tierra?

Distancia Tierra-Luna = 384000 km

Soluc: 346088 km

EJERCICIO FQ1BE2663:

Fobos es un satélite de Marte que gira en una órbita circular de radio 9380 km con un periodo de revolución de 7.65 h. Deimos, otro satélite de Marte, gira en otra órbita circular de radio 23460 km. Determine:

a) La masa de Marte.

b) El periodo de revolución del satélite Deimos.

Datos: G=6.67·10-11 Nm2kg-2; MF=1.1·1016 kg; MD=2.4·1015 kg

SOLUC: 6,4·1025 kg; 30,26 dias

EJERCICIO FQ1BE2664:

Un satélite de 10.000 kg orbita alrededor de la tierra a una velocidad de 4.2 km/s. Con los datos proporcionados calcular:

a) Radio de la órbita.

b) Tiempo en dar 10 vueltas.

c) Energía potencial gravitatoria del satélite (sólo para alumnos de 2º de Bachillerato).

DATOS: G=6.67·10-11 Nm2kg-2.; RT=6370 km; MT=5.98·1024 kg.

SOLUC.: 2,26·107 m; 3,38·105 s

EJERCICIO FQ1BE2665:

Un satélite de 1000 kg se encuentra orbitando alrededor de la tierra a una altura de 300 km. Si sabemos que el radio de la tierra es de 6370 km y que la gravedad es de 9.8 m/s2, calcular:

a) Velocidad lineal del satélite

b) Aceleración del satélite en la órbita

c) Periodo

d) Trabajo para poner el satélite en órbita (sólo para alumnos de 2º de Bachillerato).

SOLUC.: 7721,28 m/s; 8,94 m/s2; 5427,71 s

EJERCICIO F1BE2671:

Un Astronauta en el planeta Mencey, que será próximamente colonizado, deja caer desde lo alto de su nave de 58 m de alto, “amenceyada” (aterrizada si fuera en la Tierra) en su superficie, un martillo de 2,5 kg de masa, que impacta contra el suelo con una velocidad de 90 km/h, según indica el detector de velocidades de la base de la nave.

Una sonda espacial, enviada meses antes de la llegada de este astronauta indicó que el planeta Mencey tiene un diámetro de 4230 km.

Con los datos que se suministran y teniendo en cuenta que la Constante de Gravitación Universal tiene un valor de 6,67·10-11 en unidades del S.I., responder a las siguientes cuestiones:

a.- Hallar el tiempo que tarda el martillo en llegar al suelo.

b.- Hallar el valor de la gravedad en la superficie del planeta.

c.- Hallar la masa del planeta Mencey.

d.- Obtener las unidades en el Sistema Internacional de la Constante de Gravitación Universal, partiendo de la Ley de Gravitación Universal.

e.- Hallar el valor de la velocidad de un satélite que orbitando alrededor de Mencey tarda 15 horas en completar una vuelta.

ALTERNATIVA DE CONTINUACIÓN PARA ESTE APARTADO EXCLUSIVAMENTE: Si no has sido capaz de obtener la masa del planeta en los apartados anteriores, utilizar el valor de MMENCEY = 4,5·1024 kg, (indicarlo claramente en ese caso).

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO

EJERCICIO F1BE2672:

Un senderista en el planeta Guayre, recientemente colonizado y curiosamente con una masa similar a la de la Tierra, observa que como consecuencia de un guayrremoto (terremoto si ocurriera en la Tierra) una roca de 250 kg llega al suelo desde el borde de un risco a una altura de 80 metros, con una velocidad de 120 km/h.

Con los datos que se suministran y teniendo en cuenta que el valor de la Constante de Gravitación Universal tiene un valor de 6,67·10-11 en unidades del S.I., responder a las siguientes cuestiones:

a.- Hallar el tiempo que tarda la roca en llegar al suelo.

b.- Hallar la aceleración de la gravedad en la superficie de Guayre.

c.- Hallar el radio del planeta Guayre.

d.- Explicar razonadamente y con todo lujo de detalles, al amparo de los resultados obtenidos, cuál de los dos planetas, Tierra o Guayre, tiene mayor densidad.

ALTERNATIVA DE CONTINUACIÓN: Caso que no hayas sido capaz de obtener el Radio con la realidad de los apartados anteriores, utilizar exclusivamente en este apartado y el siguiente el dato RGUAYRE = 8000 km (indicarlo claramente en ese caso).

e.- Hallar el tiempo que tarda en dar una vuelta completa un satélite que orbita alrededor de Guayre a una altura de 790 km. Indicarlo en ____horas, ____ minutos,____segundos.

DATOS: MGUAYRE = 5,8·1024 kg; gTIERRA = 9,8 N/kg; RTIERRA = 6370 km

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE GRAVITACIÓN

 

PUEDE SER DE INTERÉS EL SIGUIENTE DOCUMENTO, DE RECOPILACIÓN DE CONTENIDOS:

15 P438 DE CIRCULAR A KEPLER V17 V1

ASPECTOS FORMALES PARA DOCENTES:

SE PRETENDE CON ESTA DINÁMICA EL DESARROLLO DE LAS COMPETENCIAS:

RELACIONADO CON LOS SABERES BÁSICOS DE FÍSICA Y QUÍMICA:

SE CONTEMPLAN LOS ASPECTOS RELACIONADOS CON EL PERFIL DE SALIDA DEL ALUMNADO DE LOS INSTITUTOS DIOCESANOS DE CANARIAS

PODRÍA INTERESAR LA VISITA AL SIGUIENTE ARTÍCULO DEL PROYECTO, DONDE SE DESARROLLAN LAS ASIGNATURAS DE FÍSICA Y QUÍMICA DE SECUNDARIA Y BACHILLERATO:

Post Views: 5.231
On:

Comments are closed, but trackbacks and pingbacks are open.