GRAVITACIÓN UNIVERSO. LEYES DE KEPLER. SATÉLITES

GRAVITACIÓN UNIVERSO KEPLER SATÉLITES

GRAVITACIÓN EN EL UNIVERSO, MOVIMIENTO DE SATÉLITES, UTILIZACIÓN DE LAS LEYES DE KEPLER:

Este es un contenido que si bien se introduce en Física y Química de 1º de Bachillerato, se trata en profundidad en Física de 2º de Bachillerato.

INTERESA LA CONSULTA DEL ARTÍCULO: LEY DE GRAVITACIÓN UNIVERSAL

CONTENIDOS TEÓRICOS DE INTERÉS:

TERCERA LEY DE KEPLER:

Cualquier astro que orbite alrededor de otro (como cualquiera de los planetas del Sistema Solar alrededor del Sol), incluso satélites naturales o no que orbiten alrededor de un planeta, si suponemos que la única fuerza presente es la fuerza gravitatoria y que el movimiento que se produce es circular y uniforme, se cumple, utilizando la 2ª Ley de Newton y la Ley de Gravitación Universal:

Teniendo en cuenta que la velocidad (que la obtenida es la velocidad orbital), SUPONIENDO EL MOVIMIENTO UNIFORME, es igual al espacio entre el tiempo; que el espacio es la longitud de la circunferencia y el tiempo que tarda en recorrerla se denomina periodo:

LLegamos a la expresión de la Tercera Ley de Kepler, que relaciona el radio de la órbita, con el tiempo que se tarda en recorrerla.

VELOCIDAD ORBITAL:

La velocidad que se tiene que llevar en una órbita, para mantenerse orbitando, tiene que ser tangente a la trayectoria supuesta circular. Aplicando la 2ª Ley de Newton al movimiento del satélite, supuesto circular y uniforme (sólo tiene aceleración normal).

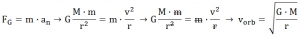
ENERGÍA MECÁNICA DEL SATÉLITE QUE ESTÁ ORBITANDO:

Al ser el campo gravitatorio un campo conservativo, la energía que tendrá el satélite en su órbita viene dada por la expresión de la energía mecánica (suma de las energías cinética y potencial).

Si ponemos el resultado de la VELOCIDAD ORBITAL, en la expresión de la energía cinética, puesto que el satélite está en órbita, obtenemos para la energía mecánica:

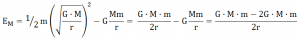
Que podemos notar que coincide con la mitad de la energía potencial, para un satélite que se mantiene en órbita.

ENERGÍA PARA PONER UN SATÉLITE EN ÓRBITA:

Es la energía que se necesita transmitir al satélite para ponerlo en órbita. Se determina aplicando el principio de conservación de la energía mecánica comparando la posición inicial sobre la superficie de la Tierra(R_T), otro planeta o cualquier posición inicial y la posición final a la altura de la órbita. Teniendo en cuenta que el campo gravitatorio es conservativo y considerando despreciables los posibles rozamientos con la atmósfera (por ejemplo):

Si el satélite parte de la superficie de la Tierra (por ejemplo), ya tiene una cierta Ep. Se trataría de obtener la energía cinética del lanzamiento. Con esta expresión podemos calcular además la velocidad del lanzamiento necesaria.

CÁLCULO DE LA ENERGÍA DE UN SATÉLITE PARA PASAR DE UNA ÓRBITA A OTRA:

La energía que tenemos que comunicar a un satélite para que pase de una órbita 1 a otra órbita 2, será la diferencia de las energías que tiene (o tendrá) en cada una de las órbitas.

Si queremos que pase de la órbita 1 a la órbita 2:

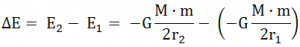
- - - Notar que la energía es la energía mecánica en la órbita, desarrollado en el apartado anterior de la VELOCIDAD ORBITAL.
    - Si la variación de energía es positiva, hay que comunicarle energía al satélite para que cambie de órbita, que es lo que hay que hacer si queremos una órbita más alejada (de la Tierra por ejemplo).

VELOCIDAD DE ESCAPE:

Para que un satélite escape del campo gravitatorio en la posición en la que se encuentra su energía mecánica tiene que igual a cero (o mayor que cero). Considerado de otra forma: su energía cinética tiene que compensar la energía potencial que posee (que es reflejo de la atracción gravitatoria que sufre el satélite en esa posición).

La velocidad de escape sería la mínima velocidad que se debe suministrar a un cuerpo para que escape definitivamente de un cuerpo celeste (planeta, satélite…), poniéndolo a una distancia infinita del que se pretende escapar. Si suponemos que no hay rozamiento, aplicamos el principio de conservación de la energía mecánica entre el cuerpo y el infinito, teniendo en cuenta que la energía mecánica en el infinito sería cero:

E_A = E_∞

(E_c + E_p)_A = (E_c + E_p)_∞

(E_c + E_p)_A = 0

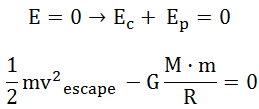
ENERGÍA PARA ESCAPAR DE UNA ÓRBITA CONCRETA:

Al igual que con la velocidad de escape anterior, un satélite orbitando escapará de la atracción gravitatoria cuando le comuniquemos una energía que cumpla:

E_órbita + E_comunicamos = 0

La energía en la órbita, corresponde a la energía mecánica y la que tendremos que comunicar debe compensar la anterior. Al poner igual a cero, vamos a obtener la energía mínima para que escape.

Proponemos el siguiente ejercicio que se resuelve en el vídeo que se mostrará con posterioridad al enunciado. El alumno debe intentar resolverlo antes de ver el vídeo.

EJERCICIO DE GRAVITACIÓN EN EL UNIVERSO PROPUESTO, EJERCICIO F2BE2065:

Una nave realiza una órbita a 99 km de altura sobre la superficie de Hermione, un pequeño planeta de la constelación Potter. El periodo de la nave en su órbita es de 120 minutos.

a.- Hallar la masa de Hermione.

b.- Hallar el campo gravitatorio en la superficie de Hermione.

c.- La velocidad orbital de la nave.

d.- La velocidad que debe tener un cohete de 3 toneladas de masa, para que escape de la superficie de Hermione.

DATOS: G=6.67×10^-11 Nm²kg^-2 ; R_HERMIONE=1750 km; V_ESFERA=4/3 π·R³ ;1 ton=1000 kg

Al vídeo que resuelve el ejercicio, con algunas propuestas de desarrollos iniciales de los procesos, que desde las principales leyes físicas, nos conducen a la fórmula final que resuelve cada uno de los apartados, se llega con el siguiente enlace: https://youtu.be/wMap4o8RJbU

Añadimos aclaraciones a los aspectos en los que los alumnos pueden cometer errores.

EJERCICIO F2BE2066:

Con los datos que se suministran, hallar la altura de la órbita geoestacionaria, partiendo de la segunda Ley de Newton y de la Ley de Gravitación Universal, considerando las características del movimiento, supuesto Circular Uniforme.

DATOS: G=6.67×10^-11 Nm²kg^-2.; R_T=6370 km; M_T=5.98×10²⁴ kg.

VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/D86VXOkxfk4

EJERCICIO F2BE2098:

Determinar la velocidad con la que hay que lanzar un cuerpo desde la superficie de la Tierra para colocarlo en una órbita circular de radio R=20000 km.

Datos: G=6,67·10^-11 Nm²kg^-2; M_Tierra=5,97·10²⁴ kg; R_Tierra=6370 km.

NOTA: El ejercicio se resuelve de dos maneras: una de ellas interpretando que sólo tenemos que colocarlo en la órbita, en esa posición, sin velocidad. La otra forma, quizás sea la más apropiada, llevándolo a la órbita con la energía cinética suficiente para que se quede orbitando, con la velocidad orbital correspondiente. El video lo resuelve de las dos maneras. En cualquier caso, indicar en el ejercicio si cae en examen, la interpretación que se ha hecho del enunciado.

VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/cOjUj6TD9II

EJERCICIO FQ1BE2173:

Copernicus es un programa de Observación de la Tierra de la Unión Europea, que dispone de al menos 6 satélites Sentinel. De hecho actualmente el programa aporta datos de la erupción del volcán Cumbre Vieja en La Palma.

Supongamos que uno de esos satélites Sentinel está en órbita alrededor de la tierra tardando tres horas en dar una vuelta completa al planeta. En esta situación y con los datos que se aportan, hallar:

a.- La altura sobre la superficie de la Tierra a la que se encuentra el satélite.

b.- La velocidad orbital que lleva.

c.- El valor de la aceleración de la gravedad a esa altura.

DATOS: G=6.67×10^-11 Nm²kg-².; R_T=6370 km; M_T=5.98×10²⁴ kg.

VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/GipAoc-PQAc

LA RESOLUCIÓN DEL EJERCICIO PASO A PASO, EN FORMATO TEXTO, PARA FAVORECER LA INMEDIATEZ DE LA COMPROBACIÓN, LA PUEDE ENCONTRAR EN EL SIGUIENTE ARTÍCULO: EXAMEN FÍSICA 2º BACHILLERATO: GRAVITATORIO, ELECTROMAGNÉTICO, ONDAS Y ÓPTICA

EJERCICIO F2BE2691:

a.- Obtener la altura de la órbita geoestacionaria, haciendo con rigor todos los desarrollos y razonamientos necesarios, indicando la utilidad de situar satélites a esa altura.

b.- Hallar la energía total de un satélite de 500 kg orbitando en esa órbita geoestacionaria.

c.- Hallar la energía que hay que comunicarle al satélite del apartado anterior para que pase a otra órbita situada a 40000 km de la superficie de la Tierra.

DATOS: G=6,67·10^-11 Nm²kg^-2; M_Tierra=5,97·10²⁴ kg; R_Tierra=6370 km.

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE GRAVITACIÓN EN EL UNIVERSO

EJERCICIO F2BE2843:

Un satélite meteorológico tiene una masa de 1070 kg y se encuentra en la actualidad a una altura de 36000 km por encima del ecuador describiendo una órbita circular en torno a la Tierra. Calcule: (8 puntos)

a.- La velocidad del satélite en su órbita, obteniendo la expresión haciendo los razonamientos apropiados.

b.- La energía del satélite en su órbita.

c.- La aceleración (obtenerla de dos modos diferentes) y el peso del satélite en su órbita, dibujando e indicando las fuerzas que actúan sobre el satélite.

d.- La pérdida de energía del satélite, si después de unos años en funcionamiento, se encontrase a una altura de 35426 km en una nueva órbita.

e.- El periodo del satélite en la órbita inicial (36000 km) en horas, obteniendo la expresión que permite su cálculo y haciendo comentarios al resultado obtenido.

f.- El periodo del satélite en la órbita final (35426 km) en horas, haciendo comentarios al resultado obtenido.

g.- La velocidad del satélite en la órbita final, (de dos formas diferentes).

h.- Indicar las unidades de la Constante de Gravitación Universal en el Sistema Internacional, obteniéndolas de forma razonada a través de la Ley de Gravitación Universal, que debe enunciarse.

Datos: G = 6,67·10 ^-11U.S.I.; M_TIERRA = 5,98·10²⁴ kg; R_TIERRA = 6370 km

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN RESUELTO DE FÍSICA DE 2º DE BACHILLERATO. CURSO 2024-25. PRIMER TRIMESTRE. CAMPO GRAVITATORIO Y GRAVITACIÓN

EJERCICIO FQ1BE2850:

Un satélite destinado al estudio del cambio climático en la Tierra, se quiere que tenga un periodo de 2 días.

a.- Obtener la 3ª Ley de Kepler, con todo lujo de detalles, haciendo los razonamientos con rigor, indicando las Leyes utilizadas y las aproximaciones que se consideran.

SOLUCIÓN DE ESTE APARTADO: OBTENCIÓN DE LA TERCERA LEY DE KEPLER

b.- Hallar la altura a la que hay que colocar el satélite.

c.- Hallar el radio de la órbita del satélite.

d.- Hallar la velocidad del satélite, de dos modos diferentes.

e.- Hallar la aceleración del satélite en su órbita y el valor de la gravedad a esa altura.

DATO: G=6.67·10^-11 u.S.I.; R_T= 6370 km; M_T= 5.98·10²⁴ kg

IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN RESUELTO DE GRAVITACIÓN, FUERZAS GRAVITATORIAS Y MOVIMIENTO CIRCULAR UNIFORME, PARA FÍSICA Y QUÍMICA DE 1º DE BACHILLERATO

EJERCICIO F2BE2347:

En el planeta Mashangou, recientemente colonizado por su interés minero, el valor de la aceleración de la gravedad en su superficie es de 11,3 N/kg.

La federación interplanetaria que ha colonizado el planeta ha conseguido poner un satélite mashango-estacionario, modelo Sopladera 15, de 3500 kg de masa, a una altura sobre su superficie de 40000 km.

a.- Hallar la masa del planeta.

b.- Hallar el periodo de rotación del planeta, en horas, indicando los razonamientos necesarios para su obtención a través de la 2ª Ley de Newton, aproximación de movimiento circular uniforme, 3ª Ley de Kepler…

c.- Hallar la velocidad orbital del satélite en la órbita mashango-estacionaria.

d.- Hallar la energía mecánica del satélite en su órbita mashango-estacionaria.

Recordar que todo debe razonarse, en el sentido de que si se utiliza una única expresión para esta energía mecánica en órbita, debe obtenerse a partir de las energías implicadas y las reflexiones correspondientes.

e.- Hallar la energía mecánica del satélite en una nueva órbita 5000 km por encima de la órbita mashango-estacionaria.

f.- Hallar la velocidad en esa nueva órbita.

g.- Hallar el trabajo que realizan las fuerzas del campo gravitatorio para colocar el satélite en esa órbita 5000 km por encima de la mashango-estacionaria, interpretando el signo del trabajo con todo el rigor posible.

h.- Hallar el trabajo que realizan posteriormente las fuerzas del campo gravitatorio para devolver al Sopladera 15 a su órbita estacionaria desde la órbita 5000 km por encima, interpretando el signo del trabajo con todo el rigor posible.

i.- Hallar el trabajo que han realizado las fuerzas gravitatorias en el recorrido completo que va desde la órbita estacionaria a la de 5000 km por encima y vuelta a la órbita estacionaria. Interpretar el sorprendente resultado con todo lujo de detalles y rigor.

j.- Hallar la energía que hay que suministrarle al satélite para que pase de la órbita estacionaria a la de 5000 km por encima de ella, justificando el signo obtenido y atreviéndose a proponer la estrategia que seguirá el satélite para el cambio de órbita.

k.- Hallar la energía que hay que suministrarle al satélite para que pase de la órbita de 5000 km encima de la estacionaria a la estacionaria, justificando el signo obtenido y atreviéndose a proponer la estrategia que seguirá el satélite para el cambio de órbita.

l.- Un meteorito de elevadas dimensiones y de 20000 kg de masa se aproxima peligrosamente al planeta. Cuando se encuentra a 30000 km de su superficie su velocidad es de 500 km/h. Indicar la energía mecánica del meteorito.

m.- Con la realidad planteada en el apartado anterior y suponiendo que no existe atmósfera en el planeta que implique rozamiento por fricción del meteorito con el aire, hallar la velocidad de impacto del meteorito en la superficie del planeta.

n.- Dibujar y obtener el valor de la aceleración del satélite en su órbita estacionaria.

ñ.- Dibujar y obtener el valor del campo gravitatorio que afecta al satélite en su órbita estacionaria.

o.- Dibujar y obtener el valor de la fuerza gravitatoria que sufre el satélite en su órbita geoestacionaria.

p.- Hallar la velocidad de escape del satélite desde la superficie del planeta, indicando los razonamientos necesarios para su obtención.

DATOS: G=6.67·10^-11 N·m²·kg-².; R_PLANETA=9240 km.

SOLUCIONES ?: a) 1.45E25 kg; b) 19.37 horas; c) 4433 m/s; d) -3.44E10 J; e) -3.12E10 J; f) 4222,67 J; g) -6.3E9 J; h) 6.3E9 J; i) O J; j) 3.2E9 J (en elaboración)

CUESTIÓN F2BE2814:

Un satélite artificial de 500 kg de masa es lanzado desde la superficie terrestre y se sitúa en una órbita circular a una altura de 1200 km. Determine la velocidad del satélite cuando se encuentra en dicha órbita.

Datos: G= 6,67·10^–11N·m² ·kg^–2; M_T= 5,98·10²⁴ kg; R_T= 6370 km.

INTERESA PARA ESTE APARTADO LA CONSULTA DEL SIGUIENTE CONTENIDO TEÓRICO: VELOCIDAD ORBITAL

IR A LA SOLUCIÓN DE ESTA PREGUNTA: CUESTIÓN RESUELTA F2BE2814, DE EXAMEN PAU/EBAU DE FÍSICA DE 2º BACHILLERATO. JUNIO 2024. GRAVITACIÓN EN EL UNIVERSO

EJERCICIO F2BE2815:

Un fragmento de basura espacial de 400 kg de masa, se mueve directo hacia el centro de la Tierra, en caída libre, bajo la acción de su campo gravitatorio. Su velocidad es de 2300 m/s cuando se encuentra a 200 km sobre la superficie terrestre. Calcule:

a) Las energías cinética y potencial que tendrá el objeto a la altura mencionada anteriormente.

b) La altura inicial sobre la superficie de la Tierra desde la que comenzó a caer este objeto, si su velocidad a dicha altura era nula. ¿A qué aceleración estaría sometido ese objeto en ese punto de partida?

c) La velocidad y la aceleración con la que impactará el objeto en la superficie de la Tierra.

Datos: G= 6,67·10^–11 N·m² ·kg^–2; M_T= 5,98·10²⁴ kg; R_T= 6370 km.

IR A LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EJERCICIO RESUELTO F2BE2815. FÍSICA 2º BACHILLERATO. GRAVITACIÓN. EXAMEN EBAU / PAU CANARIAS JUNIO 2024

EJERCICIO F2BE2816:

Sabiendo que la masa de una persona es de 75 kg, y que la distancia de la Tierra a la Luna (de centro a centro) es de 3,84·10⁵ km, calcule:

a) El módulo de la fuerza gravitatoria que ejerce la Luna sobre dicha persona cuando ésta se encuentra sobre la superficie terrestre en el punto más cercano a la Luna.

b) La relación entre dicha fuerza y la ejercida por la Tierra sobre la misma persona.

c) Los valores de la velocidad de escape en las superficies de la Tierra y de la Luna.

INTERESA PARA ESTE APARTADO LA CONSULTA DEL CONTENIDO TEÓRICO: VELOCIDAD DE ESCAPE

Datos: G = 6,67·10^–11 N·m² ·kg^-2 ; M_T = 5,98·10²⁴ kg; R_T = 6370 km; M_L = 7,35·10²² kg; R_L = 1740 km.

IR A LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE GRAVITACIÓN EN EL UNIVERSO: EJERCICIO F2BE2816 RESUELTO PASO A PASO. FÍSICA 2º BACHILLERATO. GRAVITACIÓN. EXAMEN EBAU/PAU JUNIO 2024 CANARIAS

EJERCICIO F2BE2823:

Un pequeño satélite artificial de 200 kg de masa describe una órbita circular alrededor de la Tierra cada 12 horas. Calcule:

a) A qué altura sobre la superficie de la Tierra se encuentra el satélite.

INTERESA PARA ESTE APARTADO LA CONSULTA DEL SIGUIENTE CONTENIDO TEÓRICO: TERCERA LEY DE KEPLER

INTERESA PARA ESTE APARTADO LA CONSULTA DEL SIGUIENTE CONTENIDO TEÓRICO: VELOCIDAD ORBITAL

b) La velocidad y la aceleración del satélite en su órbita.

INTERESA PARA ESTE APARTADO LA CONSULTA DEL CONTENIDO TEÓRICO: VELOCIDAD DE ESCAPE

c) La energía que necesita el satélite para ser transferido a una nueva órbita circular en la que su periodo sea de 24 horas.

INTERESA PARA ESTE APARTADO LA CONSULTA DEL SIGUIENTE CONTENIDO TEÓRICO: ENERGÍA DEL PASO DE UNA ÓRBITA A OTRA NUEVA

Datos: G = 6,67·10^–11 N m² kg^–2; R_T = 6370 km; M_T = 5,98·10²⁴ kg.

IR A LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE GRAVITACIÓN EN EL UNIVERSO: EJERCICIO F2BE2823, RESUELTO PASO A PASO. FÍSICA 2º BACHILLERATO. GRAVITACIÓN. EXAMEN EBAU/PAU JUNIO 2024 CANARIAS

EJERCICIO F2BE2824:

Una sonda espacial de masa m es lanzada verticalmente desde la superficie de un planeta de masa M y radio R.

a) Determine la velocidad mínima con la que debe ser lanzada la sonda para que escape del planeta.

INTERESA PARA ESTE APARTADO LA CONSULTA DEL CONTENIDO TEÓRICO: VELOCIDAD DE ESCAPE

b) Si la sonda espacial es lanzada con una energía cinética de 10¹¹ J, calcule la velocidad de la sonda y el módulo de la fuerza que ejerce el planeta sobre ella en el momento del lanzamiento ¿Escapa la sonda espacial del planeta?

c) Calcule el peso de la sonda y su aceleración, cuando se encuentra una distancia de 700 km sobre la superficie del planeta.

Datos: G = 6,67·10^–11 N m² kg^–2; m=2000 kg; M=1,4·10²² kg; R= 7000 km.

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EJERCICIO F2BE2824, RESUELTO PASO A PASO. FÍSICA 2º BACHILLERATO. GRAVITACIÓN. EXAMEN EBAU/PAU JULIO 2024 CANARIAS

EJERCICIO F2BE2847, (F2BE2824 AMPLIADO):

Una sonda espacial de masa m es lanzada verticalmente desde la superficie de un planeta de masa M y radio R.

a) Determine la velocidad mínima con la que debe ser lanzada la sonda para que escape del planeta. (Indicar con rigor los razonamientos que nos llevan a la expresión que permite el cálculo)

INTERESA PARA ESTE APARTADO LA CONSULTA DEL CONTENIDO TEÓRICO: VELOCIDAD DE ESCAPE

c) Calcule el peso de la sonda y su aceleración, cuando se encuentra una distancia de 700 km sobre la superficie del planeta.

d) Si a la altura de 700 km se consigue que la sonda se quede en órbita, indicar el tiempo en horas que la sonda describe una vuelta completa al planeta. (Obtener con rigor, a partir de las leyes correspondientes, la expresión que permite el cálculo).

Datos: G = 6,67·10^–11 N m² kg^–2; m=2000 kg; M=1,4·10²² kg; R= 7000 km

IR AL ARTÍCULO CON LA SOLUCIÓN DE ESTE EJERCICIO: EXAMEN RESUELTO DE FÍSICA DE 2º BACHILLERATO: GRAVITACIÓN Y CAMPO ELECTROSTÁTICO. PRIMER TRIMESTRE 2024-25

EJERCICIO F2BE2836: (PLANTEADO EN EL EXAMEN PAU COMO CUESTIÓN)

Calcule la velocidad con la que ha de ser lanzado un cuerpo de masa m para colocarlo en órbita circular alrededor de la Tierra, de radio igual a cuatro veces el radio de la Tierra.

Datos: G = 6,67·10^–11 N m² kg^–2; M_T=5.98·10²⁴ kg; R_T= 6370 km.

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EJERCICIO F2BE2836, RESUELTO PASO A PASO. FÍSICA 2º BACHILLERATO. GRAVITATORIO. EXAMEN EBAU/PAU JULIO 2024 CANARIAS

EJERCICIO F2BE2634:

Recientemente, se ha descubierto un nuevo planeta con características ligeramente similares a la Tierra en masa y tamaño. Se le ha denominado “Tacande” por su color grisáceo-negruzco, en consideración a los aborígenes de la Palma, una de las Islas Canarias. Para los awaras, tacande significa “tierra quemada”.

Un satélite en órbita a una altura de 4000 km sobre la superficie de Tacande se mantiene en órbita gracias a que lleva una velocidad de 11520 km/h.

a.- Hallar la masa de Tacande.

b.- Hallar el periodo de revolución del satélite; indicarlo en horas y minutos.

c.- Hallar la energía que debemos comunicar al satélite para conseguir que siga en órbita a una altura sobre el planeta de 4250 km.

d.- Hallar la gravedad en la superficie del planeta y la aceleración en la primera órbita.

DATOS: G = 6.67×10^-11 Nm²kg^-2.; R_TACANDE= 5700 km; m_SATÉLITE= 400 kg

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE GRAVITACIÓN EN EL UNIVERSO

EJERCICIO F1BE2671:

Un Astronauta en el planeta Mencey, que será próximamente colonizado, deja caer desde lo alto de su nave de 58 m de alto, “amenceyada” (aterrizada si fuera en la Tierra) en su superficie, un martillo de 2,5 kg de masa, que impacta contra el suelo con una velocidad de 90 km/h, según indica el detector de velocidades de la base de la nave.

Una sonda espacial, enviada meses antes de la llegada de este astronauta indicó que el planeta Mencey tiene un diámetro de 4230 km.

Con los datos que se suministran y teniendo en cuenta que la Constante de Gravitación Universal tiene un valor de 6,67·10^-11 en unidades del S.I., responder a las siguientes cuestiones:

a.- Hallar el tiempo que tarda el martillo en llegar al suelo.

b.- Hallar el valor de la gravedad en la superficie del planeta.

c.- Hallar la masa del planeta Mencey.

d.- Obtener las unidades en el Sistema Internacional de la Constante de Gravitación Universal, partiendo de la Ley de Gravitación Universal.

e.- Hallar el valor de la velocidad de un satélite que orbitando alrededor de Mencey tarda 15 horas en completar una vuelta.

ALTERNATIVA DE CONTINUACIÓN PARA ESTE APARTADO EXCLUSIVAMENTE: Si no has sido capaz de obtener la masa del planeta en los apartados anteriores, utilizar el valor de M_MENCEY = 4,5·10²⁴ kg, (indicarlo claramente en ese caso).

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO

EJERCICIO F1BE2672:

Un senderista en el planeta Guayre, recientemente colonizado y curiosamente con una masa similar a la de la Tierra, observa que como consecuencia de un guayrremoto (terremoto si ocurriera en la Tierra) una roca de 250 kg llega al suelo desde el borde de un risco a una altura de 80 metros, con una velocidad de 120 km/h.

Con los datos que se suministran y teniendo en cuenta que el valor de la Constante de Gravitación Universal tiene un valor de 6,67·10^-11 en unidades del S.I., responder a las siguientes cuestiones:

a.- Hallar el tiempo que tarda la roca en llegar al suelo.

b.- Hallar la aceleración de la gravedad en la superficie de Guayre.

c.- Hallar el radio del planeta Guayre.

d.- Explicar razonadamente y con todo lujo de detalles, al amparo de los resultados obtenidos, cuál de los dos planetas, Tierra o Guayre, tiene mayor densidad.

ALTERNATIVA DE CONTINUACIÓN: Caso que no hayas sido capaz de obtener el Radio con la realidad de los apartados anteriores, utilizar exclusivamente en este apartado y el siguiente el dato R_GUAYRE = 8000 km (indicarlo claramente en ese caso).

e.- Hallar el tiempo que tarda en dar una vuelta completa un satélite que orbita alrededor de Guayre a una altura de 790 km. Indicarlo en ____horas, ____ minutos,____segundos.

DATOS: M_GUAYRE = 5,8·10²⁴ kg; g_TIERRA = 9,8 N/kg; R_TIERRA = 6370 km

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE GRAVITACIÓN

EJERCICIO F2BE2453:

Un satélite de 150 kg de masa orbita circularmente en torno a un planeta cuya masa es de 10²⁴ kg y radio 2000 km. Si la altura de la órbita es de 2 ·10⁴ km, calcule:

a) La aceleración del satélite en su órbita.

b) La energía cinética del satélite.

c) La aceleración de la gravedad que el planeta ejerce en cualquier punto de la órbita que describe el satélite.

DATOS: G = 6,67 · 10⁻¹¹ N · m² · kg⁻²

IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: PRUEBA DE EXAMEN FÍSICA 2º BACHILLERATO. GRAVITATORIO, ELÉCTRICO, MAGNÉTICO, ONDAS

JERCICIO F2BE2454:

La Estación Espacial Tiangong-2 (Palacio Celestial) tiene una masa de 20000 kg. Si se pone en órbita a 400 km sobre el ecuador de la Tierra, calcule:

a) La velocidad y la aceleración orbital de la estación.

b) El número de vueltas que da la estación alrededor de la Tierra en 24 horas.

c) La energía necesaria para trasladar la estación desde la órbita de 400 km a una órbita geoestacionaria.

INTERESA: GRAVITACIÓN EN EL UNIVERSO

DATOS: G = 6,67·10^–11 N m² kg^–2; R_T = 6370 km; M_T = 5,97·10²⁴ kg.

IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: PRUEBA DE EXAMEN FÍSICA 2º BACHILLERATO. GRAVITATORIO, ELÉCTRICO, MAGNÉTICO, ONDAS

EJERCICIO F2BE2304:

En el año 2065 un meteorito de elevadas dimensiones se acerca a la Tierra, pero en ese momento disponemos de una tecnología super avanzada que nos permite con un rayo de plasma hipersónico orientado convenientemente, modificar la velocidad de los objetos que se acercan a la Tierra.

El dispositivo sólo permite actuar en objetos astronómicos que se encuentran como máximo a la mitad de la distancia entre la Tierra y la Luna.

Indicar a los operarios del rayo de plasma hipersónico la velocidad que le deben comunicar al meteorito para que en vez de chocar contra la Tierra, se quede enganchado en una órbita justo en la zona más alejada, donde el rayo es efectivo.

DATOS: Utilizar el método BLV para encontrar en internet los datos que sean necesarios.

EJERCICIO FQ1BE2678:

Para un planeta aislado, recientemente descubierto, de masa M_P=3,9·10²⁴ kg y de 6000 km de radio, responder a las siguientes cuestiones de interés:

a.- Hallar el valor de la gravedad en la superficie del planeta.

b.- Hallar el tiempo que tarda en dar una vuelta completa un satélite que orbita alrededor del planeta a una altura de 23000 km sobre su superficie.

c.- Hallar la velocidad del satélite en su órbita.

d.- Hallar la aceleración del satélite en su órbita.

e.- Dejamos caer un martillo de 4 kg desde una altura de 20 metros sobre la superficie del planeta. Hallar la velocidad con la que llega al suelo y compararla haciendo los comentarios apropiados con la que llegaría al suelo si la misma experiencia se realizara sobre la superficie de la Tierra.

DATOS: G=6,67·10^-11 u.S.I.; g_{SUPERFICIE TERRESTRE} = 9,8 m/s²

IR A LA SOLUCIÓN DEL EJERCICIO

EJERCICIO F2BE2356, EBAU CANARIAS JUNIO 2022, ligeramente modificado y ampliado:

Un satélite de 2000 kg de masa se encuentra a una altura de 36000 km, por encima del ecuador, describiendo una órbita circular geoestacionaria. Responder a las siguientes cuestiones:

La velocidad del satélite en su órbita, obteniendo la expresión que la calcula haciendo los razonamientos apropiados con rigor.
Comprobar que efectivamente a la altura indicada aproximadamente, es donde podemos colocar un satélite geoestacionario.
La energía del satélite en su órbita, argumentando convenientemente.
La aceleración y el peso del satélite en su órbita.
Después de un tiempo de funcionamiento, el satélite pierde energía y se mueve en una nueva órbita circular, con una energía total de – 9,526·10⁹ ¿Con qué velocidad lo hace?

Datos: G = 6,67·10⁻¹¹ N·m² ·kg⁻² ; R_T = 6370 km; M_T = 5,98·10²⁴ kg

EJERCICIO F2BE2357, EBAU CANARIAS JUNIO 2022,

Determinar el valor de la intensidad del campo gravitatorio creado por la Tierra en un punto de su superficie. ¿A qué distancia del centro de la Tierra el valor de dicha intensidad se reducirá un cuarto de su valor en la superficie?

Datos: G = 6,67·10⁻¹¹ N·m² ·kg⁻² ; R_T = 6370 km; M_T = 5,98·10²⁴ kg

EJERCICIO F2BE2362, MODIFICADO DE EBAU CANARIAS JUNIO 2022,

Datos: G = 6,67·10⁻¹¹ N·m² ·kg⁻² ; R_T = 6370 km; M_T = 5,98·10²⁴ kg

EJERCICIO F2BE2358, EBAU CANARIAS JULIO 2022, ligeramente ampliado:

En la superficie de un planeta de 3000 km de radio la aceleración de la gravedad es de 6 ms^-2 . A una altura de 5·10⁴ km sobre la superficie del planeta se mueve, en una órbita circular, un satélite de masa 200 kg. Calcular:

La masa del planeta.
La velocidad y aceleración del satélite en la órbita.
La energía potencial y total del satélite en dicha órbita, haciendo comentarios a la diferencia que existe entre ambas, no sólo cualitativas sino cuantitativas.
El valor del campo gravitatorio en la superficie del planeta.
El valor de la fuerza gravitatoria que experimentará un cuerpo de 1 kg de masa colocado en la superficie del planeta.

Datos: G = 6,67·10⁻¹¹ N·m² ·kg⁻²

EJERCICIO F2BE2371:

Se desea colocar un satélite de telecomunicaciones, con una masa de 200 en una órbita que se encuentre a 48 km de altura.

a.- Hallar la energía que tendrá el satélite en esa órbita.

b.- Hallar la velocidad que hay que comunicarle desde la superficie de la Tierra para que alcance esa órbita.

DATOS: g₀=9,8 m/s²; R_T=6,4·10⁶ m

SOLUCIONES: -6,3·10⁹ J; 7949 m/s

EJERCICIO F2BE2372:

Un satélite de 600 kg se encuentra orbitando a una altura de 1200 km sobre la superficie terrestre. Hallar la energía que hay que suministrar al satélite para que escape de la acción del campo gravitatorio terrestre desde esa órbita, con la intención que no se siga acumulando basura espacial.

Datos: G = 6,67·10⁻¹¹ N·m² ·kg⁻²; R_T = 6370 km; M_T = 5,98·10²⁴ kg

SOLUCIÓN: 1,71·10¹⁰ J

EJERCICIO F2BE2373:

Pretendemos que un satélite de 50 kg de masa se mantenga en órbita alrededor de la tierra a una altura equivalente al radio de la Tierra. Hallar:

a.- La energía que se debe comunicar al satélite para que alcance esa órbita, haciendo las suposiciones apropiadas.

b.- La energía que hay que comunicarle para que desde esa órbita, escape del campo gravitatorio terrestre.

Datos: G = 6,67·10⁻¹¹ N·m² ·kg⁻²; R_T = 6370 km; M_T = 5,98·10²⁴ kg

EJERCICIO F2BE2374:

Un satélite artificial de 500 kg de masa se encuentra en órbita circular alrededor de la Tierra a 300 km de su superficie. Hallar:

a.- El valor de la velocidad que lleva el satélite.

b.- El tiempo que tarda en realizar una órbita completa.

c.- La aceleración que posee el satélite.

d.- El campo gravitatorio a esa altura sobre la superficie terrestre.

e.- La energía mecánica del satélite.

f.- La energía que se tuvo que comunicar desde la superficie para conseguir ponerlo en esa órbita, o lo que es lo mismo, el trabajo que se necesita para poner el satélite en esa órbita.

SOLUCIONES: 7744 m/s; 1,5 horas; 9 m/s²; 9 m/s²; -1,5·10¹⁰ J: 1,64·10¹⁰ J:

EJERCICIO F2BE2391:

La Estación Espacial Internacional, con una masa de 420 toneladas gira a una altura media de 419 km sobre la superficie de la Tierra, en una órbita circular. Debido al rozamiento con la alta atmósfera, su altura disminuye continuamente. Por este motivo ha descendido hasta una altura de 400 km.

a.- Obtener la expresión de la velocidad orbital, razonando con rigor.

b.- Obtener la tercera Ley de Kepler, razonando con rigor.

c.- Hallar la velocidad orbital de la estación a 400 km de altura.

d.- La energía necesaria para que recupere la órbita inicial, indicando si hay que comunicársela o debe perderla.

e.- Hallar el peso de la estación en la órbita de 400 km e indicar y justificar el porcentaje de aumento o disminución con respecto al peso en la superficie de la Tierra.

f.- Hallar el periodo en horas de la estación en la órbita de 400 km, así como indicar el número de vueltas que realiza a la Tierra en un día.

DATOS: G=6.67·10^-11 U.S.I.; M_T=5.98·10²⁴ kg; R_T=6370 km

SOLUCIONES: 7675,72 m/s; 10E11 J; 3.66E6 N; 1,54 horas, 15 vueltas y media

EJERCICIO FQ1BE2402:

La nave Bentaiga II, cuando se encuentra a 30 metros de la superficie de Marte, deja caer un paquete de suministros, que se observa que impacta con la superficie de Marte a una velocidad de 15 m/s.

Teniendo en cuenta que el radio de Marte es de 3390 km, y que durante esos 30 metros de caída libre, además de considerar constante la gravedad, se desprecia el rozamiento con la atmósfera tan ligera de Marte, hallar:

a.- El valor de la aceleración de la gravedad en la superficie de Marte.

b.- La masa del planeta.

DATO: G=6.67·10^-11 Nm²kg^-2

VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/2cbpTFkmJ6k

EJERCICIO F2BE2423:

Marte tiene dos satélites: Deimos y Fobos. Fobos es un pequeño satélite de forma irregular, que podemos considerar con un diámetro de 22 km. Orbita a unos 6000 km de la superficie de Marte y tiene una velocidad orbital de 7697 km/h.

a.- Hallar la masa de Marte y la gravedad en su superficie.

b.- La aceleración de Fobos (obtenerla de dos modos diferentes y contrastar los resultados)

c.- El periodo de traslación de Fobos en días terrestres, expresado en forma decimal y en términos de fracción.

d.- Obtener con la expresión adecuada las unidades de la constante de gravitación universal en el sistema internacional de unidades.

DATOS: R_MARTE=3389,5 km; G=6,67·10^-11 u.S.I.

IR AL ARTÍCULO QUE TIENE SOLUCIÓN DEL EJERCICIO: PRUEBA DE EXAMEN DE FÍSICA DE 2º DE BACHILLERATO

EJERCICIO F2BE2442:

Con los datos suministrados, determinar el valor de la intensidad del campo gravitatorio creado por la Tierra en un punto de su superficie. ¿A qué distancia de la superficie de la Tierra el valor de dicha intensidad se reducirá un tercio de su valor en la superficie?

Datos: G = 6,67·10⁻¹¹ N·m² ·kg⁻² ; R_T = 6370 km; M_T = 5,98·10²⁴ kg

IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: PRUEBA DE EXAMEN DE FÍSICA DE 2º BACHILLERATO (X883)

EJERCICIO FQ1BE2482:

Un pequeño satélite artificial de 300 kg de masa, se pretende utilizarlo en la detección de incendios en Tamadaba, con lo que tiene que ser un satélite geoestacionario, colocado encima de Gran Canaria todo el tiempo. Para ello tiene que tener un periodo de revolución en la órbita de 24 horas igual que el periodo de rotación de la Tierra.

a.- Obtener con todo lujo de detalles la 3ª Ley de Kepler.

b.- Dibujar la situación indicando TODAS las fuerzas que actúan sobre el satélite.

c.- La altura sobre la superficie de la Tierra a la que se encuentra el satélite.

d.- El radio de la órbita del satélite.

e.- La velocidad del satélite en su órbita.

f.- La aceleración del satélite en su órbita.

g.- La fuerza gravitatoria que sufre el satélite cuando se encuentra en la superficie de la Tierra antes de que despegue el cohete que lo va a trasladar a su órbita geoestacionaria.

h.- Por causa de una tormenta solar el satélite modifica su posición quedándose en una órbita que se encuentra situada a 40 000 km de altura sobre la superficie de la Tierra. En este caso, hallar la velocidad que debe tener para mantenerse en esa órbita.

i.- Hallar el periodo en esa nueva órbita a 40 000 km de altura

j.- Hallar la aceleración del satélite en esa nueva órbita a 40 000 km de altura.

DATOS: G=6.67×10^-11 Nm²kg-².; R_T=6370 km; M_T=5.98×10²⁴ kg.

IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE GRAVITACIÓN EN EL UNIVERSO PARA FÍSICA DE BACHILLERATO. LEYES DE KEPLER

CUESTIÓN F2BE2465:

¿Qué se entiende por velocidad de escape? Como aplicación, obtenga la velocidad de escape de la Luna.

IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO Y OTROS DE INTERÉS PARA FÍSICA DE 2º DE BACHILLERATO: PRUEBA DE EXAMEN FÍSICA 2º BACHILLERATO. GRAVITATORIO, ELÉCTRICO, MAGNÉTICO, ONDAS

EJERCICIO F2BE2492:

Venus es el segundo planeta en proximidad al Sol. Posee el día más largo del sistema solar (243 días terrestres es su periodo de rotación).

a.- Con los datos suministrados hallar la altura sobre la superficie de Venus a la que habría que colocar un satélite estacionario (que esté siempre encima del mismo punto del planeta, en su ecuador).

b.- La órbita de Venus alrededor del Sol es la más parecida a una circunferencia de todas las del Sistema Solar. Teniendo en cuenta lo anterior y sabiendo que la distancia de Venus al Sol es de 0,72 u.a. (unidades astronómicas), hallar el periodo del movimiento de traslación de Venus.

c.- ¿Qué es una unidad astronómica? (sin puntuación)

DATOS: G=6.67·10^-11 Nm²/kg²; M_VENUS=4.869·10²⁴ kg; R_VENUS=6051,8 km; M_SOL=1.989·10³⁰ kg; 1u.a.=150·10⁶ km; M_TIERRA=5,972·10²⁴ kg

IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN RESUELTO FÍSICA 2º BACHILLERATO. ONDAS, GRAVITACIÓN Y FÍSICA MODERNA

EJERCICIO F2BE2626:

En el planeta Arretranco-2, recientemente descubierto se desea colocar un satélite, el Sopladera-23, al objeto de estudiar las tormentas de arena que se producen en su superficie, en un punto concreto del planeta.

Los estudios relativos a su movimiento indican que el periodo de rotación del planeta es de 1,4 días terrestres.

Se pide:

a.- Altura a la que debe colocarse el satélite sobre el planeta si se desea que sea estacionario, es decir, esté siempre encima del mismo punto del planeta.

b.- El valor del campo gravitatorio en la superficie del planeta explicando su valor comparandolo con lo que sabemos de la Tierra.

c.- El valor de la aceleración que experimentará un cuerpo en caída libre en las proximidades de la superficie del planeta, despreciando los rozamientos con su atmósfera, que está en estudio.

d.- Velocidad que tiene que tener el satélite.

e.- Energía mecánica del satélite en su órbita.

DATOS: G=6.67×10^-11 Nm²kg^-2.; R_ARRETRANCO=6000 km; M_ARRETRANCO=6×10²⁴ kg; m_SOPLADERA= 400 kg; M_TIERRA=5,98·10²⁴ kg; R_TIERRA=6370 km;

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN INICIAL PARA FÍSICA DE 2º DE BACHILLERATO: CAMPO GRAVITATORIO Y GRAVITACIÓN EN EL UNIVERSO. EJERCICIOS RESUELTOS

EJERCICIO FQ1BE2659:

Dos masas m y m’ están separadas una distancia R. Si las aproximamos hasta una distancia de la décima parte de R, el módulo de la fuerza gravitatoria que actúa entre ellas:

a) Dismimuye 100 veces.

b) Dismimuye 10 veces.

c) Aumenta 10 veces.

d) Aumenta 100 veces.

e) Ni aumenta ni disminuye.

f) Ninguna respuesta de las anteriores es correcta.

Elegir la respuesta correcta, trabajando con todo el rigor posible y razonando profundamente el resultado, acompañando de las Leyes que justifiquen el resultado.

IR A LA RESOLUCIÓN DETALLADA DE ESTE EJERCICIO / CUESTIÓN: EJERCICIO RESUELTO / CUESTIÓN DE RAZONAMIENTO CON LA LEY DE GRAVITACIÓN UNIVERSAL PARA FÍSICA DE BACHILLERATO

EJERCICIO FQ1BE2704:

a.- Hallar la altura a la que hay que colocar un satélite si queremos que tarde dos días en dar una vuelta completa a la Tierra.

b.- Hallar la aceleración del satélite en su órbita. Realizarlo de dos modos diferentes.

c.- Hallar la velocidad del satélite en su órbita. Realizarlo de dos modos diferentes.

6,07E7 m; 0,089 m/s²; 2438,68 m/s

DATOS: G=6.67×10^-11 Nm²kg^-2.; M_TIERRA=5,98·10²⁴ kg; R_TIERRA=6370 km;

EJERCICIO F2BE2873:

Un satélite artificial de 650 kg de masa, destinado al estudio de las tormentas de arena, describe una órbita circular sobre el planeta Snape, recientemente descubierto, a una altura de 250 km. El periodo del satélite es de 3 horas. Con los datos que se suministran, hallar, obteniendo las fórmulas utilizadas que se pueda:

a.- El campo gravitatorio en la superficie de Snape.

b.- La masa de Snape.

c.- La velocidad del satélite.

d.- La energía del satélite en su órbita.

DATOS: G=6.67×10^-11 Nm²kg^-2 ; R_SNAPE=5750 km;

IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE GRAVITACIÓN EN EL UNIVERSO: EXAMEN RESUELTO CON EJERCICIOS DE CAMPOS GRAVITATORIO, ELECTROSTÁTICO Y MAGNÉTICO, CORRESPONDIENTE A PRUEBA FINAL PRIMER TRIMESTRE 2024-25, PARA FÍSICA DE 2º DE BACHILLERATO

EJERCICIO F2BE2979:

Hallar la altura a la que se encuentra un satélite que tarda 20 horas en dar una vuelta completa a la Tierra, obteniendo la expresión que permite su cálculo y nombrándola.

Datos: G = 6,67·10^–11 N·m² ·kg^-2 ; M_T = 5,98·10²⁴ kg; R_T = 6370 km;

IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN RESUELTO DE FÍSICA 2º BACHILLERATO: ONDAS, EFECTO DOPPLER, ELECTROMAGNETISMO Y GRAVITACIÓN. CURSO 2024-25.

PUEDE RESULTAR INTERESANTE LA CONSULTA DE LOS SIGUIENTES ENLACES RELACIONADOS:

PODRÍA INTERESAR LA VISITA AL SIGUIENTE ARTÍCULO DEL PROYECTO, DONDE SE DESARROLLAN LAS ASIGNATURAS DE FÍSICA Y QUÍMICA DE SECUNDARIA Y BACHILLERATO: