ARITMÉTICA Y ÁLGEBRA 1º BACHILLERATO. ECUACIONES CON LOGARITMOS

ARITMÉTICA ÁLGEBRA ECUACIONES LOGARITMOS

Autor: D. José Rodríguez de la Serna

Colaborador al 50% en el proyecto

ECUACIONES CON LOGARITMOS, ¿PARA QUÉ QUIERO YO ESO?:

En esta situación de aprendizaje, trabajaremos la ecuaciones exponenciales y logarítmicas y trataremos de hacer ver su aplicación a otras ciencias o al mundo de las ciencias sociales o incluso humanísticas.

ACTIVIDAD RELACIONADA CON ESTAS OTRAS ACTIVIDADES DEL PROYECTO:

ASPECTOS FORMALES:

CON RESPECTO A LAS COMPETENCIAS CLAVE Y DESCRIPTORES OPERATIVOS ASOCIADOS:

- COMPETENCIA MATEMÁTICA Y EN CIENCIA, TECNOLOGÍA E INGENIERÍA (STEM), concretamente los DESCRIPTORES OPERATIVOS STEM1 , STEM2 , STEM3
  - Sobre todo hacer uso del álgebra para aplicarlas a situaciones del mundo real
- COMPETENCIA EN CONCIENCIA Y EXPRESIÓN CULTURALES (CCEC), concretamente el DESCRIPTOR OPERATIVO CCEC2 y EL DESCRIPTOR OPERATIVO CCEC4.2
  - Uso de soportes diversos y rigor en la presentación de las tareas.
- COMPETENCIA EN COMUNICACIÓN LINGÜÍSTICA (CLL), concretamente los DESCRIPTORES OPERATIVOS CCL1. CCL2
  - Se pedirá un análisis y justificación del razonamiento seguido para el desarrollo de los problemas planteados y se pedirá se dé una respuesta contextualizada
- COMPETENCIA DIGITAL (CD), concretamente el DESCRIPTOR OPERATIVO CD1 , CD2 , CD3 , CD5
  - Búsqueda de información y presentación en formatos digitales
- COMPETENCIA EMPRENDEDORA (CE), concretamente el DESCRIPTOR OPERATIVO CE3
  - Desarrollaremos la elaboración de estrategias para resolver los problemas planteados.
- COMPETENCIA PERSONAL, SOCIAL Y DE APRENDER A APRENDER (CPSAA), concretamente los DESCRIPTORES OPERATIVOS CPSAA4 y CPSAA5
  - Haremos uso del trabajo cooperativo para el desarrollo de esta situación de aprendizaje.

CON RESPECTO A LOS SABERES BÁSICOS DE MATEMÁTICAS DE 1º BACHILLERATO PREDOMINANTES EN LA ACTIVIDAD:

- - I. Sentido Numérico
  - IV. Sentido algebraico
  - VI. Sentido socioafectivo

CON RESPECTO A LAS COMPETENCIAS ESPECÍFICAS DE MATEMÁTICAS DE 1º DE BACHILLERATO QUE SE CONSIDERAN:

MAT BAC C1 , MAT BAC C2 , MAT BAC C3 , MAT BAC C4 , MAT BAC C5 , MAT BAC C6 , MAT BAC C7 , MAT BAC C8 , MAT BAC C9

CON RESPECTO A LOS CRITERIOS DE EVALUACIÓN DE MATEMÁTICAS I DE 1º DE BACHILLERATO QUE SE TRABAJAN:

MATI1BAC1.1 , MATI1BAC1.2 , MATI1BAC2.1 , MATI1BAC4.1 , MATI1BAC5.2 , MATI1BAC6.1 , MATI1BAC7.1 , MATI1BAC8.1 , MATI1BAC8.2

HIPERVINCULADOS A LOS DESCRIPTORES OPERATIVOS DE LAS COMPETENCIAS CLAVE

ESTE MATERIAL TIENE RELACIÓN CON ASPECTOS DEL PERFIL DE SALIDA DEL ALUMNADO DE LOS INSTITUTOS DIOCESANOS DE CANARIAS

TAREAS:

1.- Repaso Inicial: Recordar en clase el concepto de logaritmo y sus propiedades. Se debe para ello consultar las unidades que se aportan como presentación preliminar al final del artículo. Con la finalidad de ver si han quedado claras esas ideas, formaremos grupos de cuatro alumnos y pasaremos el puzzle de los logaritmos, del Anexo II. Una vez montado deben tomar una foto y mandar por TEAMS a la tarea previamente creada.

2.- Hoja de problemas contextualizados: Se reparte una hoja con cuatro problemas a cada grupo. Mediante la técnica de lápices desarrollan los cuatro problemas propuestos. En ellos se plantean ecuaciones exponenciales en diferentes contextos y para cuya resolución tendrán que hacer uso de los logaritmos

3.- Uso de Geogebra para el cálculo de las ecuaciones sugeridas. Para evidenciar el uso del programa se realiza un pantallazo.

4.- Realización Informe: Se debe entregar un dossier con los problemas resueltos, en él deben quedar claras, cuáles son las variables y como se definen. Cuáles son las ecuaciones planteadas partiendo del texto. Cuales han sido los pasos de la resolución del problema. Cuál es la solución expresada mediante una frase que responda al texto de la pregunta. Comprobar que la solución es coherente con el planteamiento inicial.

RÚBRICA DE EVALUACIÓN:

CRITERIO	TAREA	INS	SUF	NOT	SOB
*MATI1BAC1.1* *MATI1BAC1.2* *MATI1BAC2.1* *MATI1BAC4.1* *MATI1BAC5.2* *MATI1BAC6.1* *MATI1BAC7.1* *MATI1BAC8.1* *MATI1BAC8.2*	PROBLEMAS	El planteamiento es inadecuado y/o incompleto en más de dos casos.	El planteamiento es inadecuado y/o incompleto en dos casos.	El planteamiento es inadecuado y/o incompleto en un caso	No existen errores ni en el planteamiento ni en el desarrollo
	INFORME	No se indican las variables en más de dos casos. No se explica la resolución en más de dos casos. La solución no se explica con una frase coherente en más de dos casos. La solución no es coherente con el texto en más de dos casos.	No se indican las variables en dos casos No se explica la resolución dos casos La solución no se explica con una frase coherente en dos casos La solución no es coherente con el texto en dos casos	No se indican las variables en un caso No se explica la resolución un caso La solución no se explica con una frase coherente en un caso La solución no es coherente con el texto en un caso	Se indican todas las variables. Se explican todas las resoluciones. Se explican todas las soluciones con frases coherentes. Todas las soluciones están acorde al contexto
	USO DE LAS TICS	Los resultados no coinciden con geogebra en más de dos casos	Los resultados no coinciden con geogebra en dos casos	Los resultados no coinciden con geogebraen un caso	Los resultados coinciden con geogebra en todos los casos

ANEXO I:

PROBLEMAS:

1. En una muestra de un fósil se detectó que el 0.003% del Carbono contenido es Carbono 14 (¹⁴C).

Si se sabe que el 14C,representa el 1% del Carbono presente en un ser vivo y que la vida media del ¹⁴C es de 5730 años, ¿Qué tan antiguo es el fósil?

DATOS: El decaimiento radiactivo cumple que

Siendo C: Cantidad de isotopo radiactivo; C₀: Cantidad inicial de carbono 14; n: Vida media en años del isotopo; t: Tiempo transcurrido en años.

2.- Sabemos que la cantidad, ‘N’, de insectos en ‘t’ años está dada por una función exponencial del tipo N = N_o · e^kt. Un grupo de biólogos estimó que la población creció en 20% durante los últimos 3 años y saben que si la población crece en un 70% con respecto a la población original se convertiría en una plaga.

¿En cuántos años se estima que la población de insectos se convierta en una plaga?

3.- El crecimiento de la población humana puede describirse mediante una función de crecimiento logístico. Para la población de una isla caribeña se sabe que se ajusta a la función:

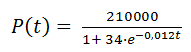
donde t=0 corresponde a la población que había en la isla en el año 2000.

a) ¿Cuántos habitantes habrá en 2025?
b) ¿En cuántos años se duplicará la población con respecto a la que había en 2020?

4.- (EXPEDIENTE M1BE2046)

La temperatura corporal de una persona es de 37º C. Se sabe que cuando una persona fallece, en promedio tarda 20 horas para que su temperatura corporal llegue a 27º C, si la temperatura del medio ambiente permanece a 25º C.

Se supone que el cuerpo humano cumple con la Ley de enfriamiento de Newton, a saber:

T = T’ +C · e^kt

Donde T es la temperatura cuando han pasado «t» horas,

T’ la temperatura del ambiente,

C depende de las condiciones iniciales, ya que se obtiene cuando t=0 (el instante del fallecimiento); de hecho equivale a T – T’.

Un médico forense observa que la temperatura de una persona que falleció es de 29º C y la temperatura ambiente se mantuvo a 25º C desde el fallecimiento.

Si el reloj del médico marca las 7:00 pm, ¿A qué hora se estima el fallecimiento?

ANEXO II:

Puzzle de logaritmos:

https://anagarciaazcarate.files.wordpress.com/2013/10/puzzleblancologaritmosalumnado.pdf

EJERCICIOS ADICIONALES:

EJERCICIO M1BE2043:

Un conjunto de estudiantes han llegado a la conclusión, no sin dificultad, que en un charco en la zona intermareal de la Playa de Las Canteras de Las Palmas de Gran Canaria, si se suministra los suficientes nutrientes y sin que el espacio sea un problema, las bacterias crecen exponencialmente.

El modelo matemático de crecimiento exponencial nos indica que el número de bacterias en función del tiempo: N(t) tiene la siguiente expresión: N(t) = A_o · e^kt , donde Ao es la cantidad inicial, k es la constante de crecimiento y t es el tiempo.

a.- Obtener la expresión que nos indica el número de bacterias en función del tiempo en minutos, sabiendo que inicialmente los estudiantes estiman que habían 500 bacterias en el charco y que diez minutos más tarde el número de bacterias es de 1500.

b.- Utilizar el modelo obtenido para saber, siempre y cuando, ni los nutrientes ni el espacio sean limitados, el número de bacterias que habrá en una hora.

IR AL VÍDEO QUE SOLUCIONA ESTOS DOS PRIMEROS APARTADOS: https://youtu.be/s3orIAQTfPs

c.- Representar la función obtenida en el apartado a mediante geogebra o similar

d.- Reflexionar acerca de la evolución del número de bacterias en el charco, en una situación real, en el sentido de las cuestiones que planteamos a continuación:

d.1.- ¿El comportamiento del crecimiento bacteriano exponencial se mantendrá indefinidamente?

d.2.- Atreverse a representar la evolución del número de bacterias hasta la próxima marea alta.

d.3.- Si no se nos ocurre ninguna idea, recomendamos la consulta del siguiente enlace:

https://es.wikipedia.org/wiki/Crecimiento_bacteriano

e.- Atreverse a enunciar la situación del charco en lo que se refiere al número de bacterias, a través de una función a trozos.

MATERIALES DE INTERÉS:

DE NÚMEROS, ARITMÉTICA,

U1. NÚMEROS REALES

DE ÁLGEBRA,

U2. ÁLGEBRA

Post Views: 1.951