EXAMEN RESUELTO PAU 2025 JUNIO
MATEMÁTICAS II JUNIO ORDINARIA
EXAMEN RESUELTO P.A.U. CANARIAS JUNIO 2025. CONVOCATORIA ORDINARIA:


INTERESA LA CONSULTA DEL SIGUIENTE CONTENIDO RELACIONADO: EXAMEN RESUELTO P.A.U. CANARIAS JULIO 2025 MATEMÁTICAS II. CONVOCATORIA EXTRAORDINARIA
PARA LA PREPARACIÓN DE LA PRUEBA O UNA SIMILAR CONVIENE LA CONSULTA DE LOS SIGUIENTES MATERIALES DE ESTE PROYECTO DE MEJORA DEL APRENDIZAJE EN CIENCIAS:
- FUNCIONES: ANÁLISIS PARA 1º BACHILLERATO
- APLICACIONES DE LA DERIVADA. OPTIMIZACIÓN Y CÁLCULO DE PARÁMETROS.
- GEOMETRÍA ESPACIAL PARA BACHILLERATO
- EJERCICIOS DE CÁLCULO DE PROBABILIDADES PARA MATEMÁTICAS DE 2º BAC
- MATRICES Y DETERMINANTES PARA BACHILLERATO.
- EXÁMENES RESUELTOS PASO A PASO DE MATEMÁTICAS 2º BACHILLERATO
SIGUE EL ESQUEMA PLANTEADO PARA EL SEGUIMIENTO DE LA ASIGNATURA DE MATEMÁTICAS II DE 2º DE BACHILLERATO: MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
LOS ENUNCIADOS DE LA PRUEBA PAU JUNIO 2025 ORDINARIA, PÁGINA 1:
LOS ENUNCIADOS DE LA PRUEBA PAU JUNIO 2025 ORDINARIA, PÁGINA 2:
LOS EJERCICIOS Y SU RESOLUCIÓN PASO A PASO:
EJERCICIO M2BE3220:
En un hospital de las Islas Canarias, un equipo de investigación está analizando cómo se metaboliza en sangre un nuevo medicamento llamado Metabolix, utilizado para tratar infecciones bacterianas. La concentración residual del fármaco en el plasma sanguíneo, denotada como f(x) (medida en miligramos por litro, mg/L), depende del tiempo transcurrido x (en horas) desde su administración. El estudio indica que el medicamento sigue dos fases diferenciadas:
- Fase de absorción: En las primeras dos horas, el fármaco se distribuye por el organismo.
- Fase de eliminación: A partir de la segunda hora, el fármaco empieza a eliminarse.
Este comportamiento se modeliza mediante la siguiente función matemática:
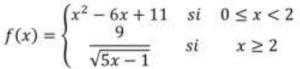
El equipo de investigación necesita aclarar algunas dudas del modelo matemático:
a) Confirmar si este modelo es realmente continuo. Justifica tu respuesta.
b) La concentración residual varía con el tiempo, comprobar que la velocidad de crecimiento instantánea de la concentración residual a las 3 horas de administrar Metabolix es mayor que -0.5 (mg/L)/h.
c) ¿Es cierto que la concentración residual del fármaco en la sangre siempre va disminuyendo con respecto al tiempo transcurrido? Averiguar en qué instante la concentración residual es máxima у calcular el valor de dicha concentración.
d) Pasado un largo periodo de tiempo, ¿cuál será la concentración residual de este medicamento?
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO M2BE3220 RESUELTO, CONTEXTUALIZADO DE ANÁLISIS. PAU CANARIAS JUNIO 2025
EJERCICIO M2BE3221:
Dada la matriz M ∈ M2×2 , con a ∈ ℜ, siendo M, la matriz siguiente:
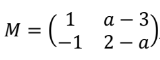
a.- Para cualquier valor del parámetro a: comprobar que M es invertible y dar la expresión de M-1.
b.- Para a = -1 . calcula el valor de la matriz X que satisface la ecuación MA = B – MX, siendo A y B las siguientes matrices:
![]()
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE3221 DE MATRIZ INVERSA Y ECUACIONES MATRICIALES. PAU CANARIAS JUNIO 2025
EJERCICIO M2BE3222:
Dada la matriz A siguiente, con k ∈ ℜ:
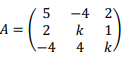
a.- Estudiar el rango de A según los valores del parámetro k.
b.- Para k = -1, comprobar que A2 = 2A – I, donde I denota la matriz identidad de orden 3. Además utilizando la igualdad anterior verifica, sin calcular la potencia, que A4 = 4A – 3I .
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE3222 DE MATRICES Y ECUACIONES MATRICIALES. PAU CANARIAS JUNIO 2025
EJERCICIO M2BE3223:
En el espacio tridimensional, dados el punto P y las rectas r1 y r2 siguientes:
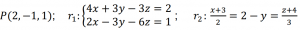
a) Comprobar que P ∈ r1 y que P ∉ r2
b) Hallar la distancia entre el punto P y el punto de intersección de las rectas r1 y r2
c) Hallar el ángulo con el que se cortan las rectas r1 y r2
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO M2BE3223, RESUELTO DE GEOMETRÍA EN EL ESPACIO PARA BACHILLERATO. DISTANCIAS Y ÁNGULOS. PAU CANARIAS JUNIO 2025
EJERCICIO M2BE3224:
En el espacio tridimensional se consideran los siguientes elementos geométricos:
![]()
a) Hallar la posición relativa del plano 𝜋 y la recta 𝑟.
b) Hallar el punto simétrico de 𝐴 con respecto del plano 𝜋.
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO M2BE3224 RESUELTO DE GEOMETRÍA ESPACIAL PARA BACHILLERATO. PAU CANARIAS JUNIO 2025
EJERCICIO M2BE3225:
En una feria, un participante tiene la oportunidad de ganar premios eligiendo entre tres cajas sorpresa: una con premio y dos vacías. Hay una regla especial si se selecciona una caja vacía:
En caso de elegir una caja sin premio, se debe extraer al azar una bola de una urna compuesta por 2 bolas verdes y 3 negras, de idéntica forma y tamaño. Si se elige la bola negra, finaliza la jugada sin premio. Si se elige la bola verde, tendrá la oportunidad de elegir una nueva caja, de las dos cajas no seleccionadas anteriormente, y acabaría la jugada.
Responder a las siguientes cuestiones:
a) Dibujar un diagrama de árbol que refleje todos los posibles casos de este juego.
b) Calcular la probabilidad de obtener premio en este juego.
c) Si el participante ha obtenido premio, ¿ cuál es la probabilidad de que haya elegido una bola verde en la urna?
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE3225, DE PROBABILIDAD DIAGRAMA EN ÁRBOL. PAU CANARIAS JUNIO 2025
EJERCICIO M2BE3226:
La temperatura diurna en el Parque Nacional de las Cañadas del Teide durante el mes de agosto sigue una distribución normal. La temperatura media durante el día es de 22ºC con desviación típica de 5ºC. Además, se sabe que, las condiciones ideales para realizar senderismo es cuando la temperatura diurna se sitúa entre 18ºC y 25ºC. Si se superan los 30ºC, los excursionistas tendrían un riesgo elevado de insolación. Mientras que, si la temperatura se sitúa por debajo de los 15ºC, existe riesgo de cambios meteorológicos bruscos previstos para ese día.
Se está elaborando una guía informativa para los servicios de emergencia. Responder a lo siguiente:
a) ¿Qué probabilidad hay de que un día de agosto se den las condiciones ideales para realizar senderismo?
b) ¿Cuántos días de agosto se espera que haya senderistas con riesgo de insolación?
c) Si las Cañadas del Teide recibe un promedio de 11000 visitantes diarias en el mes de agosto y, de ellos, un 5% realiza senderismo. ¿Cuántos senderistas se estima que se puedan ver afectados por cambios meteorológicos bruscos a lo largo de dicho mes?
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE3226 DE PROBABILIDAD. DISTRIBUCIÓN NORMAL DE PROBABILIDADES. PAU CANARIAS JUNIO 2025
