PÉNDULO SIMPLE MOVIMIENTO ARMÓNICO
PÉNDULO SIMPLE: MOVIMIENTO ARMÓNICO. OBTENCIÓN DE LA GRAVEDAD EN CLASE:

INTERESA LA CONSULTA DEL SIGUIENTE MATERIAL RELACIONADO:
SIGUE EL PROCESO DETERMINADO POR:
- FÍSICA Y QUÍMICA DE 1º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
- FÍSICA DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
PÉNDULO SIMPLE:
Definición: «El péndulo simple o matemático está constituido por un punto material de masa m suspendido de un punto fijo sin rozamiento, por un hilo inextensible (no es elástico ni deformable) y de masa despreciable».
Se le desplaza de su posición de equilibrio un cierto ángulo α con la vertical y se suelta. Todos podemos ver que tiende a recuperar la posición de equilibrio e incluso sigue más allá, describiendo un movimiento de vaivén en torno a la posición de equilibrio. Si no hubiera rozamiento con el aire incluso estaría moviéndose indefinidamente.
Para lo que viene a continuación imaginaremos que no existe el rozamiento con el aire.
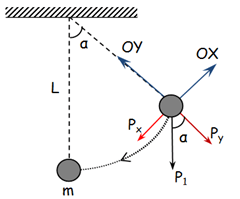
Desplazamos la masa m tal y como decimos un ángulo α con la vertical y lo soltamos.
La dinámica de este movimiento, una vez lo soltamos, en el eje OX y según el sistema de referencia elegido, es decir la aplicación de la LEY FUNDAMENTAL DE LA DINÁMICA, 2º LEY DE NEWTON:
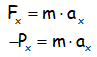
Ya que hemos dicho que no existe rozamiento con el aire, la única fuerza que existe es el peso.
Notar como el signo negativo del Px es debido a que tiene sentido diferente del que hemos considerado positivo para el eje OX, según el sistema de referencia elegido.
Teniendo en cuenta que podemos descomponer el peso en cada uno de los ejes considerados (eje OX y eje OY).
La componente del peso en el eje OY, no nos interesa, ya que en esa dirección no se produce movimiento.
La componente x del peso utilizando la trigonometría y teniendo en cuenta que el peso es igual a la masa por la gravedad g:
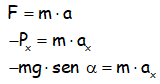
Que además, como podemos simplificar las masas al estar en los dos miembros de la ecuación, nos va quedando:
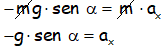
Por lo tanto, la aceleración en el eje OX de este movimiento (que es donde únicamente se produce movimiento) es:
![]()
Al respecto de lo anterior, podemos hacer una serie de APROXIMACIONES:
Una de las consecuencias de la medida del ángulo en radianes es que para ángulos a pequeños, el seno del ángulo a coincide, casi tiene el mismo valor que el propio ángulo a (comprobarlo con calculadora para pequeños ángulos (hasta 15º sexagesimales).
Teniendo esto en cuenta, si suponemos que trasladamos la masa m de su posición de equilibrio un ángulo pequeño, la masa m, comenzará a oscilar con una aceleración:
![]()
Como además sabemos que «un radián es el ángulo que abarca un arco cuya longitud es igual al radio» o lo que es lo mismo, cuando el ángulo α está expresado en radianes:
![]()
Si llamamos al Arco “x” por eso de que es la distancia que hemos desplazado la masa m y tenemos en cuenta que el radio del movimiento es la longitud del péndulo L:
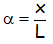
Donde a es el ángulo en radianes, x la longitud del arco, y L la longitud del péndulo.
La aceleración se puede poner teniendo todo lo anterior en cuenta:
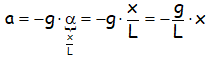
Que es la ecuación que identifica un M.A.S. (MOVIMIENTO ARMÓNICO SIMPLE).
Según esto, para ángulos pequeños, un péndulo simple describe un movimiento armónico simple: esto es, un movimiento de vaivén especial, que entre otras cosas, la aceleración es igual a – w2·x . Siendo w la velocidad angular de un movimiento circular que coincide con 2π/T, siendo T igual al periodo del movimiento armónico simple (tiempo que tarda en completarse el movimiento de vaivén – un recorrido de ida y vuelta completo-) .
Por ello, relacionando las dos ecuaciones para la aceleración, la que acabamos de obtener y la del Movimiento Armónico Simple:
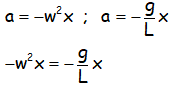
Que está claro que podemos simplificar la x al estar en los dos miembros, así como quitar el signo:
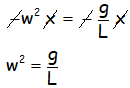
Tomando raíces cuadradas en los dos miembros para quitar el cuadrado de w:
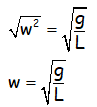
Teniendo en cuenta que w coincide con 2π/T, esto nos posibilita poner lo anterior en función del periodo T, que es más fácil de obtener.

Si queremos despejar el periodo T, nos queda:
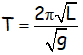
Si por el contrario, quisiéramos despejar la g, la aceleración de la gravedad, tendríamos que elevar previamente al cuadrado:
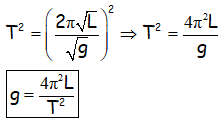
Que es la fórmula que andábamos buscando, la que nos permite obtener el valor de la gravedad en un lugar determinado, con una cuerda y una masa, midiendo el tiempo que tarda en completarse el movimiento de vaivén y la longitud del hilo del péndulo simple.
PUEDE INTERESAR VER UNA PRÁCTICA REAL DE OBTENCIÓN DE LA GRAVEDAD EN CLASE, UTILIZANDO UN PÉNDULO SIMPLE: DETERMINACIÓN DE LA GRAVEDAD EN CLASE
EJERCICIO F2BE3447:
En la Luna, un astronauta quiere confirmar el valor de la gravedad en su superficie, dato que él conoce, con lo que en el taller del módulo lunar, cuando alunizó, preparó un péndulo, con una bolita de 25 g de masa. Si resulta que el péndulo, cuando lo hace oscilar mide un periodo de 3,12 segundos (medido con un super cronómetro).
a.- ¿Cuánto mide el péndulo?.
b.- Si ese mismo péndulo, cuando el astronauta vuelve a la nave que se encuentra orbitando sobre la Luna, resulta que tiene un periodo de 4,5 segundos (suponiendo que la aceleración de la nave no afecta al movimiento del péndulo), ¿a qué altura se encuentra orbitando sobre la Luna?.
c.- Hallar el periodo de la nave en la órbita (en horas), obteniendo y nombrando las fórmulas que se apliquen en la resolución del ejercicio.
Datos: G = 6,67 · 10−11 N m2 kg−2; RL = 1737 km; ML = 7,34 · 1022 kg.
SOLUCIONES: 40 cm, 763 km; 3,12 horas
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: PÉNDULO SIMPLE. EJERCICIO RESUELTO DE OBTENCIÓN DE LA GRAVEDAD EN LA LUNA
EJERCICIO F2BE3452:
Recientemente se ha descubierto un nuevo planeta, de dimensiones similares a la Tierra, al que se le ha denominado Voldemort, por el aspecto desagradable que muestra su exterior. Un astronauta en su superficie, utilizando un péndulo de 50 cm de longitud observa que el mismo tiene un periodo de 1,5 segundos.
Hallar la masa del planeta.
Datos: G = 6,67 · 10−11 N m2 kg−2; RVoldemort = 5900 km
SOLUCIÓN: 4.58·1024 kg
EJERCICIO F2BE3453:
Buscando en la red, hemos visto que el valor de la gravedad en la superficie de la Tierra, no es una constante, encontrando valores significativos en los Polos, en el Ecuador y en la cima del Everest, que ponemos a continuación:
g Polos = 9,832 m/s2
g Ecuador = 9,781 m/s2
g Everest = 9,773 m/s2
Atreverse a decir el motivo del por qué existe esta diferencia y calcular el periodo de un péndulo simple de 50 cm de largo, aproximando al ms, en cada uno de los casos.
