TEOREMA ROUCHÉ FRÖBENIUS DISCUSIÓN
TEOREMA DE ROUCHÉ-FRÖBENIUS, PARA DISCUSIÓN DE SISTEMAS DE ECUACIONES LINEALES:
PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
SIGUE EL ESQUEMA PLANTEADO PARA EL SEGUIMIENTO DE LA ASIGNATURA DE MATEMÁTICAS II DE 2º DE BACHILLERATO: MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
TEOREMA DE ROUCHÉ:
«LA CONDICIÓN NECESARIA Y SUFICIENTE PARA QUE UN SISTEMA LINEAL TENGA SOLUCIONES, ES QUE EL RANGO DE LA MATRIZ DE LOS COEFICIENTES DE LAS INCÓGNITAS (A), COINCIDA CON EL RANGO DE LA MATRIZ AMPLIADA (A*)»
Cuando un sistema tiene solución, decimos que es COMPATIBLE, del mismo modo, cuando no tiene solución decimos que es INCOMPATIBLE. Por ello, para que un sistema sea compatible los rangos de la matriz de los coeficientes y de la ampliada tienen que coincidir.
Entendemos que el sistema se encuentra colocado del siguiente modo:
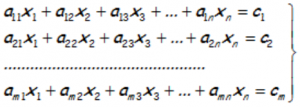
Donde la matriz de los coeficientes (A) y la matriz ampliada (A*) se corresponden con las siguientes:
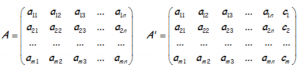
PUEDE INTERESAR IR A LA DEMOSTRACIÓN DEL TEOREMA DE ROUCHÉ, EN EL SIGUIENTE ARTÍCULO: TEOREMA DE ROUCHE
TEOREMA DE ROUCHÉ-FRÖBENIUS:
Se entiende generalmente que supone una ampliación del Teorema de Rouché, o una concreción del mismo, atendiendo al número de soluciones del sistema de ecuaciones.
Si además de la coincidencia de rangos entre las matrices de los coeficientes y la ampliada, el rango es igual al número de incógnitas, el sistema sería COMPATIBLE DETERMINADO (tendría una única solución).
Si el valor de la coincidencia de rangos es inferior al número de incógnitas, el sistema sería COMPATIBLE INDETERMINADO (tendría infinitas soluciones).
En este último caso, la diferencia entre el valor del número de incógnitas y el valor de la coincidencia de rangos nos daría el número de GRADOS DE LIBERTAD de las soluciones del sistema indeterminado (que no es sino el número de parámetros en función de los cuales aparecen las soluciones λ, μ…)
IR A EJERCICIOS DE APLICACIÓN DE ESTE TEOREMA: DISCUSIÓN Y RESOLUCIÓN DE SISTEMAS LINEALES. ROUCHÉ Y CRAMER. EJERCICIOS RESUELTOS


