EJERCICIO APLICACIÓN PROPIEDADES LOGARITMOS
EJERCICIO RESUELTO M1BE0339 DE APLICACIÓN DE LAS PROPIEDADES DE LOS LOGARITMOS. ARITMÉTICA PARA BACHILLERATO:

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- EJERCICIOS DE APLICACIÓN DE LAS PROPIEDADES DE LOS LOGARITMOS. ARITMÉTICA PARA BACHILLERATO
- ARITMÉTICA PARA SECUNDARIA Y 1º DE BACHILLERATO
- UTILIDAD DE LOS LOGARITMOS. LEYES DE KEPLER
- ECUACIONES LOGARÍTMICAS PARA MATEMÁTICAS DE SECUNDARIA Y BACHILLERATO
- SISTEMAS DE ECUACIONES LOGARÍTMICAS
ESTE MATERIAL SIGUE EL PROCESO DETERMINADO POR:
- MATEMÁTICAS I DE 1º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
- MATEMÁTICAS DE 4º DE LA E.S.O.. DESARROLLO DE LA ASIGNATURA
RESUMEN DE LOGARITMOS:
DEFINICIÓN DE LA OPERACIÓN LOGARITMO:
![]()
CONSECUENCIAS DE LA DEFINICIÓN DE LOGARITMO:
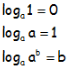
PROPIEDADES DE LOS LOGARITMOS:
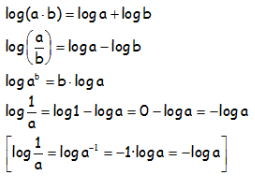
EJERCICIO M1BP0339:
Sabiendo que log 2 = 0,3010 y log 3 = 0,4771, calcular con una calculadora de parvulitos (sin tecla log):
a.- log 14,4 =
b.- log (1,6 · 0,32) =
c.- log 5,12 =
d.- log 16,2 =
e.- log 0,3 =
f.- log 0,02 =
RESOLUCIÓN DE ESTE EJERCICIO:
