MATRIZ INVERSA MATEMÁTICAS BACHILLERATO
MATRIZ INVERSA, PARA MATEMÁTICAS DE BACHILLERATO:
PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
SIGUE EL ESQUEMA PLANTEADO PARA EL SEGUIMIENTO DE LA ASIGNATURA DE MATEMÁTICAS II DE 2º DE BACHILLERATO: MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
La matriz inversa es la que al multiplicarla con la matriz de la que es inversa, nos devuelve el elemento neutro del producto:
![]()
Si bien la propiedad conmutativa no siempre se cumple en el producto de matrices, sí se cumple en este caso.
Donde la matriz I (identidad), el elemento neutro del producto de matrices. En el caso de matrices 3×3:
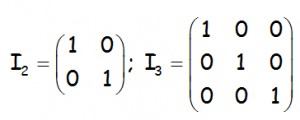
Todos los elementos son nulos, salvo los elementos de la diagonal principal.
Notar como efectivamente, la matriz I, es el elemento neutro del producto de matrices, viendo el siguiente ejemplo de orden 2:
![]()
Si bien la propiedad conmutativa no siempre se cumple en el producto de matrices, sí se cumple en este caso.
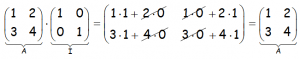
Una matriz cuadrada tiene inversa cuando su determinante es distinto de cero. En este caso se dice que es regular. En este caso, la matriz inversa de A se puede obtener del siguiente modo:
Si A es la matriz:
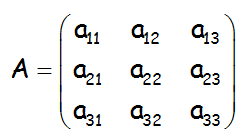
Su inversa será:
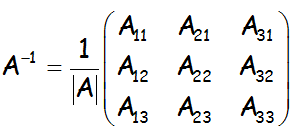
Donde A21, por ejemplo, indica el adjunto del elemento a21.
Debemos notar, por lo tanto, que la matriz con la que obtenemos la inversa es la matriz de los adjuntos pero traspuestos: sus elementos son los adjuntos de cada uno de los elementos pero están traspuestos (cambiadas las filas por las columnas).
Operativamente lo conveniente es:
1.- Obtener el determinante. Si es cero, no tiene inversa.
2.- Elaborar la matriz de los menores complementarios de cada elemento (αij)
3.- Cambiar el signo para obtener la matriz de los adjuntos (Aij)
4.- Trasponer esa matriz para obtener la matriz de los adjuntos traspuesta (Aji)
5.- No olvidar dividir cada elemento por el valor del determinante.
EJERCICIO M2BE1959:
a.- Matriz inversa: Definición.
b.- Hallar la matriz inversa de A, siendo A:
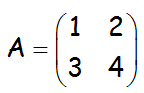
c.- Comprobar que la matriz inversa (A-1) obtenida en el apartado anterior, realmente es la inversa de A, realizando el producto correspondiente.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/_zRORL9wjjs
EJERCICIO M2BE1960:
Hallar la matriz inversa de A, siendo A:
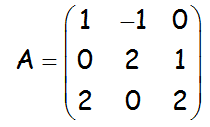
SOLUCIÓN:
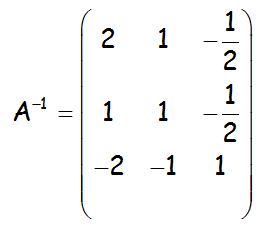
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/zHNKKOOS3vg
EJERCICIO M2BE2039:
Hallar la matriz inversa de cada una de las siguientes matrices:
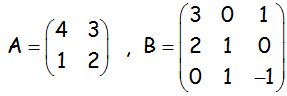
VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/FUFPefZRuxM
EJERCICIO M2BE1997 JL:
Siendo A y B las siguientes matrices:
![]()
¿Cuándo AB tiene inversa?
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/y6_F_id88lo
EJERCICIO M2BE2040:
Determinar los valores de los parámetros a y b para los que tiene inversa la matriz:
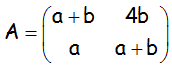
Calcular la matriz A-1 cuando a=3 y b=1.
VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/Ohz9ZCPxCus
EJERCICIO M2BE2245:
Dada la matriz A siguiente:
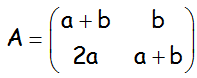
a.- ¿Para qué valores de a y b la matriz A no tiene inversa?
b.- Determinar la matriz inversa para el resto de valores.
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE2245 DE OBTENCIÓN DE LA MATRIZ INVERSA
EJERCICIOM2BE2956:
¿Cuándo la matriz A es regular (tiene inversa)? Si es posible, realiza la inversa para m = 2.

IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTE EJERCICIO: EXÁMENES RESUELTOS DE MATEMÁTICAS II, PARA 2º DE BACHILLERATO. ANÁLISIS DE FUNCIONES Y ÁLGEBRA. SEGUNDO TRIMESTRE 2024-25


