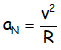OBTENCIÓN EXPRESIÓN ACELERACIÓN NORMAL

OBTENCIÓN DE LA EXPRESIÓN DE LA ACELERACIÓN NORMAL (MEDIDA DE LA VARIACIÓN DE LA DIRECCIÓN DE LA VELOCIDAD):OBTENCIÓN EXPRESIÓN ACELERACIÓN NORMAL

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:

ESTOS MATERIALES ESTÁN EN CONSONANCIA CON: 

COMPONENTES INTRÍNSECAS DE LA ACELERACIÓN:

Tengamos en cuenta que la ACELERACIÓN es «la variación de la velocidad», pero no podemos olvidar que la velocidad puede variar en DIRECCIÓN o en MÓDULO. La variación en módulo la cuantifica la ACELERACIÓN TANGENCIAL, y la variación en dirección la considera la ACELERACIÓN NORMAL.

Es por ello, por la doble posibilidad de variación de velocidad por lo que se hace necesario considerar dos aspectos dentro de la aceleración, que llamamos COMPONENTES INTRÍNSECAS DE LA ACELERACIÓN:

      • LA ACELERACIÓN TANGENCIAL: Es la variación del MÓDULO DE LA VELOCIDAD. 
      • LA ACELERACIÓN NORMAL: Es la variación de la DIRECCIÓN DE LA VELOCIDAD.

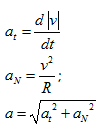
NOTAR COMO LA FÓRMULA DE LA ACELERACIÓN TANGENCIAL ES EVIDENTE, CONTANDO CON LA DEFINICIÓN DE «ACELERACIÓN TANGENCIAL» Y CON EL SENTIDO DE LA OPERACIÓN «DERIVADA» COMO VARIACIÓN. PARA LA EXPRESIÓN DE LA ACELERACIÓN NORMAL, LA COSA ES MÁS COMPLICADA, REQUERIENDO ESTE ARTÍCULO ESPECÍFICO PARA SU OBTENCIÓN.

OBTENCIÓN DE LA EXPRESIÓN DE LA ACELERACIÓN NORMAL:

Utilizaremos el siguiente movimiento circular uniforme, con lo que se consigue que la partícula no tiene aceleración tangencial (el movimiento es a velocidad constante en módulo). De este modo, cuando obtengamos algún tipo de aceleración, será la aceleración normal.

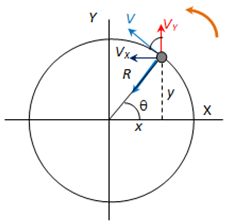
La partícula que se muestra realiza un movimiento circular a velocidad, en módulo, constante, según se indica, en el sentido de los ángulos positivos. Como esa velocidad va variando en dirección, el movimiento tiene aceleración, que a este tipo (relacionada con la variación de la velocidad en dirección –no en módulo-) se le denomina aceleración normal. Es la causante del movimiento circular en tanto que produce la fuerza que “tira” de la partícula hacia el centro de la circunferencia. Esa fuerza es la fuerza centrípeta. Tanto la aceleración normal, como la fuerza centrípeta están dirigidas hacia el centro del movimiento circular (dirección radial y hacia dentro).

La velocidad, que es tangente a la trayectoria es constante y la podemos descomponer en los ejes habituales, en una Vx y una Vy, según el dibujo.

El ángulo θ representado coincide con el ángulo que forma el vector velocidad con su componente en y.

Por ello y usando trigonometría:

Ya que la velocidad en x es negativa según el sistema de referencia.

Teniendo en cuenta que el ángulo θ forma parte del triángulo rectángulo representado, volviendo a usar trigonometría en este triángulo rectángulo:

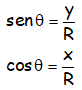
Con lo que las componentes de la velocidad:

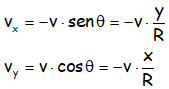
Teniendo además en cuenta que la aceleración es igual a la derivada de la velocidad con respecto al tiempo (la aceleración es la variación de la velocidad), nos queda para cada una de las componentes de la aceleración:

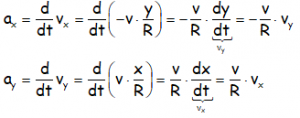
Ya que tanto la velocidad v como el Radio R son constantes en el Movimiento Circular uniforme (salen de la derivada) y además la derivada de y con respecto al tiempo es la velocidad en y, del mismo modo que la derivada de x con respecto al tiempo es la velocidad en x (la velocidad es la variación de la posición –la derivada de la posición-)

Si calculamos ahora el módulo de la aceleración, a partir de sus componentes:

Nos queda:

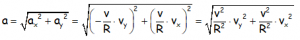
Que con el factor común y sacando de la raíz, al estar al cuadrado:

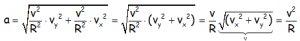
Ya que lo de dentro de la raíz es precisamente el módulo de la velocidad calculado a partir de sus componentes.

Con lo que nos queda, que esta aceleración, que es aceleración normal es:

Visualizaciones: 4
On: