TEOREMA DE ROUCHÉ:
PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
SIGUE EL ESQUEMA PLANTEADO PARA EL SEGUIMIENTO DE LA ASIGNATURA DE MATEMÁTICAS II DE 2º DE BACHILLERATO: MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
TEOREMA DE ROUCHÉ:
«La condición necesaria y suficiente para que tenga solución el sistema lineal, expresado de manera general:
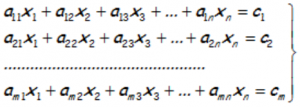
es que el rango de la matriz de los coeficientes (A), coincida con el rango de la matriz ampliada (A’) «
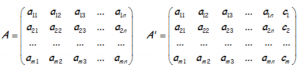
DEMOSTRACIÓN DEL TEOREMA DE ROUCHÉ:
El sistema general tiene solución si existen unos números x1, x2,…, xn que al ponerlos en cada una de las ecuaciones nos da el término independiente ci . Como se tiene que verificar esto para todas las ecuaciones al mismo tiempo, lo que se ha de verificar es la ecuación matricial:
Esto equivale a decir que la columna de los términos independientes (matriz C) es combinación lineal de las columnas de los coeficientes (A1,A2,…,An), ya que se obtiene multiplicando cada una de estas columnas por unos números, xi, por lo que C depende linealmente de las columnas A1,A2,…,An
Es por esto por lo que el rango de la matriz A de los coeficientes no varía al ampliarla con una nueva columna formada por la de los términos independientes (C).
Para ayudar a entenderlo, pensar que si el rango de A es menor que el rango de A’, la columna C no es combinación lineal de las columnas Ai, lo que nos indica que no existen unos números x1, x2,…, xn con los que conseguimos que se cumplan todas las ecuaciones.
El rango de A no puede ser mayor que el de A’, ya que A’ tiene una columna más, en cuyo caso o tienen el mismo rango o es A’ la que tiene el rango una unidad mayor.
TEOREMA DE ROUCHÉ-FRÖBENIUS:
Tener en cuenta que para que un sistema sea COMPATIBLE (tenga solución), el rango de la matriz de los coeficientes tiene que coincidir con el rango de la matriz ampliada (incluyendo la columna de los términos independientes); en caso contrario sería INCOMPATIBLE (sin soluciones).
Si además de la coincidencia de rangos entre las matrices de los coeficientes y la ampliada, el rango es igual al número de incógnitas, el sistema sería COMPATIBLE DETERMINADO (tendría una única solución). Si el valor de la coincidencia de rangos es inferior al número de incógnitas, el sistema sería COMPATIBLE INDETERMINADO (tendría infinitas soluciones). En este último caso, la diferencia entre el valor del número de incógnitas y el valor de la coincidencia de rangos nos daría el número de GRADOS DE LIBERTAD de las soluciones del sistema indeterminado (que no es sino el número de parámetros en función de los cuales aparecen las soluciones λ, μ…)


