COMPONENTES INTRÍNSECAS DE LA ACELERACIÓN: ACELERACIÓN NORMAL Y TANGENCIAL. CINEMÁTICA Y DINÁMICA PARA SECUNDARIA Y BACHILLERATO

COMPONENTES INTRÍNSECAS ACELERACIÓN DINÁMICA

COMPONENTES INTRÍNSECAS DE LA ACELERACIÓN: ACELERACIÓN NORMAL Y TANGENCIAL. CINEMÁTICA Y DINÁMICA PARA SECUNDARIA Y BACHILLERATO:

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:

• • LEYES DE NEWTON
  • DINÁMICA Y CINEMÁTICA PARA FÍSICA DE SECUNDARIA. LEYES DE NEWTON
  • UTILIZACIÓN DE LAS LEYES DE NEWTON EN EJERCICIOS DE DINÁMICA. FÍSICA DE SECUNDARIA Y BACHILLERATO
  • CANTIDAD DE MOVIMIENTO, MOMENTO LINEAL. TEOREMA DE CONSERVACIÓN. EJERCICIOS RESUELTOS
  • PROFUNDIZANDO EN LAS LEYES DE NEWTON

ESTOS MATERIALES ESTÁN EN CONSONANCIA CON: 

• • FÍSICA Y QUÍMICA DE 4º DE LA E.S.O.: DESARROLLO DE LA ASIGNATURA
  • FÍSICA Y QUÍMICA DE 1º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
  • FÍSICA DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA

COMPONENTES INTRÍNSECAS DE LA ACELERACIÓN:

Tengamos en cuenta que la ACELERACIÓN es «la variación de la velocidad», pero no podemos olvidar que la velocidad puede variar en DIRECCIÓN o en MÓDULO. La variación en módulo la cuantifica la ACELERACIÓN TANGENCIAL, y la variación en dirección la considera la ACELERACIÓN NORMAL.

Es por ello, por la doble posibilidad de variación de velocidad por lo que se hace necesario considerar dos aspectos dentro de la aceleración, que llamamos COMPONENTES INTRÍNSECAS DE LA ACELERACIÓN:

• LA ACELERACIÓN TANGENCIAL: Es la variación del MÓDULO DE LA VELOCIDAD. 
• LA ACELERACIÓN NORMAL: Es la variación de la DIRECCIÓN DE LA VELOCIDAD.

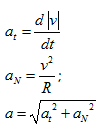
NOTAR COMO LA FÓRMULA DE LA ACELERACIÓN TANGENCIAL ES EVIDENTE, CONTANDO CON LA DEFINICIÓN DE «ACELERACIÓN TANGENCIAL» Y CON EL SENTIDO DE LA OPERACIÓN «DERIVADA» COMO VARIACIÓN. PARA LA EXPRESIÓN DE LA ACELERACIÓN NORMAL, LA COSA ES MÁS COMPLICADA, REQUERIENDO UN ARTÍCULO ESPECÍFICO PARA SU OBTENCIÓN.

• • • OBTENCIÓN DE LA EXPRESIÓN DE LA ACELERACIÓN NORMAL

EJEMPLOS QUE PUEDEN AYUDAR A ENTENDERLO MEJOR:

• • En movimientos rectilíneos, al no existir cambio en la dirección de la velocidad, sólo hay aceleración tangencial, NO TENDRÍA POR LO TANTO ACELERACIÓN NORMAL.
  • En un movimiento no rectilíneo (curvo, circular) aunque se mueva a velocidad constante, presenta aceleración (normal), independientemente de que tenga aceleración tangencial en el caso en que el valor en módulo de la velocidad no se mantenga constante.
  • En un movimiento circular uniforme, hay aceleración, sólo que es aceleración normal, ya que al ser uniforme no varía el módulo, el valor numérico de la velocidad. Pero al ser curvo, circular, la dirección de la velocidad está continuamente variando.

Tengamos en cuenta que DERIVADA=VARIACIÓN, lo que hace tan importante la herramienta matemática DERIVADA en física y en otras disciplinas como economía.

Si pensamos en la definición de aceleración instantánea como «derivada de la velocidad con respecto del tiempo», vemos claramente como DERIVADA=VARIACIÓN, idea que debemos tener siempre presente y acerca el concepto de «derivada» al mundo real.