ENCUENTRO ALCANCE MÓVILES CINEMÁTICA
RESOLUCIÓN DE EJERCICIOS DE ENCUENTRO DE MÓVILES, DE ALCANCE DE MÓVILES CON MRU Y MRUA:

PODRÍA INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
Las estrategias básicas para resolver estos ejercicios de encuentro, de alcance de móviles, podrían resumirse en estos 4 pasos:
1.- Identificar los tipos de movimientos (MRU,MRUA, CAÍDA LIBRE) de cada uno de los móviles que participan en el problema.
2.- Expresar la ecuación del movimiento de cada uno de ellos (la ecuación del espacio de la POSICIÓN) de cada uno de ellos. (tener en cuenta las posiciones iniciales de cada uno)
3.- Igualar las ecuaciones de la posición (ya que en el encuentro, en el alcance, las posiciones de los dos son la misma).
4.- Tener en cuenta las relaciones entre los tiempos de cada uno (podría no ser el mismo) si inician su movimiento en instantes diferentes.
Lo que normalmente obtenemos en primer lugar es el tiempo en el que se produce el alcance de los móviles, que puesto en cualquiera de las dos ecuaciones de la posición, nos dice el lugar donde se produce el encuentro.
Una de las DIFICULTADES frecuentes es la relativa al TIEMPO. En ocasiones el tiempo en el que alguno de ellos comienza el movimiento no es el mismo que el tiempo en el que la inicia el otro.
Es frecuente que nos digan algo parecido a “dos segundos más tarde otro móvil inicia el movimiento”, con lo que tenemos que considerar esta diferencia de tiempo:
Debemos tener en cuenta que en un caso como éste, para uno de los móviles el tiempo es “t”, mientras que para el otro el tiempo es “t-2” (para el que arranca más tarde).
Otra de las DIFICULTADES es el SENTIDO en el que se mueven, si los dos van en el mismo sentido, ningún problema; pero si uno se mueve en sentido contrario al otro habrá que definir bien las velocidades, ya que una de ellas será negativa.
Respecto a las POSICIONES INICIALES, como suele ocurrir que estén separados una cierta distancia hay que tener bien presente la posición inicial de cada uno de ellos, tomando la posición inicial de alguno como cero y la del otro la que corresponda según este criterio.
EJEMPLOS RESUELTOS DE DIFERENTES CASOS:
LOS DOS MÓVILES CON MRU, EN LA MISMA DIRECCIÓN Y SENTIDO, SEPARADOS UNA DISTANCIA, QUE SALEN AL MISMO TIEMPO:
EJERCICIO FQ1B1886:
Una bicicleta que se mueve con velocidad constante de 8 m/s sale de un punto A. En el mismo instante, desde un punto B situado a 200 metros de A, en la misma dirección y sentido, inicia el movimiento un peatón con velocidad de 1,5 m/s. ¿En qué momento y a qué distancia de B se produce el encuentro?
RESOLUCIÓN DEL EJERCICIO:
MÓVIL A: Lleva un MRU (Movimiento Rectilíneo Uniforme), con velocidad de 8 m/s. Consideramos para él que su posición inicial es cero. Su velocidad positiva (igual que la de B –mismo sentido-). Para los dos móviles el tiempo es el mismo.
La Ecuación del Movimiento MRU:
Para este móvil A:
MÓVIL B: Lleva tambien un MRU (Movimiento Rectilíneo Uniforme), con velocidad de 1,5 m/s. Consideramos para él que su posición inicial es 200 m (separado del origen elegido de posiciones que es A). Su velocidad positiva (igual que la de A –mismo sentido-). Para los dos móviles el tiempo es el mismo.
Para este móvil B:
En el encuentro, las dos posiciones son la misma, por ello:
Como nos dicen que los dos salen en el mismo instante: tA = tB = t
Con lo que:
Este tiempo puesto en cualquiera de las dos ecuaciones del movimiento, por ejemplo en la primera:
El encuentro se produce a 246,16 metros del punto A, es decir a 46,16 m del punto B.
EJERCICIO FQ4E1312:
Un coche sale de A con velocidad constante de 70 Km/h. Al mismo tiempo de B, situado a un km de A en la misma dirección y sentido sale una bicicleta con velocidad igualmente constante de 25 km/h.
a) ¿En qué momento se producirá el encuentro?
b) ¿A qué distancia de B?
RESOLUCIÓN DEL EJERCICIO:
Las velocidades son ambas positivas, consideramos sentido positivo hacia la derecha.
Consideramos igualmente el origen de los espacios en A;
A parte de x0 = 0 m; B tiene x0 = 1000 m
En el momento del encuentro, las posiciones de los dos:
A: MRU:
B: MRU:
En el encuentro: xA = xB
Con lo que:
Se encontrarán a los 89,21 s de partir los dos, cada uno de ellos.
Sustituyendo este tiempo en cualquiera de las ecuaciones (en B por ejemplo):
Se encontrarán en la posición 1735,1 m, es decir a 735 m de B.
LOS DOS MÓVILES SE MUEVEN CON MRU, EN LA MISMA DIRECCIÓN Y SENTIDO, SEPARADOS UNA DISTANCIA, PERO SALEN EN TIEMPOS DIFERENTES:
EJERCICIO FQ1B1887:
En Valsequillo, en Gran Canaria, un corredor que se mueve con velocidad constante de 4 m/s sale de un punto A pretendiendo saludar a un senderista que está descansando a 150 metros de distancia. Dos segundos más tarde, el senderista (que no ve el interés del corredor en saludarlo) inicia su paseo, en la misma dirección y sentido que el corredor, a una velocidad constante de 1 m/s. ¿En qué momento y a qué distancia del lugar de descanso del senderista se produce el encuentro?
RESOLUCIÓN DEL EJERCICIO:
CORREDOR (MÓVIL A): Lleva un MRU (Movimiento Rectilíneo Uniforme), con velocidad de 4 m/s. Consideramos para él que su posición inicial es cero. Su velocidad positiva (igual que la del senderista –mismo sentido-).
La Ecuación del Movimiento MRU, para este móvil A:
SENDERISTA (MÓVIL B): Lleva también un MRU (Movimiento Rectilíneo Uniforme), con velocidad de 1 m/s. Consideramos para él que su posición inicial es 150 m (separado del origen elegido de posiciones que es A). Su velocidad positiva (igual que la de A –mismo sentido-). La Ecuación del Movimiento MRU:
Para este móvil B:
En el encuentro, las dos posiciones son la misma, por ello: xA = xB
Como nos dicen que el senderista inicia el movimiento dos segundos más tarde, podemos asignar los siguientes tiempos:
Pensar que el senderista está moviéndose dos segundos menos que el corredor (inicia el movimiento más tarde).
Del mismo modo podríamos considerar:
Ya que el corredor está moviéndose dos segundos más (inicia el movimiento dos segundos antes). Daría lo mismo, pero para la resolución del ejercicio nos vamos a quedar con la primera de las opciones:
Teniendo esto en cuenta:
Este tiempo es el de A, con lo que debemos ponerlo en su ecuación, en la del corredor. Si quisiéramos ponerlo en la ecuación del senderista, tendríamos que restarle los dos segundos.
El encuentro se produce a 197,32 metros del punto A, es decir a 47,32 m del lugar de descanso del senderista.
LOS DOS MÓVILES CON MRU, EN LA MISMA DIRECCIÓN Y SENTIDOS CONTRARIOS, SEPARADOS UNA DISTANCIA, QUE SALEN AL MISMO TIEMPO:
EJERCICIO FQ1B1888:
Dos enamorados, separados una distancia de 150 metros, acuden uno al encuentro del otro. Él con una velocidad constante de 5 metros por segundo y ella con una velocidad de 5,5 m/s. Si los dos inician el movimiento al mismo tiempo ¿En qué momento y en qué lugar entre ellos se produce el encuentro?
RESOLUCIÓN DEL EJERCICIO:
Notar como el dibujo representa la situación. Hemos llamado x a la distancia entre ella y el lugar donde se produce el encuentro. Tomaremos como origen de posiciones, la posición de ÉL.
ÉL (MÓVIL A): Lleva un MRU (Movimiento Rectilíneo Uniforme), con velocidad de 5 m/s. Consideramos para él que su posición inicial es cero. Su velocidad la consideraremos positiva, acorde con el sistema de referencia habitual y el dibujo que hemos elegido para representar la situación.
La Ecuación del Movimiento MRU, para este móvil A:
ELLA (MÓVIL B): Lleva tambien un MRU (Movimiento Rectilíneo Uniforme), con velocidad de 5,5 m/s. Consideramos para él que su posición inicial es 150 m (separado del origen elegido de posiciones que es A). Su velocidad ES NEGATIVA, ya que es de sentido contrario a la velocidad elegida como positiva, la de él.
La Ecuación del Movimiento MRU, para este móvil B:
En el encuentro, las dos posiciones son la misma, por ello:
Como nos dicen que los dos inician el movimiento al mismo tiempo: tA = tB = t
Teniendo esto en cuenta:
Este tiempo puesto en cualquiera de las dos ecuaciones, nos dará la posición a la que se produce el encuentro. Puesta en la primera de ellas:
El encuentro se produce a 71,4 metros de él. Más cerca de él puesto que ella lleva más velocidad.
EJERCICIO FQ4E1313:
Un coche sale de A con velocidad constante de 65 Km/h. Al mismo tiempo desde un punto B, situado a 3 Km de A en la misma dirección y sentido opuesto sale un peatón con velocidad igualmente constante de 3 km/h.
a) ¿En qué momento se producirá el encuentro?
b) ¿A qué distancia de A?
RESOLUCIÓN DEL EJERCICIO:
El diagrama de la situación:
Las velocidades son de diferente signo, consideramos sentido positivo hacia la derecha, negativa la velocidad de B. A parte del origen de los espacios, de A. B desde la posición inicial xo=3000 m.
Las ecuaciones del movimiento de ambos móviles:
en el momento del encuentro xA= xB
Sustituyendo este tiempo en cualquiera de las dos ecuaciones:
Se encontrarán a 2875,7 m de A
UN MÓVIL CON MRU, EL OTRO CON MRUA EN LA MISMA DIRECCIÓN Y SENTIDO, SEPARADOS UNA DISTANCIA, QUE SALEN EN TIEMPOS DIFERENTES:
EJERCICIO FQ1BE1787:
Un vehículo circula por una carretera de visibilidad reducida por niebla (no podemos ver más allá de 100 m) a 80 km/h.
En un instante determinado el conductor del vehículo vé un atasco en el que la caravana circula a 25 km/h. Si el conductor tarda un segundo y medio en reaccionar y pulsar el freno, con el que se comunica a las ruedas una aceleración de frenado de 5 m/s2, ¿chocará contra la caravana o saldrá ileso?
RESOLUCIÓN DEL EJERCICIO:
Llamando v0=80 km/h la velocidad a la que circula el vehículo (notar que durante 1,5 segundos que tarda en reaccionar, el vehículo lleva un MRU, que lo acerca aún más a la caravana). No olvidar que la caravana se sigue moviendo.
Llamando v2=25 km/h a la velocidad de la caravana (también MRU)
Pasando estas velocidades a m/s.
Teniendo en cuenta que como la visibilidad se limita a 100 m, cuando el conductor ve el atasco se encuentra a 100 metros de él.
Las ecuaciones del movimiento del vehículo:
En el primer segundo y medio, que lleva MRU, ha recorrido:
Un esquema de la situación (complicada de entender):
Por entender mejor el esquema:
Cuando el vehículo pasa de A a B con MRU, la caravana ha pasado de C a C ’,
Y cuando el vehículo en B comienza a frenar con intención de parar, con M.R.U.Desacelerado, la caravana pasará de C ’ a C ’’, que es donde se encuentra la caravana cuando el vehículo ya se ha parado en B’.
A partir de 1,5 segundos, el vehículo lleva un MRUA, con velocidad inicial de 22,2 m/s; con aceleración a=-5m/s2, con la que pretendemos parar el vehículo (velocidad final cero). La ecuación correspondiente a este movimiento, desde el comienzo en A (notar como vamos a considerar x0=33,3 m, para no tener que sumarle esta cantidad después:
Como pretendemos parar el vehículo, su velocidad final es cero, con lo que el tiempo en pararse:
Con la ecuación del movimiento del vehículo y este tiempo:
Con este resultado está clarísimo que no choca, ya que no llega a los 100 m a los que se encontraba el atasco (además tener en cuenta que la caravana sigue en movimiento con lo que todavía estará más alejada de los 100 m)
OTRA MANERA DE RESOLVERLO, MÁS «PROFESIONAL»:
La manera más profesional de hacer ejercicios de ENCUENTRO DE MÓVILES, es igualar las ecuaciones del movimiento de los dos móviles (ya que si se encuentran, en ese momento tienen la misma posición, la misma x). En este ejercicio la complicación que se tiene que tener en cuenta es que el MRUD del vehículo se inicia 1,5 segundos más tarde de iniciarse el tiempo.
La ecuación del movimiento del vehículo:
La ecuación de movimiento de la caravana, teniendo en cuenta que su posición inicial son los 100 metros que lo separan del coche, y su tiempo es t.
Igualando:
Que no tiene solución, al resolver la ecuación de segundo grado da negativo lo de dentro de la raiz, indicándonos, que no se encuentran para ningún tiempo, lo mismo que nos había indicado la otra forma de resolverlo.
UN MÓVIL CON MRU, EL OTRO CON MRUA EN LA MISMA DIRECCIÓN Y SENTIDOS CONTRARIOS, SEPARADOS UNA DISTANCIA, QUE SALEN EN TIEMPOS DIFERENTES:
EJERCICIO FQ4E1314:
Un vehículo parte del reposo, con una aceleración de 1 m/s2 de un punto A. Cinco segundos más tarde desde un punto B, situado a 500 m de A en la misma dirección y sentido sale una bicicleta con velocidad constante de 20 km/h.
a) ¿En qué momento se producirá el encuentro?
b) ¿Cuánto ha recorrido cada móvil hasta que se encuentran?
RESOLUCIÓN DEL EJERCICIO:
-
- Tener en cuenta que: tA – 5 = tB (B está moviéndose 5 segundos menos).
- Las velocidades son ambas positivas, consideramos sentido positivo hacia la derecha.
- Consideramos igualmente el origen de los espacios en A: A parte del origen y B tiene una posición inicial de 500 m.
En el encuentro ambos estarán en la misma posición (xA=xB), teniendo en cuenta que: tA – 5 = tB ; si consideramos además que: tA = t y que tB = t – 5 , nos evitamos el cuadrado de la suma.
Con todo ello:
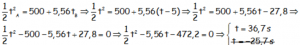
a) Se encontrarán a los 36,7 s de partir A y a los 31,7 de partir B
b) Al sustituir este tiempo en cualquiera de las dos ecuaciones del movimiento, obtenemos que se encontrarán en la posición 676,25 m.
A ha recorrido 676,25 m; B ha recorrido 176,25 m
OTROS EJERCICIOS CON SOLUCIÓN DE ENCUENTRO DE MÓVILES (FQ1BP326):
Las soluciones se muestran a continuación de la relación, para motivar la búsqueda de la misma sin su consulta inicial.
1. Una piedra de 1 Kg se deja caer desde un acantilado de 10 m. de altura. En el mismo instante se lanza hacia arriba desde la base del acantilado una pelota con una velocidad inicial de 15 m/s.
a) ¿Qué tiempo habrá transcurrido cuando se encuentren?
b) ¿Al encontrarse, está todavía ascendiendo la pelota?
c) Si la piedra tuviera un peso de 2 Kg. ¿Cuál sería la respuesta del apartado a)? ¿Por qué‚?
2. Un tornillo se desprende del fondo de un ascensor que se mueve hacia arriba con una velocidad de 6 m/s. El tornillo llega al fondo del hueco del ascensor en 3 s.
a) ¿A qué altura estaba el ascensor cuando se desprendió el tornillo?
b) ¿Cuál es la velocidad del tornillo al chocar contra el fondo del hueco del ascensor?
3. Un punto A se encuentra en la misma vertical que otro punto B y a 60 m de altura sobre éste. Desde A se deja caer un cuerpo sin velocidad inicial. Dos segundos después se lanza, desde B, otro cuerpo con una velocidad inicial de 20 m/s, verticalmente hacia arriba. ¿En qué punto chocarán ambos cuerpos?
4. Un tren se está moviendo a 72 km/h cuando una lámpara que está colgada en el extremo del tren a 5 m del piso, se suelta. Calcular la distancia recorrida por el tren en el tiempo que tarda la lámpara en caer al suelo. ¿Dónde cae la lámpara con respecto al tren y a los rieles? ¿Cuál es la trayectoria con respecto al tren y a los rieles?
5. Un niño sentado en un vagón de ferrocarril, que se mueve con velocidad constante, lanza una pelota directamente hacia arriba. ¿Caerá la pelota detrás de él, delante de él, en sus manos?
6. Un hombre corre con la mayor velocidad que puede, 6 m/s, para alcanzar un tren que está a punto de partir. Cuando se encuentra en el andén a 32 m de la escalerilla del último vagón, el tren arranca con una aceleración constante de 0,5 m/s2. ¿Conseguirá el hombre alcanzar al tren?
7. Una pelota se lanza desde el suelo hacia arriba. Al cabo de un segundo ha recorrido 25 m. Hallar:
a) la velocidad inicial.
b) la altura máxima alcanzada.
8. Dos ciudades A y B distan entre sí 400 km. Desde la ciudad A parte un móvil con una velocidad cuyo módulo es de 80 km/h hacia la ciudad B, desde la ciudad B parte un móvil con velocidad cuyo módulo es de 120 km/h hacia la ciudad A. ¿En qué momento y a que distancia de la ciudad A se produce el encuentro?
SOLUCIONES DE ESTA RELACIÓN DE EJERCICIOS:
1. 2/3 s. ;
2. 27 m; -24 j (m/s)
3. a 45 m de A y 15 de B
4. 20 m
6. Sí
7. v = 30 i m/s; h = 45 m.
8. 2 H, 160 km de A
