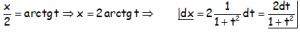DEMOSTRACIÓN SUSTITUCIÓN UNIVERSAL INTEGRALES
DEMOSTRACIÓN DE LAS EXPRESIONES DE LA «SUSTITUCIÓN UNIVERSAL» EN INTEGRALES TRIGONOMÉTRICAS:
PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- MÉTODOS DE INTEGRACIÓN PARA INTEGRALES TRIGONOMÉTRICAS
- EJERCICIOS RESUELTOS DE INTEGRALES TRIGONOMÉTRICAS
- CÁLCULO DE INTEGRALES PARA MATEMÁTICAS DE BACHILLERATO
- MÉTODO DE INTEGRACIÓN POR SUSTITUCIÓN O CAMBIO DE VARIABLE. EJEMPLOS RESUELTOS
- EJERCICIOS RESUELTOS DE INTEGRALES POR SUSTITUCIÓN O CAMBIO DE VARIABLE PARA MATEMÁTICAS DE 2º DE BACHILLERATO
- MÉTODO DE INTEGRACIÓN POR PARTES DE RESOLUCIÓN DE INTEGRALES PARA BACHILLERATO
- INTEGRACIÓN DE FUNCIONES RACIONALES
SIGUE EL PROCESO DETERMINADO POR:
- MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
- Y PUEDE TENER UTILIDAD EN: AYUDANDO A NUESTROS ALUMNOS QUE ESTÁN EN LA UNIVERSIDAD
ECUACIONES CORRESPONDIENTES A LA SUSTITUCIÓN UNIVERSAL EN INTEGRALES RACIONALES TRIGONOMÉTRICAS:
Las ecuaciones que resultan, al utilizar la sustitución:
![]()
en las integrales trigonométricas que responden al modelo:
![]()
en el que las expresiones seno, coseno y dt se sustituyen en expresiones que pueden resultar convenientes en la mayoría de los casos, son las siguientes:
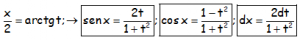
Que intentaremos obtener a modo de comprobación-demostración de las mismas, si se tiene ese interés educativo:
Para la expresión del sen x, tenemos que partir del seno del ángulo doble y continuar con los procesos indicados:
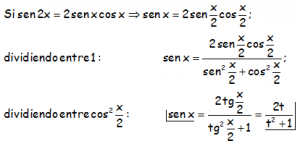
Para la expresión del cos x, tenemos que partir del coseno del ángulo doble y continuar con los procesos indicados:
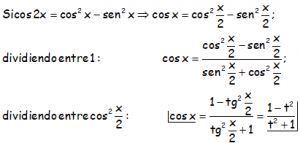
Para la expresión del dt, seguimos el siguiente proceso: