MÁXIMOS MÍNIMOS PUNTOS INFLEXIÓN
CRITERIO DEFINITIVO PARA DISTINGUIR MÁXIMOS, MÍNIMOS Y PUNTOS DE INFLEXIÓN. PUNTOS DONDE LA DERIVADA SE ANULA:

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
Este artículo se elabora en el contexto en el que existen puntos en los que la primera derivada vale cero que no son Máximos ni mínimos sino puntos de Inflexión.
Esto ocurre cuando se presenta la situación en la que las derivadas primera, segunda, incluso siguientes son cero y aquí se expone la manera de saber si se trata de Máximos, Mínimos o si son incluso Puntos de Inflexión.
Tendemos a pensar que si la derivada en un punto (si la primera derivada en un punto) es cero tenemos un máximo o mínimo y no siempre es cierto. Lo único realmente cierto, es que si la primera derivada es cero en un punto, en ese punto la función tiene una recta tangente horizontal, con pendiente cero. Cuando en un punto en el que la derivada vale cero no tenemos un máximo o mínimo, lo que nos encontramos es con un punto de inflexión con tangente horizontal.
En primer lugar, debemos establecer claramente qué es para nosotros un tramo de función cóncava y del mismo modo, convexa.
Es posible encontrar textos que consideran estas dos cualidades de manera diferente. En tres dimensiones no hay ninguna duda; por ejemplo en una cuchara la parte de la cuchara donde se deposita la sopa es cóncava y la de detrás convexa. Con las funciones debemos definir exactamente desde donde las vamos a mirar: si desde arriba o desde abajo.
En lo que sigue, para nosotros, cóncavo es «∪», y convexo es «∩». Estamos mirando las funciones desde arriba. Otros profesores o textos dicen «cóncavo hacia arriba» para «∪», y cóncavo hacia abajo para «∩».
Los criterios habituales de presencia de máximo, mínimo y puntos de inflexión, que son los necesarios en la mayoría de los casos que se nos presentan en ejercicios:
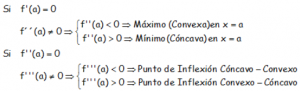
Pero puede ocurrir en ejercicios de algo más de nivel, que siendo la primera derivada cero, las siguientes derivadas: segunda, tercera… sigan dando cero hasta que dejan de ser igual a cero en una de ellas; el criterio para distinguir entonces si el punto es cuestión es un máximo, un mínimo o un punto de inflexión es:
Si f ‘(a) = f »(a) = f »'(a) = … = f n-1(a) = 0 y f n(a) ≠ 0
Si n es impar, tenemos un Punto de Inflexión con tangente horizontal, con las siguientes particularidades:
Si f n(a) < 0 , entonces tenemos un Punto de Inflexión Cóncavo-Convexo.
Si f n(a) > 0 , entonces tenemos un Punto de Inflexión Convexo-Cóncavo.
Si n es par, tenemos un Máximo o un Mínimo:
Si f n(a) < 0 , entonces tenemos un Máximo (función Convexa).
Si f n(a) > 0 , entonces tenemos un Mínimo (función Cóncava).
Para que quede algo más claro, veamos los siguientes ejemplos en los que se registran estas situaciones, con funciones polinómicas sencillas de diferentes grados. Se aporta la representación gráfica para confirmar lo que se va obteniendo analíticamente:
EJEMPLO CON FUNCIÓN POLINÓMICA DE SEGUNDO GRADO:
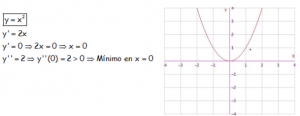
EJEMPLO CON FUNCIÓN POLINÓMICA DE TERCER GRADO:
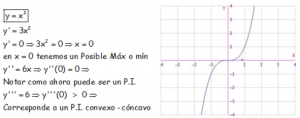
EJEMPLO CON FUNCIÓN POLINÓMICA DE CUARTO GRADO:
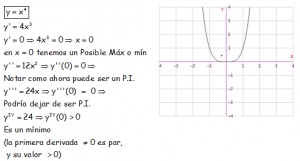
EJEMPLO CON FUNCIÓN POLINÓMICA DE QUINTO GRADO:
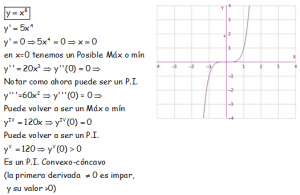
Ahora estaría muy bien, como ejercicio, confirmar todo esto haciendo lo mismo con:
a.- f(x) = – x2
b.- f(x) = – x3
c.- f(x) = – x4
d.- f(x) = – x5
