EJERCICIOS RESUELTOS INTEGRALES RACIONALES
EJERCICIOS RESUELTOS DE INTEGRALES RACIONALES:
PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- INTEGRACIÓN DE FUNCIONES RACIONALES
- CÁLCULO DE INTEGRALES PARA MATEMÁTICAS DE BACHILLERATO
- MÉTODO DE INTEGRACIÓN POR SUSTITUCIÓN O CAMBIO DE VARIABLE. EJEMPLOS RESUELTOS
- EJERCICIOS RESUELTOS DE INTEGRALES POR SUSTITUCIÓN O CAMBIO DE VARIABLE PARA MATEMÁTICAS DE 2º DE BACHILLERATO
- MÉTODO DE INTEGRACIÓN POR PARTES DE RESOLUCIÓN DE INTEGRALES PARA BACHILLERATO
- EJERCICIOS RESUELTOS DE INTEGRALES POR PARTES
- MÉTODOS DE INTEGRACIÓN PARA INTEGRALES TRIGONOMÉTRICAS
- MÉTODO DE INTEGRACIÓN PARA INTEGRALES IRRACIONALES. CÁLCULO INTEGRAL
SIGUE EL PROCESO DETERMINADO POR:
Y puede formar parte de: AYUDANDO A NUESTROS ALUMNOS QUE ESTÁN EN LA UNIVERSIDAD
EJERCICIO M2BE3241:
Resolver la siguiente integral:
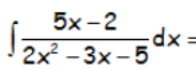
RESOLUCIÓN DEL EJERCICIO:
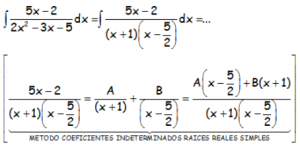
Identificando numeradores, ya que los denominadores son iguales:
![]()
Para encontrar los valores de A y B que cumplen esta realidad, podemos darle valores “convenientes” a la x, de tal modo que:
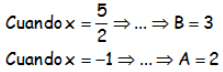
Con lo que ya podemos transformar la integral en suma de integralitas que serán logaritmos neperianos:
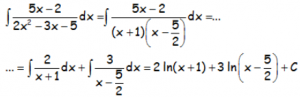
EJERCICIO M2BE3242:
Resolver la siguiente integral:
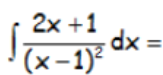
RESOLUCIÓN DEL EJERCICIO:
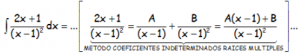
Identificaríamos los numeradores, igual que en el caso anterior y los valores convenientes en este caso sólo tenemos uno: x=1, con lo que una vez calculado B con este valor, hay que sustituirlo y tomar por ejemplo x=0 para hallar el valor de A.
Cuando hacemos esto, nos queda A=2; B=3, con lo que nos quedan dos integrales, un logaritmo neperiano y una potencial que se puede resolver por sustitución por ejemplo:

EJERCICIO M2BE117A:
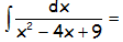
RESOLUCIÓN DEL EJERCICIO:
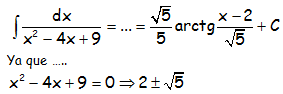
PROPONEMOS LA SIGUIENTE RESOLUCIÓN ALTERNATIVA, MÁS «IMAGINATIVA», DE ÉSTA Y OTRAS INTEGRALES RACIONALES CON DENOMINADOR DE RAÍCES IMAGINARIAS: EJERCICIOS RESUELTOS DE INTEGRALES RACIONALES CURIOSAS QUE TERMINAN EN ARCOTANGENTE
EJERCICIO M2BE117C:
Resolver la siguiente integral indefinida:
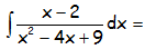
RESOLUCIÓN DEL EJERCICIO:
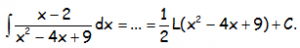
EJERCICIO M2BE118C:
Resolver la siguiente integral indefinida:
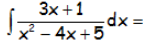
RESOLUCIÓN DEL EJERCICIO:
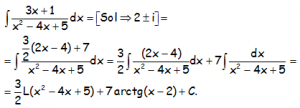
EJERCICIO M2BE3243:
Resolver la siguiente integral indefinida:
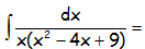
RESOLUCIÓN DEL EJERCICIO:
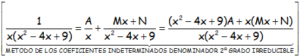
Notar el numerador de la fracción con denominador irreducible por tener raíces imaginarias.
Identificando numeradores y tomando valores para la x (son necesarios tres valores diferentes; uno de ellos x=0, los otros dos los que se desee), se obtiene:
![]()
Con lo que:



