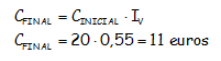ENCADENAMIENTOS PORCENTUALES ÍNDICE VARIACIÓN
ENCADENAMIENTOS PORCENTUALES CON EL ÍNDICE DE VARIACIÓN:
PODRÍA INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- REGLA DE TRES DIRECTA
- REGLA DE TRES INVERSA
- REGLA DE TRES COMPUESTA. PROPORCIONALIDAD COMPUESTA
- ÍNDICE DE VARIACIÓN PARA OBTENCIÓN DE PORCENTAJES
Cuando a una determinada cantidad se le aplican sucesivos porcentajes, bien de aumentos o disminución, la fórmula del ÍNDICE DE VARIACIÓN,
CFINAL = CINICIAL · IV
simplifica muchísimo las cosas, ya que en los encadenamientos porcentuales el Índice de Variación es el producto de los índices de variación de los sucesivos porcentajes encadenados.
Imaginemos el siguiente EJERCICIO:
EJERCICIO M3EE3300:
Un comerciante compra a su proveedor un ordenador portátil por 310 euros, pretende obtener un beneficio al venderlo del 30 %. Este ordenador no encuentra a ese precio comprador, por lo que en el período de rebajas, le aplica una descuento del 20%. ¿Cuál es el precio final de venta?.
RESOLUCIÓN:
En clase es frecuente que ante este problema el alumno, directamente aplique a los 310 euros el 10 %, que es la diferencia entre el 30 % de subida y el 20 % de bajada, lo cual es erróneo aunque no deja de ser inicialmente bastante lógico.
El proceso paso a paso si por ejemplo utilizamos la regla de tres:

El vendedor al aplicarle al ordenador un 30% de aumento lo pone inicialmente en venta por:
310+93=403 euros
Posteriormente llegan las rebajas y le aplica un descuento del 20%. Para calcular el precio al que se queda después de este descuento, con la regla de tres:

El comprador, pondrá una nueva etiqueta al ordenador con el nuevo precio:
403-80,6=322,4 euros.
Notar como con este proceso hemos tenido que hacer dos reglas de tres y una suma y una resta.
Si utilizamos la fórmula:
CFINAL = CINICIAL · IV
Teniendo en cuenta que:
para el aumento del 30 % el índice de variación es de 1,30
para el descuento del 20 % el índice de variación es de 0,8
El índice de variación de todo el proceso considerado conjuntamente es de 1,3 · 0,8 .
Por ello:
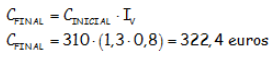
Caer en la cuenta de lo mucho que se simplifica el cálculo de la cantidad final asociada a encadenamientos porcentuales utilizando esta fórmula y el ÍNDICE DE VARIACIÓN.
Por otro lado y respecto al error lógico de considerar que subir un 30% y bajar un 20% es como si fuera subir un 10%, veamos:
El 10% de aumento sobre la cantidad inicial, también con índice de variación:
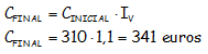
Cantidad diferente de la que nos ha dado. Esto ocurre porque el 20 % de descuento no se aplica sobre la cantidad inicial, sino sobre la cantidad aumentada.
EJERCICIO M3EE3301:
Cuánto dinero me queda en la cuenta al poner 3000 euros al 3% anual durante 2 años.
RESOLUCIÓN:
La fórmula que nos da el capital final (CF) que tenemos después de depositar un número n de años un determinado capital inicial (C) al r% de interés anual es, en función del ÍNDICE DE VARIACIÓN:

Teniendo en cuenta que para un interés del 3% el Índice de Variación de igual a 1,03
EJERCICIO M3EE3302:
Hallar el precio final de un artículo que cuesta 17 euros si tiene un 20 % de descuento.
RESOLUCIÓN:
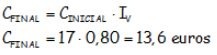
Ya que el Índice de Variación para un descuento del 20% es de 0,8
EJERCICIO M3EE3303:
¿En cuánto se me queda un producto que cuesta 7 euros si tiene un 12 % de I.V.A.?
RESOLUCIÓN:

Ya que el índice de variación asociado a un incremento del 12% es de 1,12.
EJERCICIO M3EE3304:
Compro para venderla en ebay una play por 300 euros. Le subo un 15 % y como no se vende le hago un descuento del 10 %. ¿En cuándo se queda y cuánto gano?.
RESOLUCIÓN:
Al hacerle un aumento del 15% al precio inicial de 300 euros (el índice de variación es de 1,15):

Si posteriormente a este precio le hago un descuento del 10% (índice de variación es 0,9)
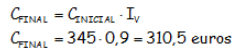
Este resultado podía haberse obtenido considerando los porcentajes encadenados con el índice de variación compuesto por 1,15 y 0,90, de un solo golpe.
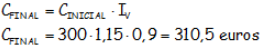
Por ello, el precio final es de 310,5 euros y la ganancia ha sido de 10,5 euros
EJERCICIO M3EE3305:
Tengo 20 euros y gasto en golosinas un 15 %. En el Pat Donald un 30 % ¿Cuánto me sobra?
RESOLUCIÓN:
Está claro que gastas un 45% del dinero que tienes, con lo que, teniendo en cuenta que el índice de variación en este caso es de 0,55: