INTERÉS COMPUESTO ÍNDICE VARIACIÓN
INTERÉS COMPUESTO UTILIZANDO EL ÍNDICE DE VARIACIÓN:
PODRÍA INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- REGLA DE TRES DIRECTA
- REGLA DE TRES INVERSA
- REGLA DE TRES COMPUESTA. PROPORCIONALIDAD COMPUESTA
- ÍNDICE DE VARIACIÓN PARA OBTENCIÓN DE PORCENTAJES
La fórmula que nos da el capital final (CF) que tenemos, después de depositar un número n de años, un determinado capital inicial (C), al r% de interés anual es, en función del ÍNDICE DE VARIACIÓN:
CFINAL = CINICIAL · (IV)n
Que es la misma, que expresada en forma de INTERÉS COMPUESTO:

EJERCICIO M3EE3306:
¿En cuánto se transforma un capital del 3000 euros colocado al 3,5% anual durante un año?
RESOLUCIÓN:
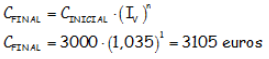
EJERCICIO M3EE3307:
¿En cuánto se transformaría la misma cantidad de 3000 euros colocado al mismo 3,5 % anual, después de dos años?
RESOLUCIÓN:
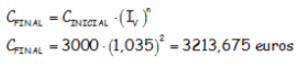
Últimamente se está poniendo al uso que los bancos paguen intereses mensuales. Basándonos en el mismo ejemplo I:
EJERCICIO M3EE3308:
¿En cuánto se transforma un capital de 3000 euros colocado al 3,5 % anual, durante un año, en una cuenta de ahorro que paga intereses mensuales?
RESOLUCIÓN:
El 3,5 % anual, supone un:
![]()
Que corresponde a un índice de variación de 1,002916.
Que estaría colocado durante 12 meses. Por ello el modo de obtener el capital final:
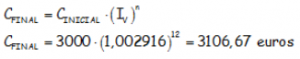
Sólo ligeramente superior (un euro y medio) que el resultado obtenido en el ejemplo I de pago de intereses anuales.
Notar como en el redondeo, hemos hecho a la baja, como los bancos, supongo.


