NÚMEROS DECIMALES, OPERACIONES:

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS:
SIGUE EL ESQUEMA DETERMINADO POR LA PROPUESTA DE PROGRAMACIÓN DE MATEMÁTICAS PARA 1º DE LA E.S.O.:
Los números decimales son números no enteros que se componen de una parte entera y una parte decimal, separadas por una coma. Por ejemplo: 82, 34
La parte entera es 82 que representa unidades enteras y completas y el 34 es la parte decimal que representa fracciones de la unidad. Concretamente en este ejemplo son 34 centésimas de la unidad, ya que a la derecha de la coma, la cifras son: décimas (primera posición a la derecha de la coma), centésimas (segunda posición a la derecha de la coma), y sucesivamente, milésimas, diez milésimas…
En ocasiones es necesario para mayor exactitud en la medición, se trate de lo que se trate.
Los números decimales pueden ser finitos como el 0,25
Con 0,25 representamos la cuarta parte, la división 1/4 ó 1:4.
O infinitos como el 1,333333333…. ó 4,1666666666….
Que resulta de la división 4/3 para el 1,3333333….. ó de la división 25/6 para el 4,16666666….
Estos dos números infinitos y que se repiten los números de la parte decimal: decimos que son números decimales periódicos, ya que en el 1,33333333….. se repite el 3, siendo precisamente el 3 el periodo, que se representa con un sombrerillo curvo. El 4,166666…. se repite el 6:
![]()
También hay números decimales infinitos, pero que no son periódicos, y son consecuencia de operaciones como la siguiente, la raíz cuadrada de 2.
![]()
que se observa que no existe una repetición de los decimales que se obtienen. Se muestran 25 decimales pero hay infinitos. O por ejemplo el número π, o el número de Euler «e»
π = 3,1415926535897932384626433…
e = 2,7182818284590452353602875…
Estos números decimales que no son periódicos ni exactos son los números irracionales (I), los números decimales exactos y periódicos, forman el conjunto de los números racionales (Q). Los números reales (R) están formados por los racionales y los irracionales.
SUMA Y RESTA DE NÚMEROS DECIMALES:
Como la suma habitual, alineando la coma y suponiendo o completando con ceros las posiciones inexistentes:
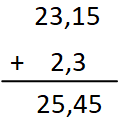
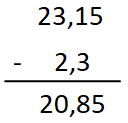
MULTIPLICACIÓN DE NÚMEROS DECIMALES:
Como la multiplicación habitual de números enteros, pero teniendo en cuenta de incluir la coma en el resultado, de tal manera que sea la suma de las posiciones decimales de los dos números:

Notar que en el resultado se ha incluido la coma para tener dos decimales, la suma de cada uno de los decimales de los números que multiplicamos.
APROXIMACIÓN DE NÚMEROS DECIMALES, POR REDONDEO O TRUNCAMIENTO:
Una vez definido el nivel de exactitud que deseamos podemos actuar por redondeo o truncamiento:
REDONDEO: Se tiene en cuenta la cifra inmediatamente a la derecha de la posición deseada; si esa cifra es mayor o igual que 5, se una 1 a la cifra de la posición que queremos redondear, si es menor que cinco se deja igual.
π = 3,1415926535897932384626433…
Deseamos redondear π a la milésima: π = 3,1415926535897932384626433…
Como la cifra inmediatamente a la derecha de la milésima es igual o mayor que 5, se añade una unidad a la milésima:
π = 3,142
Deseamos redondear π a la centésima: : π = 3,1415926535897932384626433…
Como la cifra inmediatamente a la derecha de la centésima es menor que 5, se deja igual la centésima:
π = 3,14
TRUNCAMIENTO: Se eliminan las cifras decimales que están después de la cifra que ocupa la posición deseada para aproximar:
π = 3,1415926535897932384626433…
Deseamos truncar π a la milésima: π = 3,1415926535897932384626433…
π = 3,141
Deseamos truncar π a la centésima: π = 3,1415926535897932384626433…
π = 3,14
