PROBLEMAS MCM Y MCD
PROBLEMAS DE MÍNIMO COMÚN MÚLTIPLO (MCM) Y DE MÁXIMO COMÚN DIVISOR (MCD). DIVISIBILIDAD):
PUEDE INTERESAR LA CONSULTA DEL SIGUIENTE ARTÍCULO RELACIONADO CON LA DIVISIBILIDAD:
SIGUE EL ESQUEMA DETERMINADO POR LA PROPUESTA DE PROGRAMACIÓN DE MATEMÁTICAS PARA 1º DE LA E.S.O.:
INDICACIONES QUE PUEDEN AYUDAR PARA DIFERENCIAR SI SE TRATA DE CALCULAR EL MÍNIMO COMÚN MÚLTIPLO O EL MÁXIMO COMÚN DIVISOR:
Suele ocurrir que la búsqueda del MCM para resolver el problema, ocurre en los casos en los que nos pregunten por algo que coincida o se encuentre si se repite en el tiempo, y super importante, tener en cuenta que la respuesta a la pregunta será un número mayor o incluso igual que los números que se nos dan en el problema.
Factores comunes y no comunes elevados al mayor exponente.
Para el MCD, podemos tener en cuenta que será la respuesta frecuentemente cuando haya que hacer grupos, dividir o repartir en partes iguales y suele estar en el enunciado palabras como «el máximo», «el mayor», «el más grande»…
Factores comunes elevados al menor exponente.
El mayor de los divisores comunes, es el número más grande que divide a dos o más números.
EJERCICIO M1EE3285:
Luis va a ver a su abuelo cada 6 días y su prima Noemí cada 4 días. Hoy han coincidido en casa de su abuelo. ¿Dentro de cuántos días volverán a verse en casa de su Abuelo?
SOLUCIÓN DEL EJERCICIO:
4 = 22 ; 6 = 2 · 3
M.C.M. = 22 · 3 = 12
Notar que en términos de factores, elegimos los comunes (2) y no comunes (3) elevados al mayor exponente con el que aparecen (22 · 3)
Volverán a coincidir, dentro de 12 días
Puede ayudar, el siguiente esquema:
Luis: 4 8 12 16 … (Luis irá dentro de 4 días, después 8 días, después 12 días….)
Noemí: 6 12 18 … (Noemí irá dentro de 6 días, después 12 días….)
EJERCICIO M1EE3286:
Disponemos de dos tiras de madera, una de 24 cm y la otra de 18 cm, con la que pretendemos hacer palitos para polos de hielo. ¿De qué medida tenemos que cortarlas para que los palitos que resulten sean iguales pero lo más largos posible?
SOLUCIÓN DEL EJERCICIO:
Descomponiendo en factores:
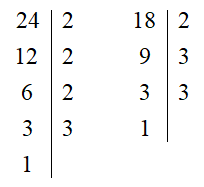
24 = 23 · 3 ; 18 = 2 · 32 ,
Se trata de un problema de MCD, donde se puede ver que los factores comunes elevados al menor exponente con el que aparecen, serían el 2 y el 3, ambos elevados a 1. Por ello:
M.C.D. (24, 18) = 2 · 3 = 6
Los palitos resultarán de 6 cm cada uno.
EJERCICIO M1EE3287:
En una salida complementaria de un instituto, a la que acuden 24 alumnos de 1º Bachillerato A y 36 alumnos de 1º Bachillerato B, se desea formar grupos con las siguientes condiciones:
- Todos los grupos deben tener el mismo número de alumnos.
- En los grupos formados sólo puede haber alumnos de la misma clase.
¿Cuál es el mayor número de alumnos que puede haber en cada grupo para que se cumplan esas condiciones? ¿Cuántos grupos se formarán en total?
SOLUCIÓN:
PRIMERA FORMA: Con los divisores
Necesitamos obtener el MCD que sabemos que es el divisor común más grande de dos números.
Divisores de 24: 1, 2, 3, 4, 6, 8, 12, 24
Divisores de 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
MCD (24, 36) = 12
SEGUNDA FORMA: Descomponiendo en factores

24 = 23 · 3 ; 36 = 22 · 32
Factores comunes y no comunes elevados al menor exponente: 22 · 3
MCD (24, 36) = 22 · 3 = 12
Se formarán grupos de 12 alumnos, correspondiendo 2 grupos a 1º A y 3 grupos a 1º B, 5 grupos en total.
EJERCICIO M1EE3288:
En Las Palmas, dos líneas de guaguas pasan por una misma parada. La primera guagua pasa cada 15 minutos y la segunda pasa cada 20 minutos. Si ambos pasan por la parada a las 8:00 AM, ¿a qué hora se encontrarán nuevamente en la parada después de las 8:00 AM?
MCM (15, 20) = 60
EJERCICIO M1EE3289:
El Carrizal de Tejeda tiene dos servicios de recogida de basura. El primer servicio pasa cada 12 días y el segundo cada 18 días. Si ambos servicios recogen basura el mismo día, ¿cuántos días pasarán hasta que vuelvan a coincidir?
MCM (12, 18) = 36
EJERCICIO M1EE3290:
En una oficina, dos equipos tienen reuniones periódicas. El primer equipo se reúne cada 8 días y el segundo cada 14 días. Si ambos equipos tienen reuniones el mismo día, ¿cuántos días deberán esperar hasta que sus reuniones coincidan de nuevo?
MCM (8, 14) = 56
EJERCICIO M1EE3291:
En una iglesia, dos campanas suenan al mediodía. La primera suena cada 25 minutos y la segunda cada 30 minutos. Si ambas suenan juntas al mediodía, ¿cuánto tiempo pasará hasta que suenen juntas de nuevo?
MCM (25, 30) = 150
EJERCICIO M1EE3292:
Una fábrica produce dos tipos de productos. El primer tipo de producto se fabrica cada 40 minutos, y el segundo tipo cada 60 minutos. Si ambos tipos se fabrican al mismo tiempo en un turno, ¿después de cuánto tiempo volverán a fabricarse simultáneamente?
MCM (40, 60) = 120
EJERCICIO M1EE3293:
Se tienen dos cuerdas de 84 cm y 210 cm. Queremos cortarlas en trozos iguales, lo más largos posible, sin que sobre nada. ¿Cuánto mide cada trozo?
MCD (84, 210) = 42
EJERCICIO M1EE3294:
Un agricultor tiene un terreno rectangular de 96 m de largo y 72 m de ancho. Quiere dividirlo en parcelas cuadradas lo más grandes posible. ¿Cuánto mide el lado de cada parcela y cuántas parcelas obtiene?
MCD (96, 72) = 24
EJERCICIO M1EE3295:
Un colegio tiene 45 alumnos de primaria y 60 alumnos de secundaria. Se quieren organizar excursiones usando grupos de igual tamaño y sin mezclar niveles. ¿Cuántos alumnos como máximo puede tener cada grupo?
MCD (45, 60) = 15


