REGLA RUFFINI DIVISIÓN POLINOMIOS
REGLA DE RUFFINI PARA DIVISIÓN DE POLINOMIOS:
PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- DESCOMPOSICIÓN FACTORIAL DE POLINOMIOS
- REGLA DE RUFFINI PARA FACTORIZAR (DESCOMPONER) POLINOMIOS
- ECUACIONES DE PRIMER GRADO
- ECUACIONES DE PRIMER Y SEGUNDO GRADO. MATEMÁTICAS SECUNDARIA
- ECUACIONES PARA SECUNDARIA. ÁLGEBRA
- ECUACIONES PELIGROSAS PARA MATEMÁTICAS DE SECUNDARIA Y BACHILLERATO
- MATERIALES DE ÁLGEBRA PARA 1º DE BACHILLERATO. ECUACIONES
- ECUACIONES DE GRADO SUPERIOR A DOS, PARA SECUNDARIA
SIGUE EL ESQUEMA DETERMINADO POR LA PROPUESTA DE PROGRAMACIÓN DE MATEMÁTICAS PARA 4º DE LA E.S.O.: MATEMÁTICAS DE 4º DE LA E.S.O.. DESARROLLO DE LA ASIGNATURA
REGLA DE RUFFINI Y SU USO PARA DIVIDIR POLINOMIOS:
Esta regla es una forma de dividir polinomios de grado cualquiera entre polinomios de la forma (x – a), de primer grado.
El primer ejemplo con el que vamos a trabajar corresponde a dividir el polinomio (x2 + 2x + 1) entre (x + 1) [notar como a=-1]
Con Ruffini, se trazan dos líneas rectas, una horizontal y otra vertical, a modo de cruz, que nos ayudarán a poner orden en los números.
Se trata de colocar los coeficientes del polinomio ordenado en la primera fila horizontal (si algún término no existe, se pone un cero en su posición), a la derecha de la línea vertical. (esto en nuestro caso es «1 0 1»)
El valor de a (en nuestro caso a = – 1)se coloca en el extremo izquierdo (a la izquierda de la línea vertical en la segunda fila).
El primer número (coeficiente del término de mayor grado) de esta serie se baja directamente a la tercera fila horizontal, debajo de la línea recta horizontal (proceso que se indica en el ejemplo mediante la flecha negra),
El número en el extremo izquierdo [el número «a» de (x – a); -1 en nuestro caso] se multiplica por este primer número que hemos bajado a la tercera línea y el resultado de esta multiplicación se coloca en la segunda línea horizontal debajo del siguiente número (proceso indicado mediante las flechas azules) y se suman (el de la primera fila con el de la segunda). Se repite el proceso con este número (flechas rojas). El último de los números obtenidos es el resto (cero en nuestro caso- división exacta-).
La tercera fila es el cociente de la división (x+1), que tiene un grado menos que el dividendo (x2+2x+1).
El último de los números obtenidos es el resto (cero en este primer ejemplo – división exacta-).

Al final del proceso; la división de (x2 + 2x + 1) entre (x + 1) da como cociente (x + 1) y resto cero, tal y como hubiera ocurrido si hacemos la división clásica que se muestra:
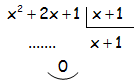
EJERCICIO M3EE3259:
Dividir el polinomio P(x) = x3 – 7x2 + 8x + 16 entre Q(x) = x – 4
RESOLUCIÓN:

Notar los procesos indicados por las flechas tal y como se hizo en el primer ejemplo, con lo que:
el cociente es C(x) = x2 – 3x – 4 ; y el resto es R(x) = -1.
