DESCOMPOSICIÓN FACTORIAL DE POLINOMIOS:
PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- REGLA DE RUFFINI PARA DIVISIÓN DE POLINOMIOS
- REGLA DE RUFFINI PARA FACTORIZAR (DESCOMPONER) POLINOMIOS
- ECUACIONES DE PRIMER GRADO
- ECUACIONES DE PRIMER Y SEGUNDO GRADO. MATEMÁTICAS SECUNDARIA
- ECUACIONES PARA SECUNDARIA. ÁLGEBRA
- ECUACIONES PELIGROSAS PARA MATEMÁTICAS DE SECUNDARIA Y BACHILLERATO
- MATERIALES DE ÁLGEBRA PARA 1º DE BACHILLERATO. ECUACIONES
- ECUACIONES DE GRADO SUPERIOR A DOS, PARA SECUNDARIA
SIGUE EL ESQUEMA DETERMINADO POR LA PROPUESTA DE PROGRAMACIÓN DE MATEMÁTICAS PARA 4º DE LA E.S.O.: MATEMÁTICAS DE 4º DE LA E.S.O.. DESARROLLO DE LA ASIGNATURA
PARA DESCOMPONER EN FACTORES UN POLINOMIO EXISTEN LAS SIGUIENTES ESTRATEGIAS:
Descomponer en factores es expresar el polinomio como producto de factores primos.
- Sacar factor común
- Utilizar los productos notables, a la inversa
- Resolver la ecuación de segundo grado, correspondiente al polinomio de segundo grado en su caso.
- Utilizar Ruffini
Con estas estrategias, podemos simplificar fracciones algebraicas, resolver ecuaciones…
OBTENER, SACAR FACTOR COMÚN EN UN POLINOMIO:
Sacar factor común en un polinomio, es expresar el polinomio de forma que lo que está repetido en todos los términos del polinomio, aparezca sólo una vez y multiplicando al resto del polinomio.
EJEMPLO M2EE3255:
x2 + 3x = x · (x + 3 )
Notar como la “x” aparece en los dos términos del polinomio, con lo que este término repetido sólo lo ponemos una vez, es el FACTOR COMÚN, que lo expresamos multiplicando al resto.
EJEMPLO M2EE3256:
3x2 + 6x + 9 = 3·x2 + 3·2x + 3·3 = 3 · (x2 + 2x +3)
Notar como el “3” aparece en todos los términos del polinomio, con lo que es el FACTOR COMÚN y podemos ponerlo sólo una vez y multiplicando a lo demás.
EJEMPLO M2EE3257:
5x2 + 10x = 5x·x +5x·2 = 5x · (x+2)
Caer en la cuenta como en los dos términos, en «5x2» y «10x» tenemos incluido el factor 5x, que es el FACTOR COMÚN, que aparece repetido en todos los términos del binomio, con lo que podemos expresarlo como el producto de ese factor repetido y «lo que le falta» a cada uno de ellos entre paréntesis. Si comprobamos al revés vemos que efectivamente:
5x·(x+2) = 5x2 + 10x; coincide con lo que teníamos al principio.
En todos los casos en los que extraemos factor común es muy interesante realizar la multiplicación con posterioridad a extraer factor común: esta comprobación, para ver que realmente no nos hemos equivocado y la expresión utilizando el factor común coincide con lo que teníamos al principio.
Esto de sacar factor común es conveniente cuando nos encontramos con fracciones algebraicas, para poder simplificarlas, ya que para poder simplificar, el término a simplificar tiene que estar arriba (Numerador) y abajo (Denominador) y además en los dos casos, multiplicando a todo lo demás:
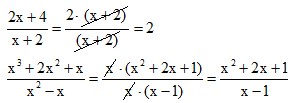
LOS PRODUCTOS NOTABLES PARA DESCOMPONER POLINOMIOS DE SEGUNDO GRADO:
Los productos notables, las identidades notables básicas:
(a + b)2 = a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2
(a + b) · (a – b) = a2 – b2
sirven para desarrollar binomios, aplicando la fórmula directamente.
Si vemos las fórmulas, IDENTIDADES NOTABLES, a la inversa:
a2 + 2ab + b2 = (a + b)2
a2 – 2ab + b2 = (a – b)2
a2 – b2 = (a + b) · (a – b)
Las podemos utilizar para DESCOMPONER POLINOMIOS DE SEGUNDO GRADO, en los que vemos el producto notable del que procede (no siempre es fácil).
EJEMPLOS de este tipo de DESCOMPOSICIÓN DE POLINOMIOS DE SEGUNDO GRADO:
x2+2x+1, se vé muy claro que corresponde a (x+1)2
Sin embargo, 4x2+4x+1, podría no verse tan claro que corresponde a (2x+1)2
o incluso, 9x2+12x+4, podría ser igual de complicado ver que es (3x+2)2
si tenemos, 9x2-12x+4, comprobar que es (3x-2)2
Con lo que cuando no se tiene muy claro, lo mejor es recurrir a RESOLVER LA ECUACIÓN DE SEGUNDO GRADO para descomponerlo, que puede que tardemos menos.
ECUACIÓN DE SEGUNDO GRADO:
La ecuación de segundo grado es la que la incógnita aparece elevada a dos. Para resolverla hay que ordenarla de mayor a menor grado y que quede igual a cero, de la forma:
ax2 + bx + c = 0
donde «a» es lo que acompaña a x2; «b» lo que acompaña a x; «c» el término independiente (lo que está suelto)
Una vez hecho esto, se resuelve con la fórmula general:
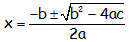
EJEMPLO M2EE3258:
Descomponer en factores el polinomio: P(x) = x2 – 5x + 6
RESOLUCIÓN:
Primero, resolver la ecuación: x2 – 5x + 6 = 0
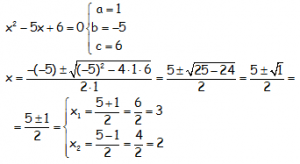
Aparte de que estos valores: x = 3; x = 2, son las soluciones de la ecuación, esto nos permite descomponer el factores el polinomio P(x) = x2 – 5x + 6, ya que cuando resolvemos una ecuación cualquiera del tipo:
Polinomio=0, este polinomio se puede expresar como:
(x – solución1) · (x – solución2) · ….. · (x – soluciónn)
que nos permite además descomponer el polinomio en factores.
Por ello el polinomio P(x) = x2 – 5x + 6, del que ya conocemos las soluciones, se puede expresar como:
P(x) = x2 – 5x + 6 = (x-3) · (x-2)
UTILIZANDO LA REGLA DE RUFFINI:
IR AL ARTÍCULO QUE LO DOCUMENTA: REGLA DE RUFFINI PARA FACTORIZAR (DESCOMPONER) POLINOMIOS
Con todo lo anterior, resolver el siguiente ejercicio:
EJERCICIO M3EE1893:
Simplificar las siguientes fracciones algebraicas:
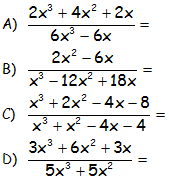
IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: EJERCICIO M3EE1893 RESUELTO DE SIMPLIFICACIÓN DE FRACCIONES ALGEBRAICAS
