EXAMEN BLOQUE ANÁLISIS FUNCIONES
EXAMEN RESUELTO BLOQUE DE ANÁLISIS DE FUNCIONES, PARA MATEMÁTICAS II DE 2º BACHILLERATO. PRUEBA 3 DEL PRIMER TRIMESTRE CURSO 2025-26, REALIZADO EN «EL PILAR»:
PUEDE INTERESAR LA CONSULTA DE:
-
- EJERCICIOS DE ANÁLISIS DE FUNCIONES. MATEMÁTICAS 2º BACHILLERATO
- FUNCIONES: ANÁLISIS PARA BACHILLERATO
- ESTUDIO DE LA DERIVABILIDAD DE UNA FUNCIÓN
- LÍMITES: USO DEL NÚMERO «e» PARA RESOLVER INDETERMINACIONES
- REGLA DE L’HÔPITAL PARA EL CÁLCULO DE LÍMITES. MATEMÁTICAS BACHILLERATO
- APLICACIONES DE LA DERIVADA. OPTIMIZACIÓN Y CÁLCULO DE PARÁMETROS.
- INTEGRALES Y DERIVADAS. PROBLEMAS CONTEXTUALIZADOS
- LA DERIVADA ES VARIACIÓN Y LA INTEGRAL ES SU OPERACIÓN INVERSA
- CÁLCULO DE INTEGRALES PARA MATEMÁTICAS DE BACHILLERATO
ESTA PRUEBA SIGUE LA DINÁMICA QUE SE REFLEJA EN LA PROGRAMACIÓN PARA ESTE CURSO DE MATEMÁTICAS II DE 2º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA: MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
LOS ENUNCIADOS DE LA PRUEBA, DE ANÁLISIS DE FUNCIONES (X1082):
X1083 MATEMÁTICAS II 2 BAC ANÁLISIS. PRUEBA 3 TRIM 1 2526LOS EJERCICIOS DE LA PRUEBA Y SU RESOLUCIÓN:
EJERCICIO M2BE3382:
Resolver la siguiente integral indefinida:
RESOLUCIÓN PASO A PASO DE LA INTEGRAL:
EJERCICIO M2BE3382 INTEGRAL DIVISIÓN ARCOTANGENTE_V1
EJERCICIO M2BE3383:
Resolver la siguiente integral indefinida:
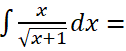
RESOLUCIÓN PASO A PASO DE LA INTEGRAL:
EJERCICIO M2BE3383 INTEGRAL SUSTITUCIÓN_V1
EJERCICIO M2BE3384:
Resolver la siguiente integral indefinida:
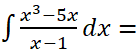
RESOLUCIÓN PASO A PASO DE LA INTEGRAL:
EJERCICIO M2BE3384 INTEGRAL DIVISIÓN LOGARITMO NEPERIANO_V1
EJERCICIO M2BE3385:
Resolver la siguiente integral indefinida:
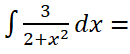
RESOLUCIÓN PASO A PASO DE LA INTEGRAL:
EJERCICIO M2BE3385 INTEGRAL ARCOTANGENTE_V1
EJERCICIO M2BE3386:
Para la siguiente función f(x):
Calcular el dominio y los extremos relativos.
RESOLUCIÓN DEL EJERCICIO:
Ejercicio M2BE3386 DOMINIO Y EXTREMOS EXPONENCIAL_V1
EJERCICIO M2BE3387:
Para la siguiente función f(x):
Calcula la recta tangente en x = 1 .
RESOLUCIÓN DEL EJERCICIO:
Ejercicio M2BE3387 recta tangente función exponencial_V1
EJERCICIO M2BE3388:
Dada la siguiente función f(x), hallar los valores de a y b, para que sea derivable en todo ℜ.
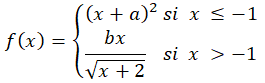
Donde a y b pertenecen a ℜ.
RESOLUCIÓN DEL EJERCICIO:
EJERCICIO M2BE3388 ESTUDIO DE DERIVABILIDAD FUNCIÓN A TROZOS_V1
EJERCICIO M2BE2442:
Hallar la función polinómica 𝑓(𝑥) que verifica que tiene un punto mínimo en 𝑀(2,-10) y su segunda derivada es: f’’(x) = x + 4 . Dar la expresión de 𝑓(𝑥).
RESOLUCIÓN PASO A PASO DEL EJERCICIO:
EJERCICIO M2BE2442 INTEGRALES Y DERIVADAS_v1