ASÍNTOTAS VERTICALES HORIZONTALES OBLÍCUAS
ASÍNTOTAS VERTICALES, HORIZONTALES Y OBLÍCUAS. RAMAS PARABÓLICAS: APLICACIONES DE LOS LÍMITES DE FUNCIONES:

PUEDE INTERESAR LA CONSULTA DE:
-
- FUNCIONES: ANÁLISIS PARA 1º BACHILLERATO. EJERCICIOS
- ANÁLISIS DE FUNCIONES PARA 2º BACHILLERATO. EJERCICIOS
- PROPIEDADES DE LOS LÍMITES DE FUNCIONES
- LÍMITES PARA MATEMÁTICAS DE BACHILLERATO
- LÍMITES: USO DEL NÚMERO «e» PARA RESOLVER INDETERMINACIONESREGLA DE L’HÔPITAL PARA EL CÁLCULO DE LÍMITES. MATEMÁTICAS BACHILLERATO
SIGUE LA DINÁMICA QUE SE REFLEJA EN LA PROGRAMACIÓN PARA ESTE CURSO DE MATEMÁTICAS II DE 2º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA:
ASÍNTOTAS. APLICACIONES DE LOS LÍMITES:
ASÍNTOTAS VERTICALES:
La condición de presencia de una asíntota vertical en una función f(x) :

Haremos este límite, y si el resultado es infinito, la función presenta una asíntota vertical de ecuación x = a .
Los posibles valores de a en los que debemos plantearnos la posibilidad de Asíntota Vertical son:
-
- Los valores que anulen el denominador en las funciones racionales, igualando el denominador a cero.
- Cuando tenemos funciones logarítmicas, del tipo log [f (x)] , aquellos valores en los que f(x)=0 , ya que el logaritmo de cero tiende a -∞
- Cuando tenemos funciones trigonométricas con la tangente, del tipo tg [f (x)] , aquellos valores en los que f(x) = π/2 + kπ. Tengamos en cuenta que la tangente de 90º y 270º son +∞ y -∞ respectivamente.
El estudio completo consiste en calcular los límites por la derecha e izquierda del punto a, y fijarse en el signo del infinito que resulta, de tal manera que ésa será la tendencia a ambos lados de la asíntota vertical, lo cual además aporta muchísima información a la hora de representar la función.
ASÍNTOTAS HORIZONTALES:
![]()
El estudio completo consiste en calcular el límite cuando x tiende a infinito y a menos infinito, ya que la asíntota puede ser diferente a cada lado e incluso no tener en uno de ellos. Esto último es sobre todo interesante en funciones con radicales, exponenciales y otras complicadas.
Además se suele calcular la POSICIÓN DE LA CURVA CON RESPECTO A LA ASÍNTOTA, dato que se obtiene calculando el signo de la diferencia entre la función y la asíntota, teniendo en cuenta que es un razonamiento para valores grandes de la variable con el signo que corresponda.
Si el signo de [f(x) – k] es positivo, es la curva la que está por encima de la asíntota, y si es negativo es la asíntota la que está por encima.
*Si la función tiene asíntota horizontal, no se realiza el cálculo de la oblícua, porque al ser la asíntota horizontal un caso particular de asíntota oblícua, daría lo mismo. (Esta cuestión se aclara con detalle a continuación de la exposición de ramas parabólicas)
ASÍNTOTAS OBLICUAS:
f(x) presenta una asíntota oblicua de ecuación y = mx + n si tanto m como n tienen sentido (dan números finitos) calculados de la siguiente forma:
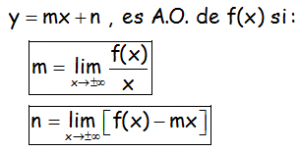
Se puede dar el caso, al igual que con las asíntotas horizontales, que sean diferentes las asíntotas oblicuas hacia la derecha y hacia la izquierda, por lo que hay que calcular estos límites cuando x tiende a infinito y cuando x tiende a menos infinito.
El estudio completo también requiere el conocimiento de la posición de la curva con respecto a la asíntota que se sabe calculando el signo de [f(x) – (mx+n)] para valores grandes de x positivos y negativos (sustituyendo por ejemplo por x=1000 ó x=-1000); si da positivo, la función está por encima de la asíntota, si negativo, la función está por debajo.
RAMAS PARABÓLICAS O INFINITAS:
En el cálculo de las asíntotas oblicuas, m puede presentar diferentes casos:
-
- Si m es un número real no nulo, la función tiene una asíntota oblícua en +∞ ó -∞ según el caso.
- Si m=±∞ , la función no tiene asíntota oblicua en +∞ ó -∞ según el caso, sino que presenta una rama parabólica con forma de parábola vertical y=x2. (RAMA PARABÓLICA SEGÚN EJE OY)
- Si m=0, presenta una RAMA PARABÓLICA SEGÚN EJE OX. (Forma de parábola horizontal del tipo y=√x )
SI UNA FUNCIÓN TIENE ASÍNTOTA HORIZONTAL, «NO TIENE OBLÍCUA»:
Si una función presenta una asíntota horizontal, lo que ha ocurrido es que:
![]()
y la asíntota horizontal es de ecuación y = k.
Como para el cálculo de la asíntota oblícua y = mx + n , tenemos que calcular m y n, cuando lo hacemos resulta que nos darán los siguientes resultados, que se confirman con las propiedades de los límites:
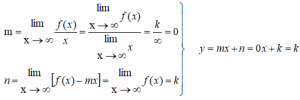
La asíntota oblicua coincide con la horizontal, al darnos m = 0 y n = k, sería «y = k» , con lo que es innecesario el cálculo de la oblícua.
EJERCICIOS DE INTERÉS, YA QUE SON ALGUNOS CASOS EN LOS QUE LAS ASÍNTOTAS HORIZONTALES O LAS OBLÍCUAS SON DIFERENTES CUANDO x → +∞ Ó CUANDO x → -∞ :
EJERCICIO M2BE3478:
Hallar las asíntotas de la siguiente función:
![]()
EJERCICIO M2BE3479:
Hallar las asíntotas de la siguiente función:
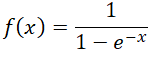
EJERCICIO M2BE3480:
Hallar las asíntotas de la siguiente función:
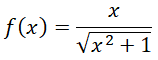
EJERCICIOS M1BE2178:
Realizar el estudio completo de las asíntotas de las siguientes funciones, realizando un boceto de las mismas utilizando la información obtenida e incluso alguna otra que se considere relevante (corte con los ejes, dominio…). Contrastar lo obtenido analíticamente con la representación gráfica, utilizando geogebra:
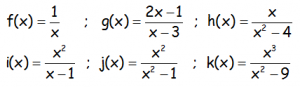
EJERCICIO M1BE2217:
Teniendo en cuenta la siguiente función:
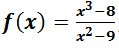
Obtener:
a.- Asíntotas.
b.- Cortes con los ejes.
IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO
EJERCICIO M1BE2472:
Calcular las asíntotas de la siguiente función, argumentando matemáticamente todo el proceso que se realiza:
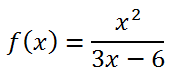
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN RESUELTO DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO. PRUEBA 1 DEL TERCER TRIMESTRE DEL CURSO 23-24.
EJERCICIO M1BE3068:
Para la siguiente función:

a.- Indicar su dominio.
b.- Cortes con los ejes.
c.- Asíntotas.
d.- Representar de manera aproximada la función con la información obtenida en los apartados anteriores.
IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN DE ANÁLISIS DE FUNCIONES RESUELTO, PARA MATEMÁTICAS I DE 1º BACHILLERATO. PRUEBA 3 DEL SEGUNDO TRIMESTRE DEL CURSO 2024-25
EJERCICIO M1BE3125:
Calcular las asíntotas de la siguiente función, argumenta matemáticamente todo el proceso que realizas. Tranquilo/a, tú sabes hacerlo.

IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN RESUELTO DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA. PRUEBA 1 DEL TERCER TRIMESTRE DEL CURSO 2024-25
EJERCICIO M2BE3473:
Calcula todas las asíntotas de la función f: ℜ → ℜ:
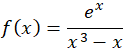
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO BLOQUE DE ANÁLISIS DE FUNCIONES Y ÁLGEBRA (MATRICES Y DETERMINANTES), PARA MATEMÁTICAS II DE 2º BACHILLERATO. PRUEBA 1 DEL SEGUNDO TRIMESTRE CURSO 2025-26, REALIZADO EN «EL PILAR»
EJERCICIO M2BE3060:
Considera la función f: ℜ→ℜ definida por f(x) = (x – 1) · e x .
a) Determina la ecuación de la recta tangente a la función f(x) en el punto de inflexión.
b) Estudia y calcula las asíntotas de la función. (Tener en cuenta en estos cálculos la opción en la que x tiende a menos infinito).
EJERCICIO M2BE2002 JL:
Realizar el estudio de las asíntotas horizontales de la siguiente función:
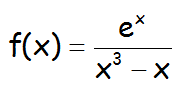
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/mfTP_-Sgen0
