MATEMÁTICAS FÍSICA QUÍMICA BACHILLERATO

ALGEBRA APLICADA ECUACIONES SISTEMAS

ÁLGEBRA APLICADA: MATEMÁTICAS Vs FÍSICA Y QUÍMICA DE BACHILLERATO:ALGEBRA APLICADA FISICA QUIMICA

Pretendemos con estas actividades que las matemáticas no sean un inconveniente para nuestros alumnos de bachillerato. Que ningún alumno fastidie su asignatura de Física y Química por culpa de no resolver bien ecuaciones e incluso sistemas de ecuaciones. Debemos ser conscientes que el uso en física de incógnitas diferentes de la «x» supone una dificultad añadida. De ahí el interés de este tipo de actividades en Matemáticas.

ASPECTOS FORMALES:

CON RESPECTO A LAS COMPETENCIAS CLAVE Y DESCRIPTORES OPERATIVOS ASOCIADOS:

CON RESPECTO A LOS SABERES BÁSICOS DE FÍSICA Y QUÍMICA DE 1º BACHILLERATO PREDOMINANTES EN LA ACTIVIDAD:

CON RESPECTO A LAS COMPETENCIAS ESPECÍFICAS DE FÍSICA Y QUÍMICA DE 1º DE BACHILLERATO QUE SE CONSIDERAN:

FYQ 1BAC C1 , FYQ 1BAC C2 , FYQ 1BAC C3 , FYQ 1BAC C4 , FYQ 1BAC C5 , FYQ 1BAC C6

CON RESPECTO A LOS CRITERIOS DE EVALUACIÓN, VINCULADOS A LAS CORRESPONDIENTES COMPETENCIAS ESPECÍFICAS:

FYQ1BAC1.1 , FYQ1BAC1.2 , FYQ1BAC2.3 , FYQ1BAC3.1 , FYQ1BAC3.3 , FYQ1BAC6.1 

Incluyen los descriptores operativos asociados

CON RESPECTO A LOS SABERES BÁSICOS DE MATEMÁTICAS DE 1º BACHILLERATO PREDOMINANTES EN LA ACTIVIDAD:

CON RESPECTO A LAS COMPETENCIAS ESPECÍFICAS DE MATEMÁTICAS DE 1º DE BACHILLERATO QUE SE CONSIDERAN:

MAT BAC C1 , MAT BAC C2 , MAT BAC C3 , MAT BAC C4 , MAT BAC C5 , MAT BAC C6 , MAT BAC C7 , MAT BAC C8 ,  MAT BAC C9 

CON RESPECTO A LOS CRITERIOS DE EVALUACIÓN DE MATEMÁTICAS I DE 1º DE BACHILLERATO

MATI1BAC1.1 , MATI1BAC1.2 , MATI1BAC2.1 , MATI1BAC2.2 , MATI1BAC3.1 , MATI1BAC4.1 , MATI1BAC5.1 , MATI1BAC5.2 , MATI1BAC6.1 , MATI1BAC6.2 , MATI1BAC7.1 , MATI1BAC7.2 , MATI1BAC8.1 , MATI1BAC8.2 , MATI1BAC9.1 , MATI1BAC9.2 , MATI1BAC9.3 

HIPERVINCULADOS A LOS DESCRIPTORES OPERATIVOS DE LAS COMPETENCIAS CLAVE

ESTE MATERIAL TIENE RELACIÓN CON ASPECTOS DEL PERFIL DE SALIDA DEL ALUMNADO DE LOS INSTITUTOS DIOCESANOS DE CANARIAS

EJERCICIO FYQ4EE2287: 

Hallar el valor de la F, en la siguiente ecuación, donde se considera que: μ=0,2; m=3,8 kg; v=cte; g=9,8 m/s2.

〈  F – μ·m·g = m·a 〉

EJERCICIO FYQ4EE2288: 

Hallar el valor de la aceleración, en la siguiente ecuación, donde se considera que: μ=0,2; m=3,8 kg; g=9,8 m/s2; F=13 N.

〈  F – μ·m·g = m·a 〉

EJERCICIO FYQ4EE2289: 

Hallar el valor de la aceleración, en la siguiente ecuación, donde se considera que: α=30º; μ=0,2; g=9,8 m/s2.

〈  – m·g·sen 30 – μ·m·g·cos 30 = m·a 〉

EJERCICIO FQ1BE2883:

Resolver la ecuación: «0 = 15 – 9,8 t» que representa el tiempo que tarda en alcanzar la altura máxima un objeto que se lanza desde el suelo con una velocidad de 15 m/s. En ella se considera g=9,8 m/s2.

EJERCICIO FQ1BE2884: (deriva de 1863)

Resolver la siguiente ecuación, que corresponde al tiempo que se tarda en llegar al alcance máximo en un movimiento parabólico concreto. Considerar g=9,8 m/s2. Tener en cuenta para el valor del seno, tener la calculadora en DEG.

Utilizar Geogebra para representar la parábola que nos indica la situación y comprobar los resultados obtenidos con ella.

EJERCICIO FQ1BE2885: (deriva de 1864)

Resolver la siguiente ecuación, que corresponde al tiempo que se tarda en llegar al alcance máximo en un movimiento parabólico concreto. Considerar g=9,8 m/s2.

Utilizar Geogebra para representar la parábola que nos indica la situación y comprobar los resultados obtenidos con ella.

EJERCICIO FQ1BE2886:

Resolver el sistema de ecuaciones formado por las dos ecuaciones siguientes:

〈 0,8 = V0·cos 60·t〉

〈 0,3 = 0,1 + V0·sen 60·t – 1/2 · 9,8·t2〉

Que corresponde al movimiento del salto de una rana.

EJERCICIO FQ4E2144:

Las ecuaciones que se muestran son el resultado de aplicar las características del movimiento vertical al MRUA, en el ejercicio que se enuncia:

“Se lanza una piedra verticalmente hacia arriba, alcanzando una altura de 35 m. Calcular la velocidad con que se lanzo y el tiempo que tarda en alcanzar la altura máxima. DATO: g =9,8 m/s2”

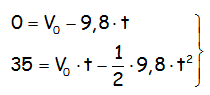
Resolver el sistema y por lo tanto obtener el valor de la velocidad inicial y del tiempo que tarda en alcanzar la altura máxima.

SOLUCIONES: 2,67 s; 26,166 m/s

EJERCICIO FQ1BE2160 r:

Las ecuaciones que se muestran son el resultado de aplicar las características del movimiento parabólico, en el ejercicio que se enuncia:

«Marta, extraordinaria jugadora de baloncesto, pretende encestar con un tiro libre. Ella sabe que la canasta está a 3,05 m de altura y que la distancia horizontal a la misma es de 4,06 m. Por su experiencia sabe que en el tiro libre la pelota sale de su mano con un ángulo de 60º y desde una altura de 1,85 m. Hallar la velocidad con que debe lanzar la pelota y el tiempo que tarda la misma en llegar a la canasta desde que sale de su mano. (DATO: g=9,8 m/s2)»

Resolver el sistema y por lo tanto obtener la velocidad inicial y el tiempo que se tarda en alcanzar la canasta.

SOLUCIONES: 7,8 m/s; 1,18 s

EJERCICIO FQ4EE2148:

Las ecuaciones que se muestran son el resultado de aplicar las Leyes de Newton a cuerpos enlazados, en el ejercicio que se muestra:

“ Dos cuerpos de masas 200 g y 400 g cuelgan a ambos lados de una polea, sin rozamiento y de masa despreciable. Hallar la aceleración del sistema, una vez se deja en libertad y la tensión de la cuerda.» 

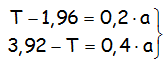
a.- Resolver el sistema y por lo tanto hallar lo que se solicita en el ejercicio.

b.- Utilizar Geogebra para representar las ecuaciones y encontrar y confirmar las soluciones a través de la representación gráfica.

EJERCICIO F2BE2290:

Hallar la velocidad de salida de los electrones en el efecto fotoeléctrico que resulta de aplicar la Ecuación de Einstein siguiente, donde: f=2·1015 Hz; h=6.63·10-34 J·s; f0=1.04·105 Hz: me=9.1·10-31 kg.

〈  h · f = h · f0 + 1/2 · me · v2 〉

EJERCICIO FQ1BE2368:

Resolver el siguiente sistema de ecuaciones, formado por las dos que se muestran, que corresponde a una situación de sistema de dos masas que se encuentra en un plano horizontal. Intentar obtener las características de la situación planteada.

T – 35,28 = 12 a

55,9 – T = 15 a

Post Views: 1.408
On:

Comments are closed, but trackbacks and pingbacks are open.