CRITERIOS DIVISIBILIDAD DESCOMPOSICIÓN FACTORES
CRITERIOS DE DIVISIBILIDAD. DESCOMPOSICIÓN EN FACTORES PRIMOS DE UN NÚMERO:
PUEDE INTERESAR LA CONSULTA DEL SIGUIENTE ARTÍCULO RELACIONADO CON LA DIVISIBILIDAD:
SIGUE EL ESQUEMA DETERMINADO POR LA PROPUESTA DE PROGRAMACIÓN DE MATEMÁTICAS PARA 1º DE LA ESO:
DESCOMPOSICIÓN EN FACTORES PRIMOS:
Cuando queremos descomponer un número en factores, podemos recurrir al sistema que se muestra, en el que empezamos por los números primos en orden: primero el 2, después 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, …
NÚMEROS PRIMOS DEL 1 AL 1000:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991 y 997…
Conocemos previamente si son divisibles entre 2, 3, 5, 7…. utilizando los criterios de divisibilidad:
CRITERIOS DE DIVISIBILIDAD:
Nos permiten conocer rápidamente si un número es divisible por otro. Si un número es divisible por otro, el resto de la división es cero.
Un número es divisible entre 2 si termina en cero o en cifra par.
Por ejemplo: 46, 58, 130, 26, …
Un número es divisible entre 3 si la suma de sus cifras es múltiplo de 3.
Por ejemplo: 9, 21, 63, 72, 276…
Un número es divisible entre 4 si sus dos últimas cifras son 00, o un múltiplo de 4.
Por ejemplo: 200, 400, 412, 84, 124…
Un número es divisible entre 5 si acaba en cero o en 5.
Por ejemplo: 15, 60, 245, 390….
Un número es divisible entre 6 si es divisible al mismo tiempo entre 2 y entre 3. Esto debe significar que termine en cero o cifra par, y al mismo tiempo la suma de sus cifras sea múltiplo de 3. Ejemplos: 36, 90, 126, …
Un número es divisible entre 9 si la suma de sus cifras da 9 o un múltiplo de 9.
Por ejemplo: 315, 54, 108, …
Un número es divisible entre 10 si termina en cero.
Por ejemplo: 20, 130, 1250, ….
Operativamente, lo que nos interesa a la hora de descomponer en factores un número, es ir descubriendo de menor a mayor, los factores primos entre los que es divisible. Empezamos planteándonos si es divisible entre 2, entre 3, entre 5, y seguimos.
Fijarse que en la división en cadena, se observa que las divisiones son exactas, con resto cero.
Por comodidad se utiliza el sistema de procesamiento en factores, con la línea vertical, dejando a la derecha los divisores. Este sistema nos permite ir más rápido, teniendo en cuenta que el resto de la división es cero, la división al pasar al siguiente escalón tiene que ser exacta:
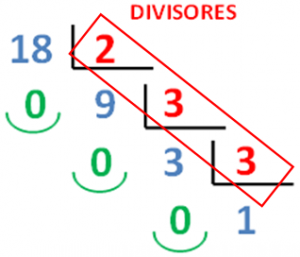
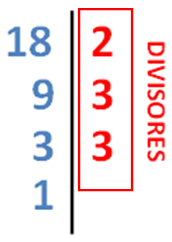
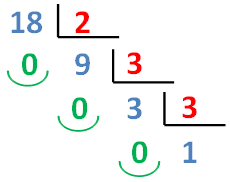
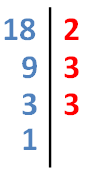
El objetivo es expresar el número que se descompone, en este caso el 18, del siguiente modo:
18 = 2 · 3 2
Se añaden los siguientes ejemplos:
EJERCICIOS / EJEMPLOS DE DESCOMPOSICIÓN EN FACTORES PRIMOS:
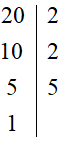20 = 2 2 · 5
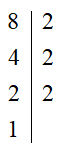8 = 2 3
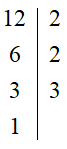12 = 2 2 · 3
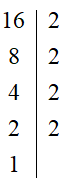16 = 2 4
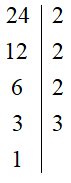24 = 2 3 · 3
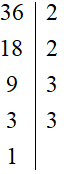36 = 2² · 3²
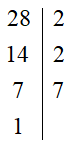28 = 2 2 · 7
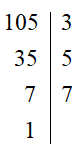105 = 3 · 5 · 7