EJERCICIO GRAVITACIÓN UNIVERSO PAU
EJERCICIO RESUELTO F2BE3199 DE GRAVITACIÓN EN EL UNIVERSO, PAU CANARIAS JUNIO 2025:

INTERESA LA CONSULTA DEL SIGUIENTE ARTÍCULO:
SIGUE LA DINÁMICA DETERMINADA POR:
EJERCICIO F2BE3199:
Demostrar que la energía total de un satélite que describe una órbita circular es igual a la mitad de su energía potencial.
RESOLUCIÓN DE ESTA CUESTIÓN TEÓRICA:
Al ser el campo gravitatorio un campo conservativo, la energía que tendrá el satélite en su órbita viene dada por la expresión de la energía mecánica (suma de las energías cinética y potencial).
![]()
Si ponemos el resultado de la VELOCIDAD ORBITAL, en la expresión de la energía cinética, puesto que el satélite está en órbita, obtenemos para la energía mecánica:
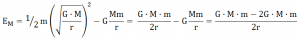
![]()
Que podemos notar que coincide con la mitad de la energía potencial, para un satélite que se mantiene en órbita.
