EJERCICIOS RESUELTOS ANÁLISIS CONTEXTUALIZADOS
EJERCICIOS DE ANÁLISIS DE FUNCIONES CONTEXTUALIZADOS PARA MATEMÁTICAS DE BACHILLERATO:
PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- TABLA DE DERIVADAS
- TASA DE VARIACIÓN MEDIA, INSTANTÁNEA, DERIVADA: DEFINICIÓN. EJERCICIOS RESUELTOS
- INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA DE UNA FUNCIÓN EN UN PUNTO
- ANÁLISIS DE FUNCIONES PARA BACHILLERATO
- INTEGRALES Y DERIVADAS. PROBLEMAS CONTEXTUALIZADOS
- ANÁLISIS EN PROFUNDIDAD DE UN MOVIMIENTO VARIADO COMO APLICACIÓN DE LAS DERIVADAS E INTEGRALES EN FÍSICA. PROBLEMAS CONTEXTUALIZADOS.
EJERCICIO M2BE3227 (PAU 2025 Convocatoria Extraordinaria-Julio Canarias):
El modelo logístico es un modelo matemático utilizado para describir la evolución de una población a lo largo del tiempo, cuando los recursos son limitados. Es uno de los modelos matemáticos más comunes en biología y describe cómo la población se estabiliza cuando alcanza la capacidad de carga del entorno, esto es, el tamaño máximo que puede alcanzar una población antes de que los recursos se vuelvan insuficientes, lo que genera competencia y, en muchos casos, una desaceleración de la tasa de crecimiento o una crisis en la población.
Un ejemplo de modelo logístico lo encontramos en las colonias de hormigas, que están compuestas por una red de túneles, entradas, cámaras de cría y áreas de almacenamiento, donde las hormigas establecen su hábitat.
Un grupo de investigadores ha estudiado el momento en el que unas hormigas forman una nueva colonia y ha modelizado el número de hormigas (H(t)) después de t meses con la función:
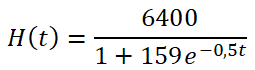
a) ¿Cuántas hormigas formaron la nueva colonia inicialmente?
b) ¿Cuál es la tasa media de crecimiento el primer año? ¿Y el segundo año? Interpretar el resultado.
PARA ESTE APARTADO PUEDE INTERESAR LA CONSULTA DEL SIGUIENTE ARTÍCULO: TASA DE VARIACIÓN MEDIA, INSTANTÁNEA, DERIVADA: DEFINICIÓN. EJERCICIOS RESUELTOS
c) Un observador afirma que el modelo siempre es creciente y entiende que la población de hormigas crece sin control. Justificar matemáticamente si esta afirmación es o no correcta.
d) ¿En qué momento la colonia de hormigas alcanzará la mitad de su capacidad de carga?
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO M2BE3227 DE ANÁLISIS DE FUNCIONES CONTEXTUALIZADO, PARA MATEMÁTICAS DE BACHILLERATO. PAU CANARIAS JULIO 2025
EJERCICIO M2BE3220 (PAU 2025 Convocatoria Ordinaria-Junio Canarias):
En un hospital de las Islas Canarias, un equipo de investigación está analizando cómo se metaboliza en sangre un nuevo medicamento llamado Metabolix, utilizado para tratar infecciones bacterianas. La concentración residual del fármaco en el plasma sanguíneo, denotada como f(x) (medida en miligramos por litro, mg/L), depende del tiempo transcurrido x (en horas) desde su administración. El estudio indica que el medicamento sigue dos fases diferenciadas:
- Fase de absorción: En las primeras dos horas, el fármaco se distribuye por el organismo.
- Fase de eliminación: A partir de la segunda hora, el fármaco empieza a eliminarse.
Este comportamiento se modeliza mediante la siguiente función matemática:
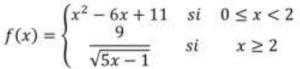
El equipo de investigación necesita aclarar algunas dudas del modelo matemático:
a) Confirmar si este modelo es realmente continuo. Justifica tu respuesta.
b) La concentración residual varía con el tiempo, comprobar que la velocidad de crecimiento instantánea de la concentración residual a las 3 horas de administrar Metabolix es mayor que -0.5 (mg/L)/h.
c) ¿Es cierto que la concentración residual del fármaco en la sangre siempre va disminuyendo con respecto al tiempo transcurrido? Averiguar en qué instante la concentración residual es máxima у calcular el valor de dicha concentración.
d) Pasado un largo periodo de tiempo, ¿cuál será la concentración residual de este medicamento?
IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE ANÁLISIS DE FUNCIONES CONTEXTUALIZADO: EJERCICIO M2BE3220 RESUELTO, CONTEXTUALIZADO DE ANÁLISIS. PAU CANARIAS JUNIO 2025
EJERCICIO M2BE3559:
La profundidad de la capa de arena en una playa se verá afectada por la construcción de un dique. En una zona de la playa, esa profundidad vendrá dada por la siguiente función:
Siendo P(t) la profundidad en metros y t el tiempo en años desde el inicio de la construcción. Si la profundidad llegara a superar los 4 metros, se debería elevar la altura del paseo marítimo.
a) ¿Es continua esta función? ¿Es siempre creciente? Justificar la respuesta.
b) ¿Cuál será la profundidad de la capa de arena al pasar 2 años desde el inicio de la construcción?
c) ¿Será necesario elevar la altura del paseo con el paso del tiempo, por causa de la profundidad de la arena? Justificar la respuesta.
IR A LA RESOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE MATEMÁTICAS II DE 2º DE BACHILLERATO CIENCIAS. TODOS LOS BLOQUES SEGÚN MODELO PAU CANARIAS. PRUEBA 1 DEL TERCER TRIMESTRE DEL CURSO 2025-26.
EJERCICIO M2BECCSS3475:
Durante los últimos 10 años, los costos en comunicaciones de una empresa, en decenas de miles de euros, vienen dados por la función:
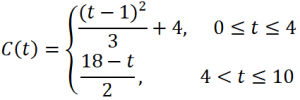
siendo 𝑡 el tiempo en años. Justificando la respuesta:
a) ¿Es continua 𝐶(𝑡)?
b) ¿Cuándo 𝐶(𝑡) es derivable? ¿Cuándo creció y cuándo decreció 𝐶(𝑡)?
c) ¿Cuándo alcanzó 𝐶(𝑡) el máximo y el mínimo absolutos? ¿Cuáles fueron los valores máximos y mínimos absolutos?
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE ANÁLISIS DE FUNCIONES Y PROBABILIDAD. MATEMÁTICAS 2º BACHILLERATO CIENCIAS SOCIALES. PRUEBA 1 DEL SEGUNDO TRIMESTRE DEL CURSO 2025-26, REALIZADO EN «EL PILAR»