INDETERMINACIÓN INFINITO MENOS INFINITO
INDETERMINACIÓN INFINITO MENOS INFINITO. LÍMITES PARA BACHILLERATO (∞-∞):

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- LÍMITES PARA MATEMÁTICAS DE BACHILLERATO
- REGLA DE L’HÔPITAL PARA EL CÁLCULO DE LÍMITES. MATEMÁTICAS BACHILLERATO
- INFINITÉSIMOS EQUIVALENTES PARA EL CÁLCULO DE LÍMITES (ampliación de contenidos)
- FUNCIONES: ANÁLISIS PARA 1º BACHILLERATO
- EJERCICIOS DE ANÁLISIS DE FUNCIONES
ESTÁ EN CONSONANCIA CON LAS ESTRATEGIAS DETERMINADAS POR LAS PROPUESTAS DE PROGRAMACIONES:
- MATEMÁTICAS I DE 1º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
- MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
- MATEMÁTICAS II APLICADAS A LAS CIENCIAS SOCIALES PARA 2º DE BACHILLERATO. DESARROLLO DE LA ASIGNATURA
INDETERMINACIÓN (∞-∞):
Se suele presentar en tres situaciones:
- Cuando calculamos límites de dos fracciones algebraicas que están restándose (o sumándose). En este caso, hacemos la operación (suma o resta) de las fracciones algebraicas.
- Cuando calculamos límites de la resta de dos expresiones con raíces. En este caso, multiplicamos y dividimos por el conjugado de la expresión con raíces.
- Cuando calculamos límites de la resta de dos infinitos y podemos utilizar la COMPARACIÓN DE INFINITOS
EJERCICIOS RESUELTOS DE CADA UNO DE LOS CASOS QUE SE PLANTEAN:
1.- Cuando calculamos límites de dos fracciones algebraicas que están restándose (o sumándose). En este caso, hacemos la operación (suma o resta) de las fracciones algebraicas.
EJERCICIO M2BE1832:
Hallar el siguiente límite:
RESOLUCIÓN DEL EJERCICIO:
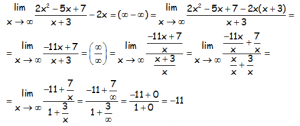
Notar como la indeterminación (∞-∞), se resuelve haciendo la operación (en este caso haciendo la resta -con el m.c.m.-) y posteriormente se transforma en otra indeterminación (∞/∞) hasta que se termina por resolver.
2.- Cuando calculamos límites de la resta de dos expresiones con raíces. En este caso, multiplicamos y dividimos por el conjugado de la expresión con raíces.
EJERCICIO M2BE82:
Hallar el siguiente límite:
RESOLUCIÓN DEL EJERCICIO:
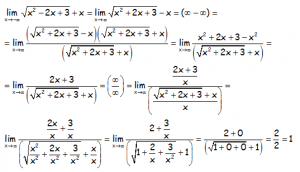
Hemos hecho el cambio de variable en el que cambiando la x por -x, podemos cambiar el -∞ por ∞, que seguramente mejora el razonamiento posterior.
Notar que hemos multiplicado y dividido por el conjugado.
3.- Cuando calculamos límites de la resta de dos infinitos y podemos utilizar la COMPARACIÓN DE INFINITOS
EJERCICIO M2BE1850; CASO DE INDETERMINACIÓN (∞/∞):
Calcular los siguientes límites:
RESOLUCIÓN DEL EJERCICIO:
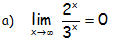
Ya que la exponencial del denominador es un infinito de orden superior al ser mayor la base.
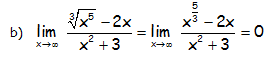
Ya que la potencial del denominador es un infinito de orden superior que la potencial del numerador.
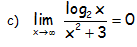
Ya que cualquier función potencial (polinómica) es un infinito de orden superior a cualquier logarítmica.
EJERCICIO M2BE1851; CASO DE INDETERMINACIÓN (∞-∞):
Calcular los siguientes límites:
RESOLUCIÓN DEL EJERCICIO:
![]()
Ya que el sustraendo es un infinito de orden superior al minuendo al ser mayor la base base.
![]()
Ya que la potencial del minuendo es un infinito de orden superior que la logarítmica del sustraendo.
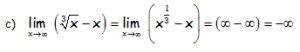
Ya que la función potencial (polinómica) del sustraendo es un infinito de orden superior a la del minuendo al tener mayor grado.
