SUSTITUCIÓN CAMBIO VARIABLE INTEGRALES
CÁLCULO DE INTEGRALES PARA MATEMÁTICAS DE BACHILLERATO
INTEGRALES POR SUSTITUCIÓN O CAMBIO DE VARIABLE PARA MATEMÁTICAS DE BACHILLERATO. EJEMPLOS:

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- CÁLCULO DE INTEGRALES PARA MATEMÁTICAS DE BACHILLERATO
- EJERCICIOS RESUELTOS DE INTEGRALES POR SUSTITUCIÓN O CAMBIO DE VARIABLE PARA MATEMÁTICAS DE 2º DE BACHILLERATO
- MÉTODO DE INTEGRACIÓN POR PARTES DE RESOLUCIÓN DE INTEGRALES PARA BACHILLERATO
SIGUE EL PROCESO DETERMINADO POR:
MÉTODO DE INTEGRACIÓN POR SUSTITUCIÓN O CAMBIO DE VARIABLE:
En ocasiones la integral que se nos propone, por causa de que la expresión del integrando aparece «en bloque», no la encontramos con facilidad en la TABLA DE INTEGRALES INMEDIATAS. Algunos de estos casos se pueden solucionar realizando un «cambio de variable». Hay quién acierta pensando en que hay que llamar «t» a lo que más molesta de la integral.
Para aplicar el método:
- Llamamos «t» al bloque. Hay quién acierta pensando en que hay que llamar «t» a lo que más molesta de la integral.
- Diferenciamos el cambio de variable, para poder cambiar el «dx» por el «dt» correspondiente (derivamos cada miembro de la expresión del cambio por separado y multiplicamos por el diferencial de la variable derivada).
- Se supone que con esto, si el método funciona bien, podemos resolver la integral si aparece en la TABLA DE INTEGRALES INMEDIATAS.
Lo más complicado es el punto 2, por lo que añadimos dos ejemplos de este punto:
Por ejemplo, si consideramos que el cambio adecuado es: t = 2x + 4, nos queda:
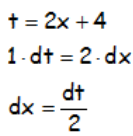
Notar como hemos derivado cada miembro por separado y despejamos dx para poder cambiarlo por su expresión en dt, para que en la integral haya coherencia entre la variable que integramos y el diferencial.
Si el cambio fuera:
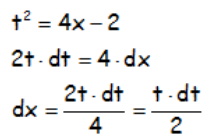
EN GENERAL EL MÉTODO FUNCIONA BIEN EN ESTOS TRES CASOS, de los que proponemos algunos EJEMPLOS (M2BP154):
A) Cuando la expresión del integrando “en bloque” hace que no nos aparezca en la tabla de inmediatas, llamar t al bloque nos puede resolver la integral).
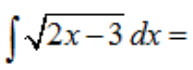
RESOLUCIÓN:
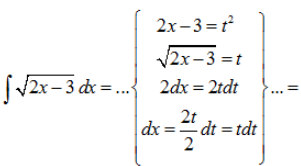
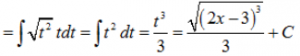
Se puede resolver también haciendo (2x-3=t) y transformando la raíz en exponente fraccionario, aunque es más recomendable según el ejemplo, intentarlo para ver que coincide la solución en los dos casos
B) Cuando en el cuerpo de la integral aparece una expresión y su derivada, el juego de llamar t a la expresión nos la simplifica y vemos la solución al transformarse en inmediata.
![]()
RESOLUCIÓN:
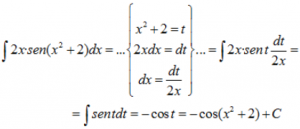
C) Un caso bastante más complicado: cuando tenemos que recurrir a la sustitución para transformar expresiones más complejas que aparecen en la integral.
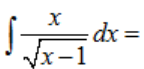
RESOLUCIÓN:
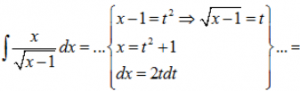
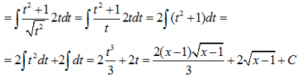
EJERCICIO M2BE2302:
Resolver las siguientes integrales indefinidas:
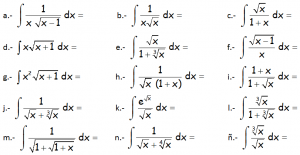
IR A LAS SOLUCIONES DE ESTAS INTEGRALES: EJERCICIOS RESUELTOS DE INTEGRALES POR SUSTITUCIÓN O CAMBIO DE VARIABLE PARA MATEMÁTICAS DE 2º DE BACHILLERATO
EJERCICIOS M2BE2074:
Resolver las siguientes integrales:
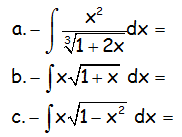
EJERCICIO M2BE3383:
Resolver la siguiente integral indefinida:
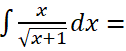
IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTA INTEGRAL: EXAMEN RESUELTO BLOQUE ANÁLISIS FUNCIONES. MATEMÁTICAS II DE 2º BACHILLERATO. PRUEBA 3 DEL PRIMER TRIMESTRE 2025-26.
EJERCICIO M2BE2613:
Realizar la siguiente integral indefinida,

IR A LA RESOLUCIÓN DETALLADA DE ESTA INTEGRAL: PRUEBA RESUELTA DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS II, DE 2º BACHILLERATO CIENCIAS. PRIMER TRIMESTRE 2024-25
EJERCICIOS M2BE3366:
Resolver las siguientes integrales, por el método más apropiado con el que consigas descubrir la “primitiva”:
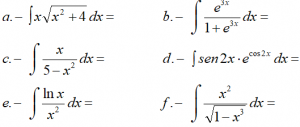
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EJERCICIOS RESUELTOS (M2BE3366) DE INTEGRALES PARA MATEMÁTICAS DE 2º DE BACHILLERATO. SUSTITUCIÓN, PARTES, INMEDIATAS
