REGLA RUFFINI FACTORIZAR POLINOMIOS
REGLA DE RUFFINI PARA FACTORIZAR (DESCOMPONER) POLINOMIOS:
PUEDE INTERESAR LA CONSULTA DE:
- DESCOMPOSICIÓN FACTORIAL DE POLINOMIOS
- REGLA DE RUFFINI PARA DIVISIÓN DE POLINOMIOS
- ECUACIONES DE PRIMER GRADO
- ECUACIONES DE PRIMER Y SEGUNDO GRADO. MATEMÁTICAS SECUNDARIA
- ECUACIONES PARA SECUNDARIA. ÁLGEBRA
- ECUACIONES PELIGROSAS PARA MATEMÁTICAS DE SECUNDARIA Y BACHILLERATO
- MATERIALES DE ÁLGEBRA PARA 1º DE BACHILLERATO. ECUACIONES
- ECUACIONES DE GRADO SUPERIOR A DOS, PARA SECUNDARIA
SIGUE EL ESQUEMA DETERMINADO POR LA PROPUESTA DE PROGRAMACIÓN DE MATEMÁTICAS PARA 4º DE LA E.S.O.: MATEMÁTICAS DE 4º DE LA E.S.O.. DESARROLLO DE LA ASIGNATURA
FACTORIZAR POLINOMIOS CON LA REGLA DE RUFFINI:
Se coloca el polinomio del mismo modo que se hace cuando se usa la regla de Ruffini para dividir polinomios (sólo los coeficientes del polinomio ordenados en la primera fila) y se trata de ir probando con sucesivos números hasta que nos dé el resto cero.
Estos números con los que probamos, son los divisores del término independiente del polinomio (con todas las posibilidades de signos).
El primer ejemplo con el que vamos a trabajar corresponde a descomponer en factores el polinomio P(x)=x2+2x+1
EJERCICIO M4EE3250:
Descomponer en factores el polinomio: P(x) = x2 + 2x + 1
RESOLUCIÓN DEL EJERCICIO:
Los divisores del término independiente con los que tenemos que ir probando son: +1, -1
Probando con +1:
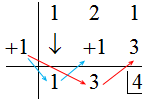
Notar como al darnos de resto +4, tenemos que seguir probando (+4 NO SIRVE).
Probando con -1:

Notar como en este caso, el resto nos da cero, indicándonos que efectivamente el x = – 1, es una raiz del polinomio. (Raíz de un polinomio es una solución de igualar el Polinomio a cero).
En este momento, nuestro polinomio se puede expresar como:
x2 + 2x + 1 = (x+1) · Cociente
Este factor (x+1) es el factor construido en plan (x-raíz) es por elllo por lo que es ( x-(-1) ) = (x+1)
El cociente, según Ruffini [VER RUFFINI DIVISION] corresponde a la última de las líneas, que tiene un grado menor que el polinomio del que partimos. es por ello por lo que el cociente es ( 1·x + 1 ), es decir (x+1)
Por ello el polinomio factorizado es; x2 + 2x + 1 = (x + 1) · (x + 1) = (x + 1)2.
Hemos partido de un ejemplo muy sencillo, que de hecho, se obtiene muy bien si nos fijamos que viene de un PRODUCTO NOTABLE.
EJERCICIO M4EE3251:
Factorizar el polinomio, P(x) = x3 + 3x2 – x – 3
RESOLUCIÓN DEL EJERCICIO:
Tendríamos que probar con los divisores de 3; esto es: +1,-1,+3,-3.
Comenzamos con el +1, para ver si es raíz del polinomio:

Notar como al darnos resto cero, el +1 es raíz del polinomio
En este momento, nuestro polinomio P(x) = x3 + 3x2 – x – 3 lo podemos expresar como:
P(x) = x3 + 3x2 – x – 3 = (x – 1) · Cociente = (x – 1) · (x2 + 4x + 3) , que aunque factorizado, no lo está del todo, ya que quizás se pueda seguir factorizando hasta grado 1 el cociente (x2 + 4x + 3).
Este cociente, para factorizarlo podemos incluso resolver la ecuación de segundo grado (x2+4x+3=0), y factorizarlo según (x – solución1) · (x – solución2), [que es lo que tendríamos que hacer si no le encontráramos soluciones por Ruffini], aunque vamos a seguir con Ruffini, para practicar esta regla:
Colocando de forma conveniente este polinomio: x2 + 4x + 3, y probando con -1:
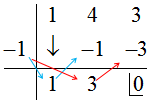
Al darnos resto = 0, confirmamos que el valor -1 es también raíz del polinomio, siendo (x+1) otro factor.
Con lo que en este momento, nuestro polinomio inicial:
P(x) = x3 + 3x2 – x – 3 = (x-1) · Cociente = (x – 1) · (x2 + 4x + 3) = (x- 1) · (x + 1) · (x + 3)
Ya que el cociente de esta operación final es (x+3), con lo que tenemos el polinomio factorizado totalmente.
