COMPARACIÓN INFINITOS CÁLCULO LÍMITES
COMPARACIÓN DE INFINITOS PARA EL CÁLCULO DE LÍMITES:
PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- INDETERMINACIÓN CERO DIVIDIDO ENTRE CERO. COCIENTE DE CEROS. LÍMITES
- LÍMITES: USO DEL NÚMERO «e» PARA RESOLVER INDETERMINACIONES
- REGLA DE L’HÔPITAL PARA EL CÁLCULO DE LÍMITES. MATEMÁTICAS BACHILLERATO
- INFINITÉSIMOS EQUIVALENTES PARA EL CÁLCULO DE LÍMITES (ampliación de contenidos)
- FUNCIONES: ANÁLISIS PARA 1º BACHILLERATO
- EJERCICIOS DE ANÁLISIS DE FUNCIONES
ESTÁ EN CONSONANCIA CON LAS ESTRATEGIAS DETERMINADAS POR LAS PROPUESTAS DE PROGRAMACIONES:
- MATEMÁTICAS I DE 1º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
- MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
- MATEMÁTICAS II APLICADAS A LAS CIENCIAS SOCIALES PARA 2º DE BACHILLERATO. DESARROLLO DE LA ASIGNATURA
La comparación de infinitos es una estrategia, un razonamiento que nos ayuda a resolver indeterminaciones sobre todo del tipo (∞/∞), pero también se puede utilizar en los casos (∞-∞).
Puede interesar ver previamente a la consulta del artículo, el siguiente video, de IDEA INTUITIVA DE LÍMITE, y de OBTENCIÓN DE LÍMITES POR COMPARACIÓN DE INFINITOS:
Decimos que f(x) es un infinito si:
![]()
Por ello:
![]()
Decimos que f(x) es un infinito de orden superior a g(x) si resulta que:
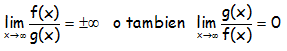
Recordemos que:
![]()
Siendo k un número cualquiera.
Lo anterior, aunque resulte un poco atrevido, se puede asimilar a:
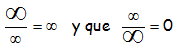
Lo que pretendemos hacer es conocer qué tipo de funciones tienden más rápidamente a infinito respecto de otras; las que tiendan más rápidamente a infinito serán infinitos de orden superior.
En la tabla, los valores correspondientes para una función exponencial: y=2x ; una función potencial: y=x2; y una logarítmica: y=log2x, para situarnos:
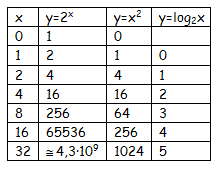
Se han tomado valores que sean sencillos de obtener.
Se observa muy bien como la exponencial crece más rápidamente que la potencial a su vez que la logarítmica, que crece muy despacio.
Por ello, es como si:
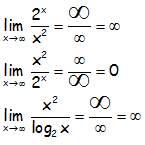
Que aunque no tiene mucho rigor (más bien ninguno) eso de infinitos más grandes y más pequeños, se entiende muy bien desde un punto de vista “operativo-didáctico”.
En conclusión y por lo anterior:
- Cualquier función exponencial de base mayor que uno es un infinito de orden superior a cualquier función potencial.
- Cualquier función potencial es un infinito de orden superior a cualquier función logarítmica.
Notar que los polinomios son funciones potenciales en las que se considera sólo el término de mayor grado (que es el que en el infinito marca la tendencia)
![]()
Dentro de cada una de ellas, no es difícil ver que:
- Dadas dos potencias de x la que tenga mayor exponente será un infinito de orden superior. En los polinomios se considera el término de mayor grado.
- Dadas dos funciones exponenciales con bases mayores que uno, la de mayor base es un infinito de orden superior.
- Dadas dos funciones logarítmicas, la de MENOR base será un infinito de orden superior.
EJERCICIOS RESUELTOS DE CÁLCULO DE LÍMITES POR COMPARACIÓN DE INFINITOS:
EJERCICIO M2BE1850; CASO DE INDETERMINACIÓN (∞/∞):
Calcular los siguientes límites:
RESOLUCIÓN DEL EJERCICIO:
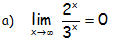
Ya que la exponencial del denominador es un infinito de orden superior al ser mayor la base.
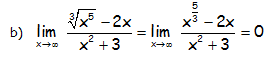
Ya que la potencial del denominador es un infinito de orden superior que la potencial del numerador.
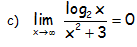
Ya que cualquier función potencial (polinómica) es un infinito de orden superior a cualquier logarítmica.
EJERCICIO M2BE1851; CASO DE INDETERMINACIÓN (∞-∞):
Calcular los siguientes límites:
RESOLUCIÓN DEL EJERCICIO:
![]()
Ya que el sustraendo es un infinito de orden superior al minuendo al ser mayor la base base.
![]()
Ya que la potencial del minuendo es un infinito de orden superior que la logarítmica del sustraendo.
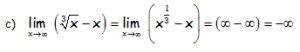
Ya que la función potencial (polinómica) del sustraendo es un infinito de orden superior a la del minuendo al tener mayor grado.


