INTEGRACIÓN DE FUNCIONES RACIONALES

INTEGRACIÓN DE FUNCIONES RACIONALES:

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:

SIGUE EL PROCESO DETERMINADO POR:

MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA

Y puede formar parte de: AYUDANDO A NUESTROS ALUMNOS QUE ESTÁN EN LA UNIVERSIDAD

Una función racional es un cociente de polinomio, con lo que estamos hablando del modo de resolver integrales del tipo:

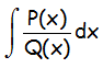
Donde tanto P(x) como Q(x) son polinomios.

Dependiendo tanto del grado de P(x) como de Q(x) y sobre todo de las raíces del denominador (de Q(x)), se distinguen diferentes casos:

I) Si el grado del numerador es mayor o igual que el del denominador:
II) Si el grado del numerador es menor que el grado del denominador:
- II.1) Si el denominador es de primer grado
- II.2) Si el denominador es de grado superior a uno, y al descomponerlo tiene RAÍCES REALES SIMPLES
- II.3) Si el denominador es de grado superior a uno, y al descomponerlo tiene RAÍCES REALES MÚLTIPLES
- II.4) Si el denominador al descomponerlo tiene RAÍCES IMAGINARIAS, a su vez se distinguen tres casos:
  - II.4.a) Numerador de grado cero y denominador de segundo grado
  - II.4.b) Numerador de primer grado y denominador de segundo grado
  - II.4.c) Denominador de grado superior a dos, con raíces imaginarias combinadas con reales

INTEGRALES RACIONALES: TIPOS Y PROPUESTAS PARA SU RESOLUCIÓN

I) SI EL GRADO DEL NUMERADOR ES MAYOR O IGUAL QUE EL DEL DENOMINADOR:

«Se hace la división», de forma algebraica clásica obteniendo el cociente C(x) y el resto R(x) para expresar la integral del siguiente modo, más sencilla de resolver:

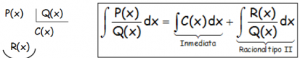
II) SI EL GRADO DEL NUMERADOR ES MENOR QUE EL GRADO DEL DENOMINADOR:

No hay que hacer la división y entramos ya en métodos de integración de funciones racionales.

Dependiendo del grado y de las raíces del denominador, se distinguen a su vez 4 casos:

II.1) SI EL DENOMINADOR ES DE PRIMER GRADO, la integral es directamente un logaritmo neperiano.

II.2) SI EL DENOMINADOR ES DE GRADO SUPERIOR A UNO, Y AL DESCOMPONERLO TIENE RAÍCES REALES SIMPLES:

Se descompone el denominador en factores, se utiliza el METODO DE LOS COEFICIENTES INDETERMINADOS y quedan integralitas inmediatas del tipo logaritmos neperianos.

EJERCICIO M2BE3241:

Resolver la siguiente integral:

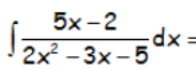
RESOLUCIÓN DEL EJERCICIO:

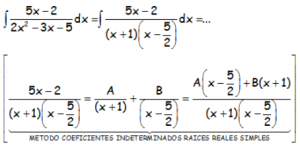
Identificando numeradores, ya que los denominadores son iguales:

Para encontrar los valores de A y B que cumplen esta realidad, podemos darle valores “convenientes” a la x, de tal modo que:

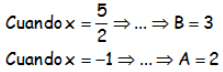
Con lo que ya podemos transformar la integral en suma de integralitas que serán logaritmos neperianos:

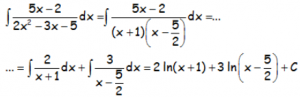
II.3) SI EL DENOMINADOR ES DE GRADO SUPERIOR A UNO, Y AL DESCOMPONERLO TIENE RAÍCES REALES MÚLTIPLES:

Lo mismo que en el caso anterior, pero hay que tener en cuenta que para los factores correspondientes a las raíces múltiples hay que considerar los de menor grado.

EJERCICIO M2BE3242:

Resolver la siguiente integral:

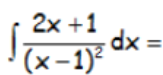
RESOLUCIÓN DEL EJERCICIO:

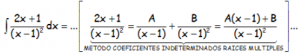
Identificaríamos los numeradores, igual que en el caso anterior y los valores convenientes en este caso sólo tenemos uno: x=1, con lo que una vez calculado B con este valor, hay que sustituirlo y tomar por ejemplo x=0 para hallar el valor de A.

Cuando hacemos esto, nos queda A=2; B=3, con lo que nos quedan dos integrales, un logaritmo neperiano y una potencial que se puede resolver por sustitución por ejemplo:

PARA LOS CASOS DE RAÍCES IMAGINARIAS, ES CONVENIENTE RECORDAR ALGUNAS COSILLAS DE LAS RAÍCES COMPLEJAS:

Cuando nos encontramos con un polinomio que tiene raíces imaginarias, a la hora de integrar interesa la siguiente transformación, teniendo en cuenta la forma en la que se puede descomponer en factores un polinomio:

Si al resolver una ecuación de segundo grado del tipo:

x² + bx + c =0

nos quedan soluciones imaginarias:

x₁ = α + βi

x₁ = α – βi

Podemos expresar el polinomio correspondiente en factores del siguiente modo:

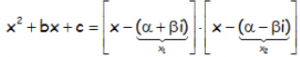
Y arreglándolo de manera conveniente para facilitar la expresión a integral:

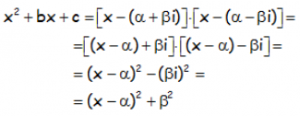
Estrategia que vamos a usar al referirnos a cada uno de estos tipos de integrales, porque ayuda a acercarnos a las integrales del TIPO ARCOTANGENTE.

TIPO II.4.a) NUMERADOR DE GRADO CERO Y DENOMINADOR DE SEGUNDO GRADO, CON RAÍCES IMAGINARIAS.

Intentamos llevar la integral a una arcotangente.

EJEMPLO GENERAL, PRÁCTICAMENTE UNA PLANTILLA:

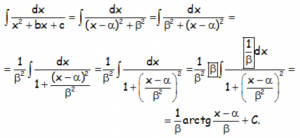
EJERCICIO M2BE117A:

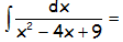
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EJERCICIOS RESUELTOS DE INTEGRALES RACIONALES

TIPO II.4.b) NUMERADOR DE PRIMER GRADO Y DENOMINADOR DE SEGUNDO GRADO CON RAÍCES COMPLEJAS:

Intentaremos llevar el numerador a la derivada del denominador, con estrategias básicas de poner-quitar-compensar, para obtener dos integralitas: una será un logaritmo neperiano y la otra del tipo II.4.a) anterior, una arcotangente.

EJEMPLO GENERAL, CASI UNA PLANTILLA PARA ESTE TIPO:

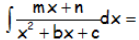
Notar como interesa que en el Numerador tengamos la expresión 2x+b (derivada del denominador), para llevar la integral a un logaritmo neperiano.

Lo siguiente refleja las estrategias para lograrlo, todas legales, matemáticamente hablando:

EJERCICIO M2BE117C:

Resolver la siguiente integral indefinida:

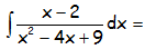
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EJERCICIOS RESUELTOS DE INTEGRALES RACIONALES

EJERCICIO M2BE118C:

Resolver la siguiente integral indefinida:

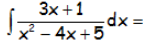
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EJERCICIOS RESUELTOS DE INTEGRALES RACIONALES

TIPO II.4.c) DENOMINADOR, DE GRADO SUPERIOR A DOS, CON RAÍCES IMAGINARIAS COMBINADAS CON REALES:

La complicación radica en que aparecen raíces reales combinadas con un factor irreducible de 2º grado. Para expresar la función racional como suma de fracciones más simples, en el método de los coeficientes indeterminados, nos obliga a colocar en el numerador de la fracción con denominador irreducible un polinomio de primer grado con dos coeficientes por conocer: Mx + N.

EJERCICIO M2BE3243:

Resolver la siguiente integral indefinida:

RESOLUCIÓN DEL EJERCICIO:

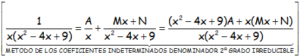
Notar el numerador de la fracción con denominador irreducible por tener raíces imaginarias.

Identificando numeradores y tomando valores para la x (son necesarios tres valores diferentes; uno de ellos x=0, los otros dos los que se desee), se obtiene:

Con lo que:

Post Views: 27