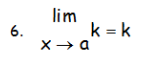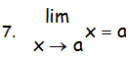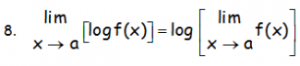PROPIEDADES LÍMITES FUNCIONES BACHILLERATO

PROPIEDADES DE LOS LÍMITES DE FUNCIONES PARA MATEMÁTICAS DE BACHILLERATO:PROPIEDADES LÍMITES FUNCIONES BACHILLERATO

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:

ESTÁ EN CONSONANCIA CON LAS ESTRATEGIAS DETERMINADAS POR LAS PROPUESTAS DE PROGRAMACIONES:

PROPIEDADES DE LOS LÍMITES DE FUNCIONES:

A poco que nos fijemos en las propiedades de los límites que se muestran, podemos observar que son profundamente intuitivas, en el sentido que si la operación implicada en el cálculo del límite tiene sentido, el mismo se puede descomponer del mismo modo que la operación.

No obstante, cuando nos encontramos con operaciones complicadas en cálculo de límites muy complejos, como por ejemplo cuando intentamos resolver un límite por INFINITÉSIMOS EQUIVALENTES, en ocasiones se hace necesario consultar estas propiedades de los límites para subdividirlo en límites más sencillos, sin cometer ninguna ilegalidad matemática.

PROPIEDADES:

1.- Si una función tiene límite en un punto, éste es único.

2.- Si los límites laterales de una función en un punto son diferentes, entonces la función no tiene límite en él. (Notar como esta propiedad está relacionada con la anterior)

3.- Si una función tiene límite distinto de cero en un punto, entonces existirá un entorno del mismo en el que los valores que toma la función tienen el mismo signo que el límite.

AL RESPECTO DE LAS OPERACIONES CON FUNCIONES A LAS QUE TENEMOS QUE CALCULAR EL LÍMITE:

Sean f(x) y g(x) dos funciones tales que existen los límites de cada una de ellas:

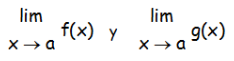
y sea k un número real cualquiera. Si f(x) y g(x) tienen límite, entonces se verifican, las siguientes propiedades:

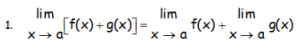
«El límite de la suma es igual a la suma de los límites»

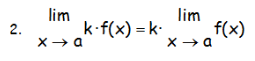
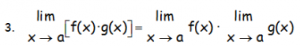
«El límite del producto es igual al producto de los límites»

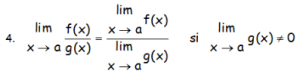
«El límite de un cociente de funciones es igual al cociente de los límites, siempre y cuando la operación tenga sentido -que no se anule el denominador- «

 

Post Views: 76
On: