TASA VARIACIÓN DERIVADA DEFINICIÓN
TASA DE VARIACIÓN MEDIA, INSTANTÁNEA, DERIVADA: DEFINICIÓN. EJERCICIOS RESUELTOS:

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- TABLA DE DERIVADAS
- INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA DE UNA FUNCIÓN EN UN PUNTO
- ANÁLISIS DE FUNCIONES PARA BACHILLERATO
- EJERCICIOS DE ANÁLISIS DE FUNCIONES CONTEXTUALIZADOS PARA MATEMÁTICAS DE BACHILLERATO
SIGUE EL ESQUEMA PLANTEADO PARA EL SEGUIMIENTO DE LA ASIGNATURA DE MATEMÁTICAS I DE 1º DE BACHILLERATO: MATEMÁTICAS I DE 1º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
SIGUE EL ESQUEMA PLANTEADO PARA EL SEGUIMIENTO DE LA ASIGNATURA DE MATEMÁTICAS II DE 2º DE BACHILLERATO: MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
DERIVADA: DEFINICIÓN:
DEFINICIÓN DE DERIVADA DE UNA FUNCIÓN EN UN PUNTO x=a:
Que también se denomina como tasa de variación instantánea en un punto x=a.
DEBEMOS CONOCER OTROS TÉRMINOS RELACIONADOS:
El cociente, sin el límite, se denomina TASA DE VARIACIÓN MEDIA:
El numerador solamente, se denomina TASA DE VARIACIÓN:
DEFINICIÓN DE FUNCIÓN DERIVADA:
Aquí no se particulariza para un valor «a» en concreto, sino que se obtiene la FUNCIÓN DERIVADA (en general).
Comentar que a la derivada también se le llama TASA DE VARIACIÓN INSTANTÁNEA
EJERCICIO DE OBTENCIÓN DE LA TASA DE VARIACIÓN MEDIA:
EJERCICIO M2BE3236, (Extraído del examen P.A.U. Canarias Extraordinaria-Julio 2025):
Para la función H(t) siguiente, donde se representa en número de hormigas de una colonia en función del tiempo en meses:
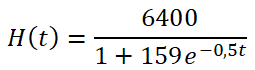
Obtener la TASA DE VARIACIÓN MEDIA, correspondiente al primer año, interpretando con rigor el resultado obtenido.
RESOLUCIÓN DEL EJERCICIO:
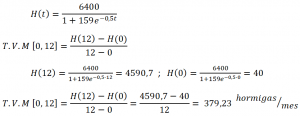
Que redondeando podemos decir, interpretando el resultado correctamente, que: el crecimiento del número de hormigas, en esa población, a lo largo del primer año ha sido de 379 hormigas por mes. Se podría denominar a este valor, tasa de crecimiento medio, ya que al ser un valor positivo es crecimiento, aumenta el número de hormigas. Si fuera negativo, diríamos: tasa de decrecimiento, en ese caso.
EJERCICIOS RESUELTOS DE OBTENCIÓN DE LA DERIVADA UTILIZANDO LA DEFINICIÓN:
EJERCICIO M1BE133:
Utilizando la definición de derivada, calcular la derivada de la función: f(x) = -2x+1
RESOLUCIÓN DEL EJERCICIO:
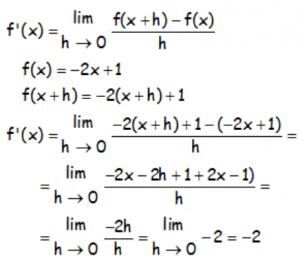
EJERCICIO M1BE164:
Utilizando la definición de derivada, calcular la derivada de la función: f(x)=2x+3
RESOLUCIÓN DEL EJERCICIO:
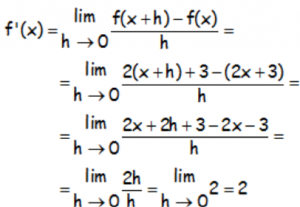
EJERCICIO M1BE216:
Utilizando la definición de derivada, calcular la derivada de la función f(x) = 2x2
RESOLUCIÓN DEL EJERCICIO:
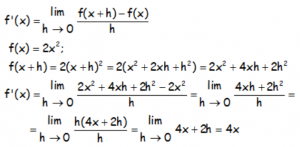
EJERCICIO M1BE194:
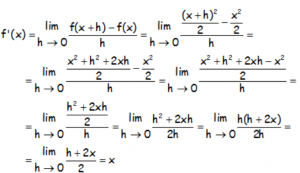
Utilizando la definición de derivada, calcular la derivada de la función:
RESOLUCIÓN DEL EJERCICIO:
EJERCICIO M1BE1969:
Obtener la derivada de la función: f(x)=x2+3x+1 , utilizando la definición de derivada.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/-So0Dr2frY4
EJERCICIO M1BE3126:
Realiza, utilizando la definición de derivada, la derivada de la siguiente expresión: f(x) = 2x2 – 4x
IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN RESUELTO DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA. PRUEBA 1 DEL TERCER TRIMESTRE DEL CURSO 2024-25
EJERCICIO M1BE2304:
Calcula la derivada de f(x) = 2x2+1 , utilizando la definición de derivada.
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: PROPUESTA DE EVALUACIÓN FUNCIONES 1º BACHILLERATO
EJERCICIO M1BE2473:
Utilizando la definición de derivada, obtener la derivada de la siguiente función:
f(x) = 3x2 + 5x
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN RESUELTO DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO. PRUEBA 1 DEL TERCER TRIMESTRE DEL CURSO 23-24.
EJERCICIO M1BE2193:
Utilizando la definición de derivada, obtener la derivada de las siguientes funciones: