EXAMEN ANÁLISIS DE FUNCIONES
MATEMÁTICAS II 2º BACHILLERATO
EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS II DE 2º BACHILLERATO (X661). GLOBAL PRIMER TRIMESTRE,
REALIZADO EN «EL PILAR»:
PUEDE INTERESAR LA CONSULTA DE:
ESTA PRUEBA SIGUE LA DINÁMICA QUE SE REFLEJA EN LA PROGRAMACIÓN PARA ESTE CURSO DE MATEMÁTICAS II DE 2º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA: MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
LOS ENUNCIADOS DE LA PRUEBA:
X661 EXAMEN ANÁLISIS FUNCIONES MATEMÁTICAS II BACHILLERATO (1)LOS EJERCICIOS DE LA PRUEBA Y SUS SOLUCIONES:
EJERCICIO M2BE2100:
Dividir un segmento de 6 cm de longitud en dos partes, con la propiedad de que la suma de las áreas del cuadrado y del triángulo equilátero construidos sobre ellos sea máxima.
LA RESOLUCIÓN DEL EJERCICIO A TRAVÉS DE VÍDEO:
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/UZpwBucitbk
EJERCICIO M2BE2288:
Calcular la siguiente integral indefinida:
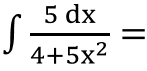
RESOLUCIÓN PASO A PASO DE ESTA INTEGRAL:
EJERCICIO M2BE2288 INTEGRAL ARCOTANGENTE V1
EJERCICIO M2BE2322:
Calcular la siguiente integral indefinida:
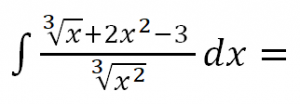
RESOLUCIÓN PASO A PASO DE ESTA INTEGRAL, COMO SI FUERA INMEDIATA:
EJERCICIO M2BE2322 INTEGRAL INMEDIATA SUSTITUCIÓN_v1
RESOLUCIÓN PASO A PASO DE ESTA INTEGRAL, POR SUSTITUCIÓN:
EJERCICIOM2BE2322 INTEGRAL SUSTITUCIÓN_v1
EJERCICIO M2BE2323:
Calcular la siguiente integral indefinida:
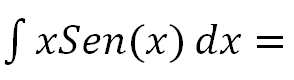
RESOLUCIÓN PASO A PASO DE ESTA INTEGRAL:
EJERCICIO M2BE2320:
Calcular la siguiente integral indefinida:
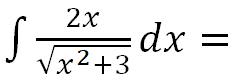
RESOLUCIÓN PASO A PASO DE ESTA INTEGRAL POR SUSTITUCIÓN:
RESOLUCIÓN PASO A PASO DE ESTA INTEGRAL COMO SI FUERA INMEDIATA:
EJERCICIO M2BE2320 INTEGRAL INMEDIATA_v1
EJERCICIO M2BE2316 (M2BE1992 AMPLIADO):
a.- Dada f(x), hallar los valores de m para que la función sea derivable en todo ℜ:
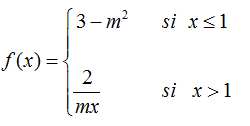
b.- Si m = 2, calcular la recta tangente a f(x) en x=3
LA RESOLUCIÓN DEL EJERCICIO:
IR AL VÍDEO QUE RESUELVE EL PRIMER APARTADO DEL EJERCICIO: https://youtu.be/YxFgioPnfdg
RESOLUCIÓN DEL SEGUNDO APARTADO DEL EJERCICIO:
EJERCICIO M2BE2316 RECTA TANGENTE_v1
EJERCICIO M2BE2321:
Un agricultor llamado Hortensio, quiere comprar un terreno rústico en Moya. El terreno, está delimitado por las funciones f(x) = x2 – 4x + 4 y g(x) = x. Suponiendo que el gráfico está en hectómetros:
a) Realiza un gráfico del terreno que quiere comprar Hortensio y sombréalo.
b) Calcula el precio del terreno, si cada hectómetro cuadrado en Moya tiene un valor de 150250 euros. Si Hortensio dispone de 600000 euros. ¿Puede comprarlo?