EJERCICIOS SOLUCIÓN PROPIEDADES LOGARITMOS
EJERCICIOS CON SOLUCIÓN DE UTILIZACIÓN DE LAS PROPIEDADES DE LOS LOGARITMOS:

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- EJERCICIOS DE APLICACIÓN DE LAS PROPIEDADES DE LOS LOGARITMOS. ARITMÉTICA PARA BACHILLERATO
- ARITMÉTICA PARA SECUNDARIA Y 1º DE BACHILLERATO
- UTILIDAD DE LOS LOGARITMOS. LEYES DE KEPLER
- ECUACIONES LOGARÍTMICAS PARA MATEMÁTICAS DE SECUNDARIA Y BACHILLERATO
- SISTEMAS DE ECUACIONES LOGARÍTMICAS
ESTE MATERIAL SIGUE EL PROCESO DETERMINADO POR:
- MATEMÁTICAS I DE 1º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
- MATEMÁTICAS DE 4º DE LA E.S.O.. DESARROLLO DE LA ASIGNATURA
DEFINICIÓN DE LA OPERACIÓN LOGARITMO:
![]()
CONSECUENCIAS DE LA DEFINICIÓN DE LOGARITMO:
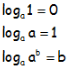
PROPIEDADES DE LOS LOGARITMOS:
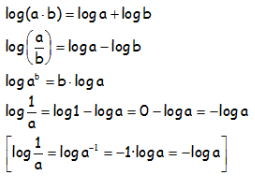
EJERCICIO M1BE1924:
Hallar sin calculadora el valor numérico de la siguiente expresión con logaritmos neperianos (logaritmos en base e).
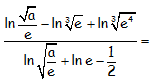
RESOLUCIÓN DEL EJERCICIO:
Utilizando la propiedad del logaritmo de un cociente y transformando la raíz del cociente del denominador en el cociente de raíces para poder utilizar posteriormente la misma propiedad de los logaritmos:
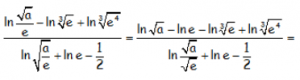
Utilizando de nuevo, la propiedad del logaritmo del cociente en el denominador y transformando las raíces en exponentes fraccionarios:
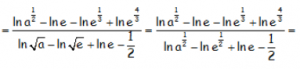
Utilizando la propiedad del logaritmo de una potencia, en la que el exponente queda multiplicando al logaritmo:
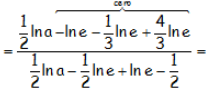
Teniendo en cuenta que además el [ln e=1]:
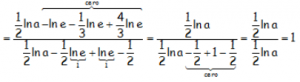
EJERCICIO M1BE1925:
Hallar sin calculadora, utilizando las propiedades de los logaritmos, el valor numérico de las siguientes expresiones con logaritmos en base dos:
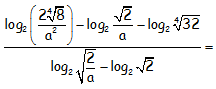
RESOLUCIÓN DEL EJERCICIO:
Utilizando en primer lugar la propiedad del logaritmo de un cociente y transformando las raíces en exponentes fraccionarios. En el denominador además transformaremos la raiz del cociente en un cociente de raíces, al mismo tiempo que transformaremos las raíces en exponentes fraccionarios, para poder utilizar la propiedad del logaritmo de una potencia:
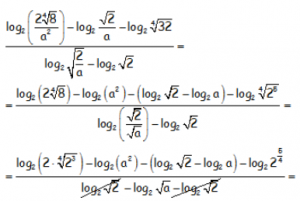
Transformando las raíces que nos quedan en exponentes fraccionarios, utilizando la propiedad del logaritmo de un producto en el primer término del numerador y la propiedad del logaritmo de una potencia donde se pueda y sobre todo sabiendo que [log2 2=1], nos queda:
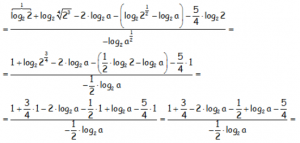
Agrupando los números que aparecen y los logaritmos de a que se puedan, al simplificar nos queda el resultado numérico buscado:
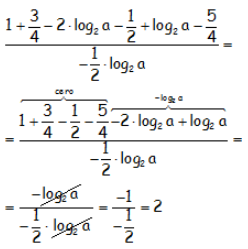
EJERCICIO M1BE1926:
Demostrar, desarrollando y utilizando las propiedades de los logaritmos, que la siguiente expresión con logaritmos decimales (en base 10), es equivalente a la mitad del logaritmo decimal de b.
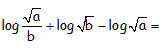
RESOLUCIÓN DEL EJERCICIO:
Utilizando las propiedades de los logaritmos, concretamente el logaritmo del cociente en el primer término y posteriormente transformando la raíz en exponente fraccionario para poder usar la propiedad del logaritmo de una potencia:
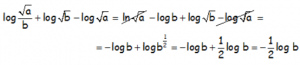
Se nos han ido los logaritmos de la raíz de a y efectivamente nos queda la mitad del logaritmo de b haciendo operaciones, PERO NO POSITIVO SINO NEGATIVO. Ojo a este tipo de cosas, tiene toda la pinta que nos han puesto este enunciado para confundir, ya que lo que demostramos es que en valor absoluto sí que cumple lo que nos dice el enunciado del ejercicio, pero con signo distinto, no resulta igual pero NEGATIVO.
EJERCICIO M1BE1927:
Demostrar con rigor, y basándose en las propiedades de los logaritmos, la veracidad o falsedad de la siguiente igualdad en logaritmos en base 3:
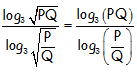
RESOLUCIÓN DEL EJERCICIO:
Transformando las raíces en exponentes fraccionarios para poder utilizar la propiedad del logaritmo de una potencia:
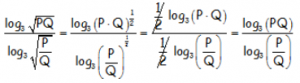
Notar como se simplifican las fracciones (1/2) quedando demostrada la veracidad de la igualdad.
