GEOMETRÍA PLANA MATEMÁTICAS BACHILLERATO

RECURSOS Y MATERIALES AUDIOVISUALES PARA MATEMÁTICAS DE SECUNDARIA Y 1º DE BACHILLERATO DE GEOMETRÍA PLANA (EN DOS DIMENSIONES):

ASPECTOS FORMALES LOMLOE PARA DOCENTES AL FINAL DEL ARTÍCULO, PARA NO INTERFERIR CON LO QUE ES DE INTERÉS PARA EL APRENDIZAJE DEL ALUMNADO

INTRODUCCIÓN TEÓRICA SOBRE LAS DIFERENTES FORMAS DE EXPRESAR LA ECUACIÓN DE UNA RECTA: VECTORIAL, PARAMÉTRICAS, CONTÍNUA, IMPLÍCITA O GENERAL, EXPLÍCITA, PUNTO-PENDIENTE:

VÍDEO EXPLICATIVO DE ESTA INTRODUCCIÓN A LAS DIFERENTES FORMAS DE EXPRESAR LA ECUACIÓN DE UNA RECTA EN GEOMETRÍA PLANA: https://youtu.be/uVS00IOsN_c

Se recomienda cuando se trabaje en casa o en clase, el contraste de los resultados obtenidos analíticamente con la representación gráfica de la situación en Geogebra para Ipad, o similar.

CIENCIA CON CONCIENCIA:

POSICIONES RELATIVAS DE DOS RECTAS EN EL PLANO:

Dos rectas en el plano se pueden cortar en un punto, ser paralelas o ser coincidentes.

Si imaginamos una recta como la línea que describe nuestra trayectoria, nuestra ruta a lo largo de la vida, ¿cómo te relacionas con los que te encuentras por el camino?.

¿Te has encontrado con otras «rectas coincidentes»?… o… ¿te has comportado como una recta paralela, manteniéndote siempre a una distancia prudencial de los que te has encontrado en el camino?. Ten en cuenta que para «coincidir» con otros hay que hacer un esfuerzo…

Y cuando tu recta se ha cortado con otra… ¿ha sido para bien?…

INTERIORIZO PROCESOS Y VALORES (PERFIL DE SALIDA DEL ALUMNADO)

CIENCIA CON CONCIENCIA

CLASE ON LINE DE GEOMETRÍA PLANA PARA 1º DE BACHILLERATO:

Clase on-line de geometría plana, para Matemáticas de 1º de Bachillerato de la Modalidad de Ciencias y Tecnología realizada en el Instituto «El Pilar», uno de los tres Institutos Diocesanos de Canarias.

La dinámica se realiza dentro del PROGRAMA DE MEJORA DEL APRENDIZAJE del Centro. Los alumnos que lo desean, fuera del horario lectivo, por la tarde, asisten a ella a través de Teams, en el equipo configurado al efecto. Se aporta aquí con la idea de que lo aprovechen incluso los que no han podido estar en tiempo real.

En la clase de hora y media de duración, de cuyo vídeo aportamos el enlace, se resuelven y se explican las siguientes cuestiones de geometría plana, todas contrastadas al final de su realización a través de Geogebra para Ipad:

EJERCICIO M1BE2370:

Partiendo del triángulo de vértices A(-6, -4), B(6,2) y C(-6,6), obtener el ORTOCENTRO (punto de intersección de las alturas).

Se calculan dos alturas y se obtiene el punto de intersección de ellas, resolviendo el sistema de ecuaciones correspondiente.

EJERCICIO M1BE2371:

Partiendo del triángulo de vértices A(8, 0), B(0,4) y C(-4,0), obtener el CIRCUNCENTRO (punto de intersección de las mediatrices).

Se calculan dos mediatrices y se obtiene el punto de intersección de ellas, resolviendo el sistema de ecuaciones correspondiente.

EJERCICIO M1BE2372:

Partiendo del triángulo de vértices A(7, 0), B(1,6) y C(-1,-2), obtener el BARICENTRO (punto de intersección de las medianas).

Se calculan dos medianas y se obtiene el punto de intersección de ellas, resolviendo el sistema de ecuaciones correspondiente.

EJERCICIO M1BE2373:

Partiendo del triángulo de vértices A(7, 0), B(1,6) y C(-1,-2), calcular la recta perpendicular al lado AC, que pase por el punto simétrico de A respecto de B.

EJERCICIO M1BE2374:

Hallar el área del triángulo de vértices A(7, 0), B(1,6) y C(-1,-2).

VÍDEO CON LA CLASE ON LINE DE GEOMETRÍA PLANA: https://youtu.be/sEPXSyKuCxk

PUNTOS Y RECTAS NOTABLES DE UN TRIÁNGULO

Ortocentro (H):Es el punto de corte de las tres alturas (cada una de las rectas perpendiculares trazadas desde un vértice al lado opuesto (o su prolongación).

Baricentro (G): Es el punto de corte de las tres medianas (Mediana es cada una de las rectas que une el punto medio de un lado con el vértice opuesto.

El baricentro divide a cada mediana en dos segmentos, el segmento que une el baricentro con el vértice mide el doble que el segmento que une baricentro con el punto medio del lado opuesto.

Circuncentro (O): Es el punto de corte de las tres mediatrices (Mediatriz es cada una de las rectas perpendiculares trazadas a un lado por su punto medio.

Es el centro de una circunferencia circunscrita al triángulo.

Incentro: Es el punto de corte de las tres bisetrices (Bisectriz es cada una de las rectas que divide a un ángulo en dos ángulos iguales.Es el centro de una circunferencia inscrita en el triángulo.

Recta de Euler: Une H, G, O

EJERCICIO M1BE1981:

Para el triángulo determinado por los tres puntos: A(1,4), B(-2,2) y C(3,1), hallar, en forma general las siguientes rectas:

A.- La ecuación de la recta que determina el lado BC.

B.- La ecuación de la recta perpendicular al lado BC, que pase por el punto C.

C.- La ecuación de la recta paralela al lado BC, que pase por el punto A.

VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/i-wIQ2wD65o

EJERCICIO M1BE2143:

Teniendo en cuenta que los puntos A(-1,2), B(3,4) y C(1,6) forman un triángulo, contestar a las siguientes cuestiones:

a.- Hallar la mediatriz del lado BC del triángulo. Expresar la ecuación de la recta en forma general.

b.- Hallar el punto simétrico de A respecto de C.

c.- Hallar una recta paralela al lado AC que pase por el origen de coordenadas, es decir, por el punto P(0, 0). Expresar la ecuación en forma explícita.

d.-Hallar una recta perpendicular al lado AC que pase por el punto Q(2, -3). Expresar la ecuación en forma punto pendiente.

IR AL ARTÍCULO CON LAS SOLUCIONES DE ESTE EJERCICIO: EXAMEN DE GEOMETRÍA PLANA 1º BACHILLERATO

EJERCICIO M1BE1976:

Para el triángulo determinado por los tres puntos: A(-1,7), B(2,8) y C(3,0), hallar las ecuaciones en forma general de las mediatrices del lado AC y del lado BC.

Posteriormente hallar el valor del circuncentro.

MEDIATRIZ DE UN SEGMENTO: RECTA PERPENDICULAR AL SEGMENTO QUE PASA POR SU PUNTO MEDIO.

CIRCUNCENTRO: PUNTO DE CORTE DE LAS MEDIATRICES DE LOS LADOS DE UN TRIÁNGULO

VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/-KzRhidKrUo

EJERCICIO M1BE1977:

Para el triángulo determinado por los tres puntos: A(-1,7), B(2,8) y C(3,0), hallar las ecuaciones en forma general de las alturas que parten del vértice A y del vértice B.

Posteriormente hallar el valor del ortocentro.

ALTURA DE UN TRIÁNGULO: RECTA PERPENDICULAR TRAZADA DESDE UN VÉRTICE AL LADO OPUESTO.

ORTOCENTRO: PUNTO DE CORTE DE LAS TRES ALTURAS DE UN TRIÁNGULO.

VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/dyme2WjR1Gs

EJERCICIO M1BE1978:

Para el triángulo determinado por los tres puntos: A(-1,7), B(2,8) y C(3,0), hallar las ecuaciones en forma general de las medianas que parten del vértice A y del vértice C.

Posteriormente hallar el valor del baricentro.

MEDIANA DE UN TRIÁNGULO: RECTA QUE UNE EL PUNTO MEDIO DE UN LADO CON EL VÉRTICE OPUESTO.

BARICENTRO: PUNTO DE CORTE DE LAS TRES MEDIANAS DE UN TRIÁNGULO.

VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/G4fQf99V8zI

EJERCICIO M1BE2144:

Calcula el baricentro del triángulo determinado por los puntos A(-1,2), B(3,4) y C(1,6).

IR AL ARTÍCULO CON LAS SOLUCIONES DE ESTE EJERCICIO: EXAMEN DE GEOMETRÍA PLANA 1º BACHILLERATO

EJERCICIO INTERDEPARTAMENTAL MAT-FYQ:

En un sistema de referencia cartesiano se sitúan dos masas: m₁=5 kg y m₂=6 kg, situadas respectivamente en los puntos (2,4) y (-4,0).

Hallar el vector fuerza gravitatoria en el punto medio del segmento que une las masas, supuestas las dos masas indicadas, aisladas y las únicas en el Universo .

DATO: G=6,67·10^-11 Unidades S.I.

PUEDE INTERESAR IR A FUERZAS GRAVITATORIAS EN DISTRIBUCIONES DE MASAS

EJERCICIO M1BE1979:

Para el triángulo determinado por los tres puntos: A(-1,1), B(2,3) y C(4,-2), hallar el área del triángulo, utilizando los conocimientos geométricos que se derivan de obtener la ecuación de la altura y de la base, así como los procesos implicados.

Ejercicio interesante, por la cantidad de aspectos de geometría plana que se ponen de manifiesto:

Una vez elegida la base, se obtiene lo que mide, haciendo el módulo del vector que une los dos puntos de la base.

Hay que obtener la ecuación de la recta que hace de base y la ecuación de la recta que hace de altura. Resolviendo este sistema de dos ecuaciones obtenemos el punto de intersección de la base con la altura. Con este punto podemos hallar lo que mide la altura haciendo el módulo del vector que une sus puntos.

Y ya podemos aplicar la fórmula del área de la base.

VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/wvlAksYqhL0

EJERCICIO M1BE2145:

Calcular el área del triángulo delimitado por los puntos A(-1,2), B(3,4) y C(1,6), considerando que la base es el lado que une los puntos A y B.

IR AL ARTÍCULO CON LAS SOLUCIONES DE ESTE EJERCICIO: EXAMEN DE GEOMETRÍA PLANA 1º BACHILLERATO

FÓRMULA DE HERÓN:

Es sencilla de utilizar y es perfecta para calcular el área de cualquier polígono complejo e incluso irregular, ya que podemos subdividir el polígono en triángulos y con esta fórmula hallar el área. Se necesita conocer lo que mide cada lado del polígono en cuestión.

Se puede usar para hallar el área de un solar o finca que no tiene que ser un polígono regular, siendo ésta una de las mejores utilidades en lo cotidiano.

Donde a, b y c son los lados del triángulo y “s” es el semiperímetro del triángulo.

La vamos a utilizar para resolver el ejercicio anterior, y así confirmar los resultados obtenidos con las herramientas geométricas.

EJERCICIO M1BE1980:

Para el triángulo determinado por los tres puntos: A(-1,1), B(2,3) y C(4,-2), hallar el área del triángulo, utilizando la fórmula de Herón.

VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/wT-m4-MszVg

EL ÁREA DE INFLUENCIA DEL VOLCÁN DE LA PALMA, LO HEMOS ESTIMADO SEGÚN EL TRIÁNGULO QUE FIGURA EN IMAGEN A CONTINUACIÓN (SUMINISTRADA POR GRAFCAN), DONDE SE INDICAN LOS LADOS DEL TRIÁNGULO. HALLAR LA SUPERFICIE QUE SE PUEDE CONSIDERAR INFLUENCIADA POR EL VOLCÁN EN NOVIEMBRE DE 2021, UTILIZANDO LA FÓRMULA DE HERÓN Y EXPRESARLA COMO NÚMERO DE CAMPOS DE FÚTBOL, PARA VISUALIZAR LA MAGNITUD DEL DESASTRE:

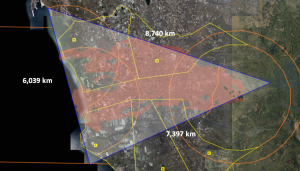
Los que tengan interés podrían incluso, aprovechando las distancias que se aportan, concretar más, generando triángulos de zonas no afectadas por la lava (uno al norte y otro al sur), para restárselos a esta área de influencia que hemos puesto nosotros.

Puede interesar, para ubicar la dinámica del proceso volcánico, el visionado de la siguiente animación, que corresponde a los primeros 80 días desde que comenzó la erupción. En ella se aporta el número de hectáreas alcanzadas por la lava: https://twitter.com/x_y_es/status/1468259061317656584?s=21

EJERCICIO M1BE2142:

Dado el triángulo de vértices: A(-1,1), B(2,3) y C(4,-2). Hallar el perímetro.

PROPUESTA DE TRABAJO T.B.L. PARA REALIZAR EN CLASE. APRENDIZAJE POR DESCUBRIMIENTO. EJERCICIOS M1BE2127:

TAREA M1BE2146:

Dibujar en clase, en la pizarra un vector cualquiera en el sistema cartesiano.

Pedir a los alumnos que digan las componentes cartesianas de un vector perpendicular al dado, que tenga el mismo módulo.
Una vez conseguido uno, que busquen otro.
Introducir el concepto de producto escalar, recordar la definición de trabajo en Física y reflexionar sobre lo interesante de la operación, que «desprecia» los comportamientos que no guardan una relación cinemática.
Indicar la receta para obtener un vector perpendicular a otro dado con esta estrategia del producto escalar.
Utilizar esta propuesta de trabajo para realizar el ejercicio:
Dados los puntos A(2,1) y B(4,5), hallar:
1. El vector AB
2. La distancia entre los dos puntos
3. El punto medio del segmento AB
4. La ecuación de la recta AB
5. La ecuación de la mediatriz del segmento AB (mediatriz: recta perpendicular al segmento AB que pasa por su punto medio), en todas las formas posibles.
6. La ecuación de una recta perpendicular a la recta AB que pase el punto A
7. Representar la situación en geogebra para IPAD o similar, a medida que se van obteniendo las rectas.
8. La ecuación de la recta (en todas las formas posibles) de una recta paralela al segmento AB, que pase por el origen.

https://es.wikipedia.org/wiki/Alfabeto_griego

EJERCICIO M1BE2348:

Hallar la ecuación de la recta, en todas las formas posibles, que pasa por los puntos A (2,-1) y B (4,2).

EJERCICIO M1BE2349:

Hallar la ecuación de la recta, que pasa por el puntos A (2,-1) y es paralela a 2y + 3x – 1 = 0.

Calcular el vector de la recta, encontrando dos puntos de la recta.

Obtener el término independiente de la recta.

EJERCICIO M1BE2350:

Hallar la ecuación de la recta, que pasa por el puntos A (2,-1) y es perpendicular a 2y + 3x – 1 = 0.

Calcular dos puntos de la recta, el vector de la recta y encontrar el perpendicular al anterior.

EJERCICIO M1BE2351:

Hallar la ecuación de la recta, que pasa por el punto A (2,-1) y por el punto medio del segmento determinado por los puntos B(0,3) y C(4,3).

EJERCICIO M1BE2352:

Hallar la ecuación de la recta, que pasa por el punto A (2,-1) y por el punto de corte de las rectas:

r: x+2y+3=0

s: y=x-1

EJERCICIO M1BE2134:

Para las rectas siguientes, indicar la posición relativa de cada una de las parejas posibles, argumentando analíticamente y razonadamente, aportando toda la información que se pueda.

r_A: (x,y)=(3,4)+t(-1,2)

r_B: 3x-y=2

r_C: pasa por el punto (2,-3) y tiene como vector director (1,-2)

EJERCICIO M1BE2135:

Indicar cuáles de las siguientes rectas:

r_A: (x,y)=(3,4)+t(-1,2)

r_B: 3x-y=2

r_C: pasa por el punto (2,-3) y tiene como vector director (1,-2)

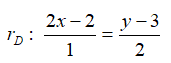
r_E: y=-x+1

a.- Pasa por el punto (o,1)

b.- Tiene pendiente m=-1

c.- Es paralela a la recta y=3x+1

d.- Tiene el vector (1,4) como vector dirección

e.- Es paralela a las rectas con pendiente m=-2

f.- Es perpendicular a las rectas con pendiente m=-1/2

g.- Pasa por el punto (2,2)

h.- Invéntate una pregunta difícil y similar, respóndela y coméntasela a tu profesor y si merece la pena, te la publicamos aquí. Claro… si perteneces a los Institutos Diocesanos.

EJERCICIOS M1BE2128:

Para un triángulo cualquiera, por ejemplo, se propone, el determinado por los puntos: A(2,3), B(5,1) y C(-1,-2), hallar alguna mediana, mediatriz y altura, utilizando la información al final de este artículo o el enlace: RECTAS Y PUNTOS NOTABLES EN UN TRIÁNGULO.

Se propone el siguiente orden y obteniendo la ecuación implícita de cada una de las rectas:

Ecuación de la mediana que pasa por A
Ecuación de la mediatriz del lado BC
Ecuación de la altura que pasa por C

Contrastar lo obtenido analíticamente con la aplicación geogebra o similar.

EJERCICIO M1BE2970:

En el triángulo determinado por los puntos: A(-2,-3); B(-1,5) y C(4,0), determinar, expresando la recta en forma general:

a.- La ecuación de la mediatriz del lado AB.

b.- La ecuación de la altura, tomando como base el lado AC.

c.- La ecuación de la mediana que pasa por el punto B.

d.- La ecuación de la recta paralela al lado BC y que pasa por A.

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EJERCICIO RESUELTO DE GEOMETRÍA PLANA PARA 1º DE BACHILLERATO: OBTENCIÓN DE MEDIATRIZ, ALTURA, MEDIANA EN UN TRIÁNGULO CUALQUIERA

EJERCICIO M1BE2366:

Considerando el triángulo de vértices A(-4,-1), B(0,3) y C(3,1), hallar:

a.- La distancia del lado AB (√13)

b.- La ecuación de la recta BC (2x+3y-9=0)

c.- La ecuación de la mediatriz del lado BC (6x-4y-1=0)

d.- La altura que pasa por A (3x-2y+10=0)

e.- La mediana que pasa por A (6x+3y-9=0)

f.- El área del triángulo. (10,01)

EJERCICIO M1BE2367:

Considerando el triángulo de vértices A(-4,-2), B(1,4) y C(6,1), hallar:

a.- El perímetro del triángulo. (√61+√34+√109)

b.- La ecuación del lado AB en forma general. (6x-5y+14=0)

c.- La ecuación del lado BC en forma paramétrica.(x=1+5t; y=4-3t)

d.- La ecuación del lado AC en forma explícita. (y=3/10x-4/5)

A partir de este apartado, todas las ecuaciones que se soliciten, expresarlas en forma general o implícita:

e.- La ecuación de la recta que pasa por A y es paralela al lado BC. (3x+5y+22=0)

f.- La ecuación de la recta que pasa por A y es perpendicular al lado BC. (5x-3y+14=0)

g.- La ecuación de la recta que tiene una pendiente m=3 y pasa por el origen. (3x-y=0)

h.- La ecuación de la recta que tiene una pendiente m=3 y pasa por el punto (-1,2). (3x-y+5=0)

i.- La ecuación de la altura que pasa por A. (5x-3y+14=0)

j.- La ecuación de la altura que pasa por B. (10x+3y-22=0)

k.- Obtener el punto intersección de las dos alturas anteriores y nombrarlo. (8/15,50/9) (ortocentro)

l.- La ecuación de la mediatriz del lado AB. (10x+12y+3=0)

ll.- La ecuación de la mediatriz del lado BC. (5x-3y-10=0)

m.- Obtener el punto de intersección de las dos mediatrices anteriores y nombrarlo.

n.- La ecuación de la mediana que pasa por A.

ñ.- La ecuación de la mediana que pasa por B.

o.- Obtener el punto de intersección de las dos medianas anteriores y nombrarlo.

p.-Hallar el área del triángulo, realizando los siguientes pasos:

p.1.- Hallar la base (tomando el lado AB)

p.2.- Hallar la ecuación de la altura.

p.3.- Hallar la ecuación de la base.

p.4.- Hallar el punto de corte de la altura y de la base (punto D).

p.5.- Hallar el valor de la altura, haciendo el módulo del vector CD.

p.6.- Dar el valor del área.

EJERCICIO M1BE2368:

Sea el triángulo formado por los puntos A(-6,-1), B(-1,4) y C(3,-3).

a.- Hallar la recta paralela a AB que pasa por el simétrico de B respecto de C.

s(7,-10); x-y-17=0

b.- Hallar la recta paralela a BC que pasa por el simétrico de B respecto de A.

s(-11,-6); 7x+4y+101=0

c.- Recta perpendicular al segmento AC que pasa por su punto medio. ¿Qué nombre recibe?

18x-4y+19=0

d.- Recta perpendicular al segmento AC que pasa por B. ¿Qué nombre recibe?

9x-2y+17=0

EJERCICIO M1BE2369:

Sea el triángulo formado por los puntos A(-4,-2), B(1,5) y C(4,-3).

a.- Hallar el baricentro.

(1/3, 0)

b.- Hallar el circuncentro.

(41/122. 23/122)

PUEDE INTERESAR IR A MÁS RECURSOS DE GEOMETRÍA, INCLUSO DE 2º DE BACHILLERATO, CON VÍDEOS EN GEOMETRÍA EN EL ESPACIO (3D): GEOMETRÍA PARA BACHILLERATO

ASPECTOS FORMALES PARA DOCENTES ACTUALIZADOS A LOMLOE:

SE PRETENDE CON ESTA DINÁMICA EL DESARROLLO DE LAS COMPETENCIAS: