CUESTIONES CON CIERTA COMPLICACIÓN DE GEOMETRÍA EN EL ESPACIO. RECTAS Y PLANOS

GEOMETRÍA ESPACIO 2º BACHILLERATO

CUESTIONES CON CIERTA COMPLICACIÓN DE GEOMETRÍA EN EL ESPACIO. RECTAS Y PLANOS:

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:

• • GEOMETRÍA ESPACIAL PARA BACHILLERATO

OBTENCIÓN DE RECTA PERPENDICULAR A OTRA, QUE PASE POR UN PUNTO, EN EL ESPACIO:

Si estuviéramos en el plano, como dos rectas que no sean paralelas terminan cortándose, si nos hicieran la siguiente pregunta, sería muy sencillo de responder:

EJERCICIO M1BE2148 (GEOMETRÍA EN EL PLANO):

Hallar la ecuación de la recta r, perpendicular a s que pase por el punto P(2,-3), siendo la recta s:

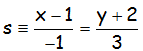
Teniendo en cuenta que la recta s está en forma contínua, los denominadores nos indican el vector director de la recta s, que es el vector (-1,3).

Por las propiedades del producto escalar, cuando intercambiamos componentes de un punto en el espacio y a una de ellas le cambiamos el signo, obtenemos un vector perpendicular a otro; el vector (3,1) es perpendicular al de la recta s dada.

Notar como el producto escalar (-1,3)·(3,1)=-3+3=0, efectivamente da cero.

Por ello el ejercicio se resuelve construyendo la recta directamente de la siguiente forma: con este vector perpendicular y pasando por el punto dado P(2,3), que en forma contínua:

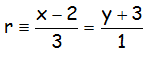
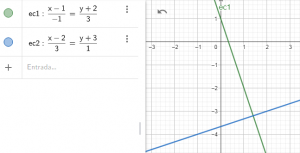
Que son claramente perpendiculares, como se observa en la representación con geogebra 2D:

Sin embargo, en el espacio en 3 dimensiones, la estrategia de fabricar un vector perpendicular a otro, intercambiando componentes, una de signo y además haciendo cero la otra, con la misma idea que en el plano, nos llevaría a una de las infinitas rectas que tienen como director uno perpendicular y pasan por el punto, pero casi con total probabilidad no exactamente a la recta que realmente la corta, que es la que buscamos.

Lo explicamos mejor en el ejercicio siguiente:

EJERCICIO M2BE2147:

Hallar la ecuación de la recta r perpendicular a la recta s, que pase por el punto P(1,-1,3), siendo s:

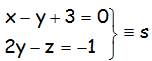
Como decimos, la complicación del ejercicio radica en el hecho de que si las rectas r y s tienen que ser perpendiculares, no basta con que sus directores sean perpendiculares, tienen que ser perpendiculares las rectas, lo que implica que tienen que cortarse.

Si no tuviéramos esto en cuenta y alegremente obtuviéramos un vector perpendicular al de la recta s (un vector cualquiera, haciendo el intercambio de dos componentes, una de signo y otra cero), y construyéramos la recta r pedida, con ese vector perpendicular y haciéndola pasar por el punto P, sólo tendríamos una de las infinitas rectas que con vector perpendicular al de s pasan por ese punto P. Pero no nos aseguraría que fuera la que concretamente corta a la recta s perpendicularmente.

El procedimiento tiene que ser otro: la propuesta que hacemos es:

1. Construir un plano π que sea perpendicular a s y que pase por el punto P.
2. Localizar el punto de corte Q del plano π con la recta s
3. Con ese punto Q (que pertenece a la recta dada s) y el punto P tendremos ya nuestra recta que cortando a s es perpendicular a ella, puesto que pertenece al plano π, que es perpendicular a s.

SOLUCIÓN DEL EJERCICIO:

EJERCICIO MIBE2147 solución

LA REPRESENTACIÓN DE LA SITUACIÓN QUE PUEDE SERVIR DE ACLARACIÓN:

OTRA FORMA DE OBTENER EL PUNTO Q, PARA EL MISMO EJERCICIO, UTILIZANDO UN PUNTO «X» GENÉRICO DE LA RECTA Y LAS PROPIEDADES DEL PRODUCTO ESCALAR, AUNQUE LO ADECUADO ES CENTRARSE EN UN ÚNICO PROCESO:

EJERCICIO M2BE2147 OTRA FORMA

EJERCICIO M2BE2149:

Siendo la recta r que se muestra y el punto A (0,-1,-2). Calcular la recta s perpendicular a r que pasa por A, expresándola en forma contínua.

SOLUCIÓN DEL EJERCICIO:

EJERCICIO M2BE2149 SOLUCION

EJERCICIO M2BE2150:

Se consideran los puntos A(2,-1,1) y B(-2,3,1) que determinan la recta r.

a.- Calcular la recta perpendicular a r que pasa por el punto P(-4,17,0)

b.- Calcular la ecuación del plano respecto del cual los puntos A y B son simétricos.

SOLUCIÓN: (x,y,z)=(-4,17,0)+(-6,-6,1)·t; -4x+4y-4=0

LA RESOLUCIÓN PASO A PASO DEL APARTADO A DE ESTE EJERCICIO:

EJERCICIO M2BE2150 A GEOMETRÍA ESPACIAL RECTA PERPENDICULAR_v1

LA RESOLUCIÓN PASO A PASO DEL APARTADO B DE ESTE EJERCICIO:

EJERCICIO M2BE2150 B GEOMETRÍA ESPACIAL__v1

EJERCICIO M2BE2424:

Teniendo en cuenta la recta r y el punto P(5, -6, -3), calcula la recta s que es perpendicular a r y pasa por el punto P, siendo r la recta siguiente:

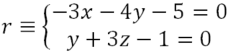
IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN TERCER TRIMESTRE MATEMÁTICAS II DE 2º DE BACHILLERATO: ANÁLISIS, ÁLGEBRA, GEOMETRÍA, PROBABILIDAD