LÍMITES INDETERMINACIONES NÚMERO e

UTILIZACION DEL NÚMERO e PARA RESOLVER INDETERMINACIONES DEL TIPO (1∞):
LÍMITES INDETERMINACIONES NÚMERO e

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:

ESTÁ EN CONSONANCIA CON LAS ESTRATEGIAS DETERMINADAS POR LAS PROPUESTAS DE PROGRAMACIONES:

Sabemos por las propiedades de los límites que:

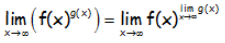
Si sucede que:

Una de las formas de solucionar la indeterminación es utilizando el número e (de Euler), que corresponde a su vez al límite siguiente:

El número e, es un número irracional, que es el límite de esa expresión y equivale a 2,71828182845904…

Ya que la función se puede adaptar, no sin dificultad a esa expresión del número e, del siguiente modo:

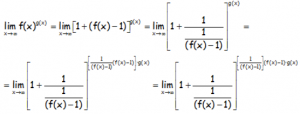
Con lo que resulta:

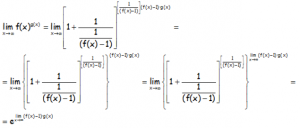
Resumiendo, la fórmula final:

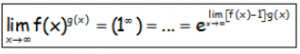
Que se puede utilizar para resolver indeterminaciones del tipo (1∞).

Que no es sino ir adaptando lo que nos piden, a la estructura del número e, ya que como se deduce de la definición del número e:

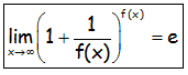
EJERCICIOS PROPUESTOS Y RESUELTOS:

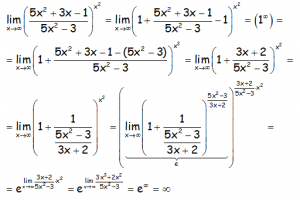
EJERCICIO M2BE1826:

Hallar el siguiente límite:


RESOLUCIÓN DEL EJERCICIO:

EJERCICIO M2BE1827:

Hallar el siguiente límite:


RESOLUCIÓN DEL EJERCICIO:

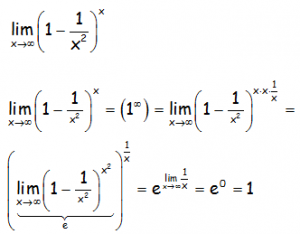
EJERCICIO M2BE1828:

Hallar el siguiente límite:

RESOLUCIÓN DEL EJERCICIO:

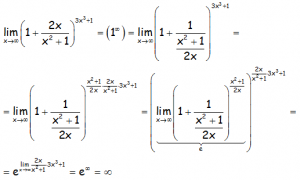
EJERCICIO M2BE2276 A:

Calcular el siguiente límite:

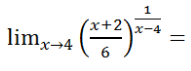
IR A LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS II DE 2º DE BACHILLERATO. CURSO 2023-24

EJERCICIO M2BE3330:

Realizar el siguiente límite:

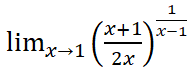
IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE MATEMÁTICAS II, 2º BACHILLERATO. ANÁLISIS DE FUNCIONES. PRUEBA 1 DEL PRIMER TRIMESTRE DEL CURSO 25-26

Visualizaciones: 219
On: