FUERZAS GRAVITATORIAS DISTRIBUCIONES MASAS
RELACIONADO CON GRAVITACIÓN EN EL UNIVERSO
FUERZAS GRAVITATORIAS EN DISTRIBUCIONES DE MASAS. OBTENCIÓN DE FUERZAS GRAVITATORIAS VECTORIALMENTE:
Desde el proyecto teníamos interés en publicar unos vídeos al respecto del tratamiento vectorial de las fuerzas gravitatorias, en distribuciones discretas de masas, evitando la complicación trigonométrica.
La obtención de fuerzas gravitatorias, y electrostáticas, en distribuciones discretas de masas, o de cargas, a nivel vectorial genera complicaciones la mayor parte de las veces como consecuencia de carencias en estrategias trigonométricas que pueden presentar los alumnos.
La expresión vectorial de la Ley de Gravitación Universal que proponemos en los dos videos que se muestran, evita la trigonometría, aunque es necesario algo de geometría vectorial.
Este contenido guarda mucha relación con el contenido propio de matemáticas para este nivel relacionado con vectores (Sentido Numérico), con lo que puede y debe verse como actividad interdepartamental.
ASPECTOS Y ELEMENTOS CURRICULARES LOMLOE PARA DOCENTES, AL FINAL DEL ARTÍCULO, PARA NO INTERFERIR CON LO QUE ES DE INTERÉS PARA NUESTROS ALUMNOS.
AL RESPECTO DE LA NOTACIÓN CIENTÍFICA:
TENER EN CUENTA QUE EN OCASIONES NO ES POSIBLE TENER UN EDITOR DE TEXTO DE NIVEL, O CALCULADORAS ANTIGUAS, CON LO QUE EN ESOS CASOS, o en PRUEBAS CON AUTOCORRECTOR, TIPO SOCRATIVE.
6,67·10-11 se expresa como 6.67E-11
NOTAR QUE NO SE PONE UNA COMA SINO UN PUNTO, TODO SIN ESPACIOS
NOTAR QUE UN NÚMERO DISTINTO DE CERO, SEGUIDO DEL PUNTO, Y DE DOS NÚMEROS REDONDEADO CONVENIENTEMENTE EL ÚLTIMO.
Si queremos expresar un vector, para no tener que poner el i y j con flechitas encima, podemos utilizar el sistema de componentes con un paréntesis, en plan: (3.34E-12,4.32E-11), componentes x e y del vector separados por una «,».
Así es como tendríamos que expresar un resultado en pruebas con autocorrección, tipo Socrative.
INTERESA LA CONSULTA DEL ARTÍCULO: LEY DE GRAVITACIÓN UNIVERSAL
EJERCICIO FQ1E2375:
Supongamos dos masas aisladas y puntuales: m1=1 kg situada en el punto (1,1) y m2=2 kg en el punto (4,2) de un sistema de referencia cartesiano, en el que las coordenadas están expresadas en metros. Para esta situación se pide el vector fuerza gravitatoria que la masa 1 hace sobre la masa 2 (F12).
DATO: G=6,67·10-11 Unidades S.I.
IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/luJ1hCMzXos
En el vídeo además se explica el modo de utilizar la LEY DE GRAVITACIÓN UNIVERSAL para obtener expresiones vectoriales de las FUERZAS GRAVITATORIAS.
EJERCICIO F2BE2113:
Disponemos en un sistema de referencia cartesiano, de dos masas: m1=1 kg y m2=2 kg , colocadas respectivamente en los puntos A (-2.1) y B (4,2). Las coordenadas están expresadas en metros.
A.- Hallar la Fuerza Gravitatoria que la masa 1 hace sobre la masa 2 (F12).
B.- Hallar la Fuerza Gravitatoria que la masa 2 hace sobre la masa 1 (F21).
DATO: G=6,67·10-11 Unidades S.I.
IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/_ynPnEunMrQ
EJERCICIO FQ1BE2376:
Supongamos tres masas aisladas y puntuales: m1=1 kg situada en el punto (-2,0) y m2=2 kg en el punto (3,1) y m3= 3 kg en el punto (2,-2) de un sistema de referencia cartesiano, en el que las coordenadas están expresadas en metros. Para esta situación se pide el vector fuerza gravitatoria que afectará a la masa 2 como consecuencia de la presencia de las masas 1 y 3.
DATO: G=6,67·10-11 Unidades S.I.
IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/jpk6g1N-VKo
EJERCICIO FQ1BE2670:
Disponemos de tres masas aisladas y puntuales, que suponemos las únicas del Universo: m1=1 kg situada en el punto (2,0) y m2=2 kg en el punto (5,-4) y m3= 3 kg en el punto (1,3) de un sistema de referencia cartesiano, en el que las coordenadas están expresadas en metros. Para esta situación se pide:
a.- Hallar la fuerza que la masa 1 hace sobre la masa 3 (vector y módulo).
b.- Hallar la fuerza que la masa 2 hace sobre la masa 3 (vector y módulo).
c.- Hallar la fuerza resultante sobre la masa 3 (vector y módulo).
DATO: G=6,67·10-11 Unidades S.I.
EJERCICIO FQ1BE2377:
Disponemos en un sistema de referencia cartesiano, de tres masas: m1=1 kg y m2= 2 kg , m3=3 kg, colocadas respectivamente en los puntos A (-1,2), B (0,4) y C(3,1), estando las componentes expresadas en metros.
a.- Dibujar con el rigor esperado en este nivel, las masas en el sistema cartesiano, las fuerzas que actúan sobre la masa m3, así como obtener gráficamente la fuerza resultante sobre la masa m3, utilizando correctamente la regla del paralelogramo con las fuerzas implicadas sobre m3.
b.- Obtener vectorialmente la fuerza gravitatoria que la masa 1 hace sobre la masa 3.
c.- Obtener vectorialmente la fuerza gravitatoria que la masa 2 hace sobre la masa 3.
d.- Hallar la fuerza gravitatoria (vector y módulo) a la que se encuentra sometida la masa 3 como consecuencia de la presencia de las otras dos masas.
DATO: G=6,67·10-11 Unidades S.I.
IR AL ARTÍCULO CON LA RESOLUCIÓN DETALLADA DEL EJERCICIO: EJERCICIO RESUELTO (FQ1BE2377) DE FUERZAS GRAVITATORIAS EN DISTRIBUCIONES DISCRETAS DE MASAS, PARA FÍSICA DE BACHILLERATO. CAMPO GRAVITATORIO
EJERCICIO FQ1BE3055:
Disponemos en un sistema de referencia cartesiano, de tres masas: m1=1,7 kg y m2= 0,8 kg , m3= 750 g, colocadas respectivamente en los puntos A (-3,-2), B (-2,3) y C(4,-1), estando las componentes expresadas en metros.
a.- Dibujar con el rigor esperado en este nivel, las masas en el sistema cartesiano, las fuerzas que actúan sobre la masa m2, así como obtener gráficamente la fuerza resultante sobre la masa m2, utilizando correctamente la regla del paralelogramo con las fuerzas implicadas sobre m2.
b.- Obtener vectorialmente la fuerza gravitatoria que la masa 1 hace sobre la masa 2.
c.- Obtener vectorialmente la fuerza gravitatoria que la masa 3 hace sobre la masa 2.
d.- Hallar la fuerza gravitatoria (vector y módulo) a la que se encuentra sometida la masa 2 como consecuencia de la presencia de las otras dos masas.
DATO: G=6,67·10-11 Unidades S.I.
IR AL ARTÍCULO CON LA RESOLUCIÓN DETALLADA DEL EJERCICIO: EJERCICIO RESUELTO DE FUERZAS GRAVITATORIAS EN DISTRIBUCIONES DE MASAS
EJERCICIO FQ1BE2175:
En un sistema de referencia cartesiano, se sitúan dos masas puntuales: m1 de 1 kg de masa y colocada en el punto (-1,2) y m2 de 2 kg situada en el punto (3,0).
Hallar para esta distribución discreta de masas y supuesta aislada del resto del universo, el vector Fuerza Gravitatoria que la masa 1 ejerce sobre la masa 2.
DATO: G=6.67·10-11 N·m2·kg-2
IR AL VIDEO QUE RESUELVE EL EJERCICIO, UTILIZANDO LA EXPRESIÓN VECTORIAL DE LA LEY DE GRAVITACIÓN UNIVERSAL: https://youtu.be/_w7Y5P47Qys
IR AL VÍDEO QUE RESUELVE EL EJERCICIO, PERO UTILIZANDO EN ESTE CASO LA TRIGONOMETRÍA, QUE ES COMO LE GUSTA A ALGUNOS PROFESORES QUE SE RESUELVA: https://youtu.be/Iy-zBBQ3P4k
EJERCICIO FQ1BE2378:
Disponemos en un sistema de referencia cartesiano, de tres masas puntuales y aisladas: m1=400 g y m2= 1,2 kg , m3=3 kg, colocadas respectivamente en los puntos A (0,3), B (1,1) y C(-3,0). Las coordenadas están expresadas en metros.
a.- Hallar el vector fuerza gravitatoria que la masa 1 hace sobre la masa 2 (F12).
b.- Hallar el vector fuerza gravitatoria que la masa 3 hace sobre la masa 2 (F32).
c.- Hallar el vector fuerza gravitatoria resultante que las masas 1 y 3 hacen sobre la masa 2 (F2).
d.- Hallar el módulo de la fuerza gravitatoria que sufre la masa 2 consecuencia de la distribución de masas del enunciado.
e.- Hallar la aceleración (vector y módulo) a la que se verá sometida la masa 2 como consecuencia de la distribución de masas del enunciado.
DATO: G=6,67·10-11 Unidades S.I.
SOLUCIONES: -2.86E-12 i +5.73E-12 j (N); -1.37E-11 i -3.43E-12 j (N); -1.66E-11 i + 2.3E-12 j (N): 1.65E-11 N; -1.38E-11 i + 1.92E-12 j (m/s2); 1.4E-11 (m/s2)
EJERCICIO INTERDEPARTAMENTAL MAT-FYQ:
En un sistema de referencia cartesiano se sitúan dos masas: m1=5 kg y m2=6 kg, situadas respectivamente en los puntos (2,4) y (-4,0).
Hallar el vector fuerza gravitatoria en el punto medio del segmento que une las masas, supuestas las dos masas indicadas, aisladas y las únicas en el Universo .
DATO: G=6,67·10-11 Unidades S.I.
PUEDE INTERESAR IR A GEOMETRÍA PLANA PARA 1º DE BACHILLERATO
EJERCICIO F2BE2343:
Disponemos de dos planetas de masas M1 y M2 respectivamente, siendo la masa M1 seis veces mayor que M2.
Supongamos que la masa M1 se encuentra a la izquierda de M2.
Si la distancia entre ambos planetas es de 6·106 km, ¿a qué distancia de M1 y en medio de los dos planetas, se encuentra el punto donde la fuerza que ejerce M1 será la tercera parte de la que ejerce M2.
DATO: G=6,67·10-11 Unidades S.I.
SOLUCIÓN: 4.86E9 m
EJERCICIO F2BE2625:
Para la siguiente distribución de masas, supuestas aisladas y las únicas del Universo, en los puntos del S.R. cartesiano habitual, donde las coordenadas están expresadas en metros:
m1 = 2 kg en (3,0); m2 = 1 kg en (-3, -3) y m3 = 4 kg en (0,3)
Responder a las siguientes preguntas, dejando reflejados en el diagrama los vectores que se solicitan:
a.- Vector y módulo del campo gravitatorio creado por la masa 1 en el origen del sistema de referencia, punto (0,0).
b.- Vector y módulo del campo gravitatorio creado por la masa 2 en el origen.
c.- Vector y módulo del campo gravitatorio resultante, que las tres masas crean en el origen.
d.- Vector y módulo de la fuerza gravitatoria que la masa 1 hace sobre la masa 2.
DATOS: G=6.67×10-11 Nm2kg-2
IR A LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN INICIAL PARA FÍSICA DE 2º DE BACHILLERATO: CAMPO GRAVITATORIO Y GRAVITACIÓN EN EL UNIVERSO. EJERCICIOS RESUELTOS
EJERCICIO F2BE2844:
En un sistema de referencia cartesiano, donde las coordenadas se suponen en metros, se sitúa una masa m , aislada y la única del Universo, de 200 kg de masa en el punto (3, -2). (2 puntos)
a.- Hallar el vector intensidad de campo gravitatorio en el punto P (-1, 3).
b.- Hallar el módulo del vector intensidad de campo, a través de las componentes del vector obtenido y utilizando la expresión que corresponde a la definición del vector intensidad de campo gravitatorio a partir de la fuerza gravitatoria por unidad de masa en el punto.
Datos: G = 6,67·10 -11 U.S.I.
IR A LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN RESUELTO DE FÍSICA DE 2º DE BACHILLERATO. CURSO 2024-25. PRIMER TRIMESTRE. CAMPO GRAVITATORIO Y GRAVITACIÓN
EJERCICIO F1BE2673:
En un sistema de referencia cartesiano, en el que las coordenadas se suponen indicadas en metros, se sitúan dos masas: m1=3 kg en el punto (-3,2) y m2=4 kg en el punto (4,0).
En esta situación se pide, indicando en el sistema de referencia cada uno de los vectores solicitados:
a.- El vector de posición de la masa 1.
b.- El vector de posición de la masa 2 .
c.- El vector fuerza gravitatoria que la masa 1 hace sobre la masa 2, y su módulo.
d.- La aceleración que experimentará la masa 2 como consecuencia de la acción de la fuerza del apartado anterior sobre ella en módulo.
e.- El vector fuerza gravitatoria que la masa 2 hace sobre la masa 1 y su módulo.
DATO: G=6,67·10-11 u.S.I.
IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE FUERZAS GRAVITATORIAS EN DISTRIBUCIONES DE MASAS
EJERCICIO FQ1BE2802:
En un sistema de referencia cartesiano donde las distancias están en unidades del S.I. situamos dos masas del siguiente modo, m1 de 1kg en el punto (4,-2) y m2 de 2 kg en el punto (0,3).
a.- Hallar la distancia entre las masas (1 punto)
b.- El vector fuerza gravitatoria que la masa 1 hace sobre la masa 2 (F12). (2 puntos)
c.- El vector fuerza gravitatoria que la masa 2 hace sobre la masa 1. (1 puntos)
d.- Dibujar e indicar claramente las fuerzas que se solicitan en los dos apartados anteriores. (1 p.)
DATOS: G=6,67·10-11 u.S.I.
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: PRUEBA FINAL RESUELTA DE CONTENIDOS DE FÍSICA. PARA FÍSICA Y QUÍMICA DE 1º DE BACHILLERATO. CURSO 2023-24
EJERCICIO F1BE2674:
En un sistema de referencia cartesiano, en el que las coordenadas se suponen indicadas en metros, se sitúan dos masas: m1=3 kg en el punto (-3,2) y m2=4 kg en el punto (4,0).
En esta situación se pide, indicando en el sistema de referencia cada uno de los vectores solicitados:
a.- El vector de posición de la masa 1.
b.- El vector de posición de la masa 2.
c.- El vector fuerza gravitatoria que la masa 2 hace sobre la masa 1, y su módulo.
d.- La aceleración que experimentará la masa 1 como consecuencia de la acción de la fuerza del apartado anterior sobre ella en módulo.
e.- El vector fuerza gravitatoria que la masa 1 hace sobre la masa 2 y su módulo.
DATO: G=6,67·10-11 u.S.I.
IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE FUERZAS GRAVITATORIAS EN DISTRIBUCIONES DE MASAS
EJERCICIO FQ1BE2703:
En un sistema de referencia cartesiano, en el que las coordenadas se suponen indicadas en metros, se sitúan dos masas: m1=200 g en el punto (-2,3) y m2=1,5 kg en el punto (3,0).
En esta situación se pide, indicando en el sistema de referencia cada uno de los vectores solicitados:
a.- El vector fuerza gravitatoria que la masa 1 hace sobre la masa 2.
b.- El vector fuerza gravitatoria que la masa 2 hace sobre la masa 1
(-5.05E-13, 3.03E-13); (5.05E-13, -3.03E-13)
EJERCICIO FQ1BE2849:
En un sistema de referencia cartesiano, en el que las coordenadas se suponen indicadas en metros, se sitúan tres masas: m1=3 kg en el punto (-3,2) y m2=4 kg en el punto (4,0) y m3=900 g en el punto (3,4).
En esta situación se pide, indicando en el sistema de referencia cada uno de los vectores solicitados:
a.- El vector fuerza gravitatoria que la masa 1 hace sobre la masa 3.
b.- El fuerza resultante que resulta sobre la masa 3 como consecuencia de la presencia de las otras dos masas.
e.- El módulo de la aceleración que sufre la masa 3 como consecuencia de la presencia de las otras dos masas.
DATO: G=6,67·10-11 u.S.I.
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN RESUELTO DE GRAVITACIÓN, FUERZAS GRAVITATORIAS Y MOVIMIENTO CIRCULAR UNIFORME, PARA FÍSICA Y QUÍMICA DE 1º DE BACHILLERATO
EJERCICIO FQ1BE3361:
Disponemos en un sistema de referencia cartesiano, de tres masas: m1=5 kg y m2= 7 kg , m3= 8 kg, colocadas respectivamente en los puntos A (0, 4), B (0, -4) y C(3, 2), estando las componentes expresadas en metros y considerándolas aisladas y las únicas del Universo.
a.- Dibujar con el rigor esperado en este nivel, las masas en el sistema cartesiano, las fuerzas que actúan sobre la masa m1, así como obtener gráficamente la fuerza resultante sobre la masa m1, utilizando correctamente la regla del paralelogramo con las fuerzas implicadas sobre m1.
b.- Obtener vectorialmente la fuerza gravitatoria que la masa 2 hace sobre la masa 1.
c.- Obtener vectorialmente la fuerza gravitatoria que la masa 3 hace sobre la masa 1.
d.- Hallar la fuerza gravitatoria a la que se encuentra sometida la masa 1 como consecuencia de la presencia de las otras dos masas.
e.- Hallar la aceleración a la que se encontrará sometida la masa 1, como consecuencia de la distribución de masas.
DATO: G=6,67·10-11 Unidades S.I.
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO FQ1BE3361 DE FUERZAS GRAVITATORIAS Y ACELERACIÓN EN DISTRIBUCIONES DE MASAS
EJERCICIO F2BE3210:
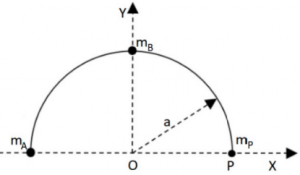
Sobre un arco de circunferencia se depositan tres partículas de 40 g de masa, según se muestra en la figura. Teniendo en cuenta que a = 8 cm, calcule y dibuje el vector fuerza gravitatoria que experimenta la partícula situada en el punto P.
Dato: G=6,67·10-11 N·m2/kg2
IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTE EJERCICIO DE PAU CANARIAS: EXAMEN DE FÍSICA 2º BACHILLERATO, P.A.U. CANARIAS JULIO 2025. CONVOCATORIA EXTRAORDINARIA
EJERCICIO F2BE3200:
En el punto A (2,0) se sitúa una masa de 2 kg y en el punto B (5,0) se coloca otra de 4 kg. Si las longitudes se miden en metros:
a) Calcule el potencial del campo gravitatorio en el punto C (2,4).
b) Si se sitúa una masa de 1 kg en el origen de coordenadas, calcule el vector fuerza resultante que actúa sobre ella y el trabajo realizado para llevar esa masa desde el origen de coordenadas hasta el infinito.
DATO: G = 6,67·10-11 N·m2/kg2
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXÁMENES DE FÍSICA 2º BACHILLERATO, P.A.U. CANARIAS JUNIO 2025
PODRÍA INTERESAR CONTINUAR CON EL SIGUIENTE ENLACE, DE ESTA MISMA WEB, DE EJERCICIOS DE OBTENCIÓN DEL VECTOR INTENSIDAD DE CAMPO GRAVITATORIO Y ELECTROSTÁTICO: INTENSIDAD DE CAMPO GRAVITATORIO Y ELECTROSTÁTICO
ASPECTOS FORMALES PARA DOCENTES:
CON RESPECTO A LOS SABERES BÁSICOS DE FÍSICA Y QUÍMICA DE 1º BACHILLERATO PREDOMINANTES EN LA ACTIVIDAD:
CON RESPECTO A LAS COMPETENCIAS ESPECÍFICAS DE FÍSICA Y QUÍMICA DE 1º DE BACHILLERATO QUE SE CONSIDERAN:
FYQ 1BAC C1 , FYQ 1BAC C2 , FYQ 1BAC C3 , FYQ 1BAC C4 , FYQ 1BAC C5 , FYQ 1BAC C6
VINCULADOS A LOS DESCRIPTORES OPERATIVOS de las Competencias Clave CORRESPONDIENTES
CON RESPECTO A LAS COMPETENCIAS CLAVE Y DESCRIPTORES OPERATIVOS ASOCIADOS:
-
- COMPETENCIA MATEMÁTICA Y EN CIENCIA, TECNOLOGÍA E INGENIERÍA (STEM), concretamente los DESCRIPTORES OPERATIVOS STEM1 , STEM2 , STEM4
- COMPETENCIA EN CONCIENCIA Y EXPRESIÓN CULTURALES (CCEC), concretamente el DESCRIPTOR OPERATIVO CCEC2 y EL DESCRIPTOR OPERATIVO CCEC4.2
- COMPETENCIA EN COMUNICACIÓN LINGÜÍSTICA (CLL), concretamente los DESCRIPTORES OPERATIVOS CCL2 , CCL3.
- COMPETENCIA DIGITAL (CD), concretamente el DESCRIPTOR OPERATIVO CD1 y CD3
- COMPETENCIA EMPRENDEDORA (CE), concretamente el DESCRIPTOR OPERATIVO CE1
- COMPETENCIA PERSONAL, SOCIAL Y DE APRENDER A APRENDER (CPSAA), concretamente el DESCRIPTOR OPERATIVO CPSAA1.1 , CPSAA4 , CPSAA5
CON RESPECTO A LOS CRITERIOS DE EVALUACIÓN, VINCULADOS A LAS CORRESPONDIENTES COMPETENCIAS ESPECÍFICAS:
FYQ1BAC1.1 , FYQ1BAC1.2 , FYQ1BAC2.3 , FYQ1BAC3.1 , FYQ1BAC3.3 , FYQ1BAC6.1
Incluyen los descriptores operativos asociados
SE CONTEMPLAN LOS ASPECTOS RELACIONADOS CON EL PERFIL DE SALIDA DEL ALUMNADO DE LOS INSTITUTOS DIOCESANOS DE CANARIAS
PODRÍA INTERESAR LA VISITA AL SIGUIENTE ARTÍCULO DEL PROYECTO, DONDE SE DESARROLLAN LAS ASIGNATURAS DE FÍSICA Y QUÍMICA DE SECUNDARIA Y BACHILLERATO: