EXAMEN RESUELTO GRAVITATORIO ELECTROMAGNETISMO
SEGUNDO BACHILLERATO PRUEBA RESUELTA FÍSICA
EXAMEN RESUELTO CON EJERCICIOS DE CAMPOS GRAVITATORIO, ELECTROSTÁTICO Y MAGNÉTICO (ELECTROMAGNETISMO), CORRESPONDIENTE A PRUEBA 1 DEL PRIMER TRIMESTRE 2025-26, PARA FÍSICA DE 2º DE BACHILLERATO (X1071), REALIZADA EN EL PILAR:

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES MATERIALES RELACIONADOS CON ESTA PRUEBA DENTRO DE ESTE PROYECTO DE MEJORA DEL APRENDIZAJE EN CIENCIAS:
SIGUE EL PROCESO DETERMINADO POR EL DESARROLLO DE LA ASIGNATURA DE FÍSICA DE 2º DE BACHILLERATO DE ESTE PROYECTO DE MEJORA DEL APRENDIZAJE EN CIENCIAS: FÍSICA DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
PUEDE INTERESAR LA CONSULTA DE LOS EXÁMENES RESUELTOS PARA FÍSICA DE 2º DE BACHILLERATO PUBLICADOS EN EL SIGUIENTE ENLACE: EXÁMENES RESUELTOS DE FÍSICA 2º BACHILLERATO
EL ENUNCIADO DE ESTA PRUEBA DE CAMPOS GRAVITATORIO, ELÉCTRICO Y MAGNÉTICO (ELECTROMAGNETISMO), QUE INCLUYE ASPECTOS DE AUTOEVALUACIÓN E INFORMACIÓN DE RETORNO (FEED-BACK DEL ALUMNADO):
LOS EJERCICIOS DE LA PRUEBA Y SU RESOLUCIÓN PASO A PASO:
EJERCICIO F2BE2691:
a.- Obtener la altura de la órbita geoestacionaria, haciendo con rigor todos los desarrollos y razonamientos necesarios, indicando la utilidad de situar satélites a esa altura.
b.- Hallar la energía total de un satélite de 500 kg orbitando en esa órbita geoestacionaria.
c.- Hallar la energía que hay que comunicarle al satélite del apartado anterior para que pase a otra órbita situada a 40000 km de la superficie de la Tierra.
DATOS: G=6,67·10-11 Nm2kg-2; MTierra=5,97·1024 kg; RTierra=6370 km.
RESOLUCIÓN DE ESTE EJERCICIO DE GRAVITACIÓN EN EL UNIVERSO:
EJERCICIO F2BE3340:
En cada uno de los tres vértices de un triángulo isósceles, de base 6 cm y teniendo cada uno de los dos lados iguales una longitud de 5 cm, se depositan cargas q1, q2 y q3 con los siguientes valores y en las posiciones indicadas en el diagrama: q1 = 1 µC; q2 = – 2 µC; q3= – 3 µC.
Respetando la colocación en el sistema de referencia que se muestra y suponiendo que las coordenadas se expresan en metros, responder a las siguientes cuestiones: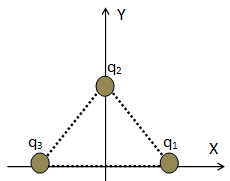
a.- Dibujar claramente los campos eléctricos que cada una de las cargas genera en el origen, así como aproximadamente el campo eléctrico total.
b.- Obtener los vectores campo eléctrico parciales y total del apartado anterior.
c.- Hallar el potencial eléctrico en el origen del sistema de referencia.
d.- Hallar el trabajo que realizan las fuerzas del campo para trasladar una carga q4 de 4 µC, desde el origen al infinito, interpretando con rigor el resultado obtenido.
e.- Enunciar y formular la Ley de Coulomb y utilizarla para obtener las unidades de la constante eléctrica.
K = 9·109 u.S.I.
RESOLUCIÓN DE ESTE EJERCICIO DE CAMPO ELÉCTRICO (ELECTROSTÁTICA):
EJERCICIO F2BE3341:
Mediante una diferencia de potencial de 2750 V, se aceleran electrones, de tal manera que llevan la dirección del eje OY en sentido negativo. Conocemos que en la zona existe un campo magnético de 1,2 T en la dirección del eje OX sentido positivo.
a.- Hallar la velocidad que adquiere el electrón como consecuencia de aplicarle esa diferencia de potencial.
b.- Dibujar en el sistema de ejes cartesianos la situación con los vectores implicados: velocidad, campo magnético y fuerza magnética.
c.- Hallar la fuerza magnética a la que se verá sometido el electrón, vector y módulo.
DATOS: qe- = -1.6·10-19 C ; me=9,11·10-31 kg.
RESOLUCIÓN DE ESTE EJERCICIO DE CAMPO MAGNÉTICO DE APLICACIÓN DE LA LEY DE LORENTZ:
