INTEGRALES DERIVADAS PROBLEMAS CONTEXTUALIZADOS
ANÁLISIS FUNCIONES MATEMÁTICAS BACHILLERATO
INTEGRALES Y DERIVADAS, PROBLEMAS CONTEXTUALIZADOS:
PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- LA DERIVADA ES VARIACIÓN Y LA INTEGRAL ES SU OPERACIÓN INVERSA
- CÁLCULO DE INTEGRALES PARA MATEMÁTICAS DE BACHILLERATO
- OBTENCIÓN MEDIANTE INTEGRALES DE LOS CONCEPTOS DE FÍSICA ENERGÍA POTENCIAL GRAVITATORIA Y ELECTROSTÁTICA, POTENCIAL GRAVITATORIO Y ELECTROSTÁTICO. CAMPOS CONSERVATIVOS
ESTE MATERIAL SIGUE LA DINÁMICA QUE SE REFLEJA EN LA PROGRAMACIÓN PARA ESTE CURSO DE MATEMÁTICAS II DE 2º DE BACHILLERATO CIENCIAS SOCIALES: MATEMÁTICAS II APLICADAS A LAS CIENCIAS SOCIALES PARA 2º DE BACHILLERATO. DESARROLLO DE LA ASIGNATURA Y DE MATEMÁTICAS II DE 2º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA: DESARROLLO DE LA ASIGNATURA
EJERCICIOM2BECCSS3508: PAU EBAU CANARIAS 2020
Una empresa que ofrece servicios en internet tiene, en el día de más actividad del, año una demanda de datos que viene dada por la función:
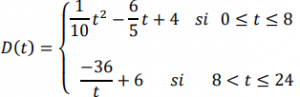
donde t es la hora del día (de 0 a 24) y 𝐷(𝑡) es la demanda de datos a esa hora expresada en cientos de Gigabits por segundo.
a) Representa gráficamente la función. ¿Hubo una demanda continua de datos a lo largo del día? En caso negativo, ¿a qué hora hubo un salto instantáneo de la demanda y cuál fue la magnitud del salto?
b) Calcula los valores de las demandas mínima y máxima absolutas y cuando se alcanzaron.
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE PROBABILIDAD Y ANÁLISIS DE FUNCIONES, PARA MATEMÁTICAS DE 2º DE BACHILLERATO CIENCIAS SOCIALES. PRUEBA 2 DEL 2º TRIMESTRE. CURSO 2025-26
EJERCICIO M1BE2205:
Se estima que en Pandora la población de sopladerus, como consecuencia de la actuación de los terrestres, varía según la expresión -40/(t+2)2 que nos indica la variación de la población en función del tiempo en miles de especímenes por mes, siendo el origen de tiempos el momento en que se consolidó la colonia de terrestres.
a.- ¿La población aumenta a lo largo del tiempo o disminuye?.
b.- Obtener la expresión de la función que determina la población de sopladerus, en función de los meses transcurridos, si se sabe que cuando se consolidó la colonia existían 30000 especímenes.
c.- Indicar a la vista de lo obtenido si la especie objeto de estudio se extinguirá en algún momento, o por el contrario se estabilizará.
d.- En caso de que se estabilice indicar el número de especímenes en el que la población, con este modelo se estabilizará.
e.- En caso de que se extinga la especie intentar una aproximación al momento en que se produce, estimándolo con una diferencia máxima permitida de 3 meses.
f.- Hallar la población total de sopladerus en los 5 primeros meses.
EJERCICIO M2BE2206:
En un plato Petri, se está probando una nueva gelatina de cultivo para un tipo especial de bacilococo. Se estima, aunque pendiente de comprobación que el número de las bacterias (en miles) sigue el modelo exponencial-logístico, en función del tiempo en horas, descrito por b(t)=6·et/(50+et).
a.- Hallar el número de bacterias que había al inicio del experimento.
b.- Hallar el número de bacterias que a la larga se alcanza cuando se consiga la estabilización de la población en el cultivo.
c.- Hallar el número total de bacterias existentes entre los tiempos t=0 y t=5, es decir la población total en ese intervalo de tiempo.
ACLARACIONES PARA ESTE APARTADO:
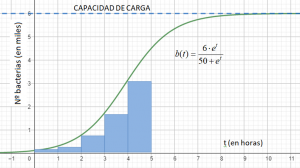
La integral nos calcula áreas encerradas como la que se muestra, haciendo un barrido en el intervalo considerado, en nuestro caso de cero a cinco horas, contando todas las bacterias que existen o existieron en ese intervalo de tiempo.
Por ello, esta respuesta coincide con la integral definida entre 0 y 5 de la función b(t):
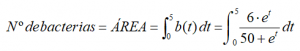
Comprobar que «más o menos» coincide con la suma de las áreas de los rectángulos azules dibujados (a falta de los trozos que faltan). La integral es más exacta que nosotros, que hemos elegido rectángulos de base igual a 1 hora, ya que la integral definida es como si hiciera rectángulos de base infinitesimal (de base dt), esto es, de base infinitamente pequeñas, con lo que no deja ningún huequito sin contar. La integral suma todos esos rectángulos desde el límite inferior al límite superior.
De hecho, en su origen, por eso de que la integral es una suma, el símbolo para la integral definida era el del sumatorio «Σ», que con el tiempo se ha ido modificando al actual «∫», que no deja de ser una «S».
CON RESPECTO A LA REPRESENTACIÓN QUE SE MUESTRA:
Corresponde a un modelo de crecimiento esperado y habitual en bacterias y poblaciones específicas (modelo logístico), mientras se cumplan una serie de condiciones. Notar como tiene una zona de crecimiento importante y termina estabilizándose.
EJERCICIO M2BE2072:
La finca de la familia Sarandonga está delimitada por la función f(x)=x3+x2-2x y el eje OX, o el eje X, o el eje de abscisas, o como tú quieras designarlo. La finca está dividida en dos partes, ya que el río Arzúa, que pasa exactamente por el eje Y, hace una división natural de la misma. La parte izquierda del río la va a heredar Alberto y la parte derecha JL, dos hermanos de distinto padre y madre que no se llevan muy bien que digamos. Haz un esbozo de la finca. ¿Qué porcentaje de la finca heredó cada uno de los hermanos?
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/JtbE5rsDeS4
ESTE EJERCICIO FORMA PARTE DE UN EXAMEN DE MATEMÁTICAS DE 2º DE BACHILLERATO QUE INCLUYE TODOS LOS CONTENIDOS. PARA SU CONSULTA SI SE DESEA: https://achimagec.com/examen-matematicas-2o-bachillerato-ciencias/
EJERCICIO M2BE2192:
La finca Los Naranjos, está delimitada por las funciones f(x) = x3 – 6x2 + 9x y g(x) = 4x. Los Naranjos tiene dos regiones, la región 1 (a la izquierda) y la región 2 (a la derecha). La región 1 es urbanizable, con un valor de 8000 euros el metro cuadrado, y la región 2 es rústica, por lo tanto, el valor del metro cuadrado es mucho menor, exactamente 187.5 euros el metro cuadrado. Si las regiones se venden independientemente, ¿Qué región aconsejarías que se comprara? ¿Por qué? Dibuja la finca Los Naranjos.
IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DEL EJERCICIO: PRUEBA DE EXAMEN DE MATEMÁTICAS II, 2º DE BACHILLERATO. ANÁLISIS, ÁLGEBRA DE MATRICES, GEOMETRÍA Y PROBABILIDAD
EJERCICIO M2BE2278:
Un agricultor llamado OMAR, se compró un terreno rústico en Santa Brígida. El terreno, está limitado por las funciones:
f(x) = x2 – 4x + 4 y g(x) = – x2 + 4
Suponemos que el gráfico está en metros.
a.- Realiza un gráfico del terreno que adquirió Omar.
b.- Calcula el precio del terreno, si cada metro cuadrado en Santa Brígida tiene un valor aproximado de 18500 euros. Alberto dice que costó menos de 48000 euros ¿está en lo cierto?.
IR A LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS II DE 2º DE BACHILLERATO. CURSO 2023-24
EJERCICIO M2BE2208:
La velocidad de cierta partícula que lleva un movimiento rectilíneo horizontal, en función del tiempo responde a la ecuación v(t) = 15/(t+1) (m/s).
El sistema de referencia se ha elegido de forma que en el origen de los tiempos la posición x es de -3 m. Se pide:
a.- ¿Se trata de un movimiento uniformemente acelerado, es decir, con aceleración constante?
b.- ¿Es un movimiento acelerado propiamente dicho o por el contrario es retardado?
c.- Obtener la ecuación del movimiento (ecuación de la posición en función del tiempo).
d.- Indicar el instante de tiempo en el que la partícula pasa por el origen del sistema de referencia.
e.- La aceleración en el instante de tiempo t=4 segundos.
IR A LA RESOLUCIÓN PASO A PASO DEL EJERCICIO, DONDE SE UTILIZA ESTE MOVIMIENTO VARIADO COMO CONTEXTUALIZACIÓN DEL USO DE INTEGRALES Y DERIVADAS: ANÁLISIS EN PROFUNDIDAD DE UN MOVIMIENTO VARIADO COMO APLICACIÓN DE LAS DERIVADAS E INTEGRALES EN FÍSICA. PROBLEMAS CONTEXTUALIZADOS.
EJERCICIO M2BE2991:
La rentabilidad (en %) de un fondo de inversión inmobiliario se obtiene mediante la función:

donde 𝑡 es el tiempo (en años) que el dinero permanece invertido en el fondo.
a) ¿Es continua la función de rentabilidad? Justifica la respuesta. (0,75 puntos)
b) ¿Cuándo crece y cuando decrece esta función? Justifica la respuesta (0.75 puntos)
c) ¿Para qué valor de t se alcanza la rentabilidad máxima? ¿Cuánto vale dicha rentabilidad? Representa gráficamente la función.
IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE MATEMÁTICAS II, DE 2º BACHILLERATO: ANÁLISIS, ÁLGEBRA Y GEOMETRÍA ESPACIAL. CURSO 2024-25
EJERCICIO M2CS2984:
Una empresa fabrica, entre otros, un tipo de artículo que vende a 520 € la unidad. Los costes de producción que tiene la empresa en la fabricación de dicho artículo vienen dados por la fórmula C(x) = x2 + 20x + 40000 , en donde x representa las unidades producidas.
a) Expresar, en función de las unidades de fabricación, el beneficio que obtiene la empresa con dicho artículo. Representar gráficamente dicho beneficio.
b) ¿Cuántas unidades de dicho artículo se deben producir para que el beneficio sea máximo?
IR AL ARTÍCULO CON LA SOLUCIÓN DE ESTE EJERCICIO: EXAMEN RESUELTO DE MATEMÁTICAS II PARA CIENCIAS SOCIALES: PROBABILIDAD, ESTADÍSTICA, INTERVALOS DE CONFIANZA Y FUNCIONES
EJERCICIO M2BE2215, DE CONTEXTUALIZACIÓN DE DERIVADAS E INTEGRALES A TRAVÉS DEL MOVIMIENTO ARMÓNICO SIMPLE:
El sonido es un movimiento ondulatorio que necesita un medio material para propagarse; de hecho, no se propaga en el vacío. El motivo de lo anterior es que cuando el sonido se genera en la fuente (las cuerdas vocales por ejemplo) las partículas del medio vibran en la misma dirección que la de propagación del sonido en un movimiento de vaivén que se transmite de una partícula a la siguiente, hasta que al final llega al receptor (el oído por ejemplo) que capta la vibración. Este movimiento de vaivén, de cada una de las partículas alcanzadas por la onda se describe mediante el Movimiento Armónico Simple (M.A.S.).
Notar como cada partícula alcanzada por la perturbación generada vibra como si de un péndulo se tratase, alcanzando dos posiciones extremas en torno a la posición de equilibrio.
Un determinado sonido se propaga en una dirección horizontal, de tal manera que las partículas del medio vibran horizontalmente en torno a su posición de equilibrio con una velocidad de vibración descrita por la ecuación v(t)= 0,003·π·cos (πt) [m/s].
a.- Para una determinada partícula alcanzada por la perturbación anterior, tomando el origen de tiempos (t=0) cuando la partícula se encuentra en su posición de equilibrio (x=0). Hallar la ecuación del movimiento x(t).
b.- Sabiendo que se denomina amplitud a la máxima deformación que presenta la partícula que vibra, hallar la amplitud del movimiento de la partícula que lleva este M.A.S.
c.- Hallar la expresión de la aceleración en función del tiempo.
d.- Expresar la aceleración en función del tiempo a(t) en función de la posición x(t).
e.- A la vista de las expresiones cinemáticas x(t), v(t) y a(t), indicar para cada una de ellas dónde se anulan y dónde alcanzan su valor máximo e indicarlo.
EJEMPLO DE USO DE LAS SUCESIVAS DERIVADAS EN EL MOVIMIENTO ARMÓNICO SIMPLE:
CUANDO TOMAMOS LA ECUACIÓN DEL MOVIMIENTO ARMÓNICO SIMPLE Y LA DERIVAMOS PODREMOS OBTENER LA EXPRESIÓN DE LA VELOCIDAD Y DE LA ACELERACIÓN DEL MOVIMIENTO ARMÓNICO SIMPLE. OBTENDREMOS POR LO TANTO LAS ECUACIONES CINEMÁTICAS DEL M.A.S.:
EJERCICIOM2BECS2949:
A principios de 2024, tras más de dos años y medio después de la erupción del volcán Tajogaite, se han comenzado a sembrar las primeras fincas de plátanos sobre las coladas de dicho volcán. Una de las fincas replantadas sobre la colada tiene una superficie, en hectáreas, limitada por las funciones f(x) = (x-2)2 y g(x) = – x + 4
a) Representa la superficie de la finca.
b) Calcula el área.
c) Si la finca produce anualmente 45000 kg de plátanos por hectárea y la Unión Europea aporta una ayuda de 0,33 euros por kilo producido ¿Cuál sería el importe a recibir cada año en ayudas de la UE sabiendo que aproximadamente el 1,5% de la producción se desecha antes de recibir las ayudas?.
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMENES RESUELTOS DE PROBABILIDAD, ESTADÍSTICA Y ANÁLISIS DE FUNCIONES, PARA MATEMÁTICAS II APLICADAS A LAS CIENCIAS SOCIALES DE 2º DE BACHILLERATO. SEGUNDO TRIMESTRE 2024-25
EJERCICIO M2CCSSBE3074:
La función G(x) da la ganancia anual (en cientos de miles de euros) obtenida por una empresa de telefonía móvil en función del tiempo x (en años) transcurrido desde su creación:

a) ¿A cuánto asciende la ganancia transcurridos dos años y medio? ¿Y transcurridos cuatro años?
b) Estudiar los intervalos de crecimiento y decrecimiento de dichas ganancias. Justificar la respuesta.
c) ¿Qué sucede a medida que transcurre el tiempo? Razonar la respuesta.
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN RESUELTO MATEMÁTICAS II CCSS. 2º DE BACHILLERATO. TERCER TRIMESTRE PRUEBA 1 DEL CURSO 2024-25.
EJERCICIO M2BE3227 (PAU 2025 Convocatoria Extraordinaria-Julio Canarias):
El modelo logístico es un modelo matemático utilizado para describir la evolución de una población a lo largo del tiempo, cuando los recursos son limitados. Es uno de los modelos matemáticos más comunes en biología y describe cómo la población se estabiliza cuando alcanza la capacidad de carga del entorno, esto es, el tamaño máximo que puede alcanzar una población antes de que los recursos se vuelvan insuficientes, lo que genera competencia y, en muchos casos, una desaceleración de la tasa de crecimiento o una crisis en la población.
Un ejemplo de modelo logístico lo encontramos en las colonias de hormigas, que están compuestas por una red de túneles, entradas, cámaras de cría y áreas de almacenamiento, donde las hormigas establecen su hábitat.
Un grupo de investigadores ha estudiado el momento en el que unas hormigas forman una nueva colonia y ha modelizado el número de hormigas (H(t)) después de t meses con la función:
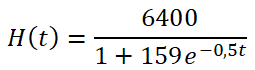
a) ¿Cuántas hormigas formaron la nueva colonia inicialmente?
b) ¿Cuál es la tasa media de crecimiento el primer año? ¿Y el segundo año? Interpretar el resultado.
PARA ESTE APARTADO PUEDE INTERESAR LA CONSULTA DEL SIGUIENTE ARTÍCULO: EJERCICIO M2BE3227 DE ANÁLISIS DE FUNCIONES CONTEXTUALIZADO, PARA MATEMÁTICAS DE BACHILLERATO. PAU CANARIAS JULIO 2025
c) Un observador afirma que el modelo siempre es creciente y entiende que la población de hormigas crece sin control. Justificar matemáticamente si esta afirmación es o no correcta.
d) ¿En qué momento la colonia de hormigas alcanzará la mitad de su capacidad de carga?
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO P.A.U. CANARIAS JULIO 2025 MATEMÁTICAS II. CONVOCATORIA EXTRAORDINARIA
EJERCICIO M2BE3220 (PAU 2025 Convocatoria Ordinaria-Junio Canarias):
En un hospital de las Islas Canarias, un equipo de investigación está analizando cómo se metaboliza en sangre un nuevo medicamento llamado Metabolix, utilizado para tratar infecciones bacterianas. La concentración residual del fármaco en el plasma sanguíneo, denotada como f(x) (medida en miligramos por litro, mg/L), depende del tiempo transcurrido x (en horas) desde su administración. El estudio indica que el medicamento sigue dos fases diferenciadas:
- Fase de absorción: En las primeras dos horas, el fármaco se distribuye por el organismo.
- Fase de eliminación: A partir de la segunda hora, el fármaco empieza a eliminarse.
Este comportamiento se modeliza mediante la siguiente función matemática:
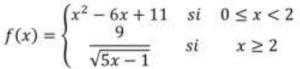
El equipo de investigación necesita aclarar algunas dudas del modelo matemático:
a) Confirmar si este modelo es realmente continuo. Justifica tu respuesta.
b) La concentración residual varía con el tiempo, comprobar que la velocidad de crecimiento instantánea de la concentración residual a las 3 horas de administrar Metabolix es mayor que -0.5 (mg/L)/h.
c) ¿Es cierto que la concentración residual del fármaco en la sangre siempre va disminuyendo con respecto al tiempo transcurrido? Averiguar en qué instante la concentración residual es máxima у calcular el valor de dicha concentración.
d) Pasado un largo periodo de tiempo, ¿cuál será la concentración residual de este medicamento?
IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE ANÁLISIS DE FUNCIONES CONTEXTUALIZADO: EJERCICIO M2BE3220 RESUELTO, CONTEXTUALIZADO DE ANÁLISIS. PAU CANARIAS JUNIO 2025
EJERCICIO M2BE3332:
La profesora Bárbara tiene un jardín en su casa. El jardín está delimitado por las funciones f(x) = x2 – 2x + 1 y g(x) = – x2 + 4x + 1. Suponiendo que el gráfico está en metros.
a) Realiza el boceto del jardín de la casa de Bárbara.
b) Bárbara va a plantar calabazas en el jardín para regalárselas a sus estimados alumnos, gastando en cada metro cuadrado de jardín 35 euros en semillas. Si va a plantar todo el jardín de calabazas, ¿Cuánto va a gastar Bárbara en la plantación?
IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE MATEMÁTICAS II, 2º BACHILLERATO. ANÁLISIS DE FUNCIONES. PRUEBA 1 DEL PRIMER TRIMESTRE DEL CURSO 25-26
EJERCICIO M2BE2442:
Hallar la función polinómica 𝑓(𝑥) que verifica que tiene un punto mínimo en 𝑀(2,-10) y su segunda derivada es: f’’(x) = x + 4 . Dar la expresión de 𝑓(𝑥).
IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTA INTEGRAL: EXAMEN RESUELTO BLOQUE ANÁLISIS FUNCIONES. MATEMÁTICAS II DE 2º BACHILLERATO. PRUEBA 3 DEL PRIMER TRIMESTRE 2025-26.
