EXAMEN RESUELTO PAU 2025
MATEMÁTICAS II JULIO EXTRAORDINARIA
EXAMEN RESUELTO P.A.U. CANARIAS JULIO 2025. CONVOCATORIA EXTRAORDINARIA:


INTERESA LA CONSULTA DEL SIGUIENTE CONTENIDO RELACIONADO: EXAMEN RESUELTO P.A.U. CANARIAS JUNIO 2025 MATEMÁTICAS II. CONVOCATORIA ORDINARIA
PARA LA PREPARACIÓN DE LA PRUEBA O UNA SIMILAR CONVIENE LA CONSULTA DE LOS SIGUIENTES MATERIALES DE ESTE PROYECTO DE MEJORA DEL APRENDIZAJE EN CIENCIAS:
-
- FUNCIONES: ANÁLISIS PARA 1º BACHILLERATO
- TABLA DE DERIVADAS
- APLICACIONES DE LA DERIVADA. OPTIMIZACIÓN Y CÁLCULO DE PARÁMETROS.
- GEOMETRÍA ESPACIAL PARA BACHILLERATO
- EJERCICIOS DE CÁLCULO DE PROBABILIDADES PARA MATEMÁTICAS DE 2º BAC
- MATRICES Y DETERMINANTES PARA BACHILLERATO.
- EXÁMENES RESUELTOS PASO A PASO DE MATEMÁTICAS 2º BACHILLERATO
SIGUE EL ESQUEMA PLANTEADO PARA EL SEGUIMIENTO DE LA ASIGNATURA DE MATEMÁTICAS II DE 2º DE BACHILLERATO: MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
LOS ENUNCIADOS DE LA PRUEBA PAU JULIO 2025 EXTRAORDINARIA, PÁGINA 1:
LOS ENUNCIADOS DE LA PRUEBA PAU JULIO 2025 EXTRAORDINARIA, PÁGINA 2:
LOS EJERCICIOS Y SU RESOLUCIÓN PASO A PASO:
EJERCICIO M2BE3227:
El modelo logístico es un modelo matemático utilizado para describir la evolución de una población a lo largo del tiempo, cuando los recursos son limitados. Es uno de los modelos matemáticos más comunes en biología y describe cómo la población se estabiliza cuando alcanza la capacidad de carga del entorno, esto es, el tamaño máximo que puede alcanzar una población antes de que los recursos se vuelvan insuficientes, lo que genera competencia y, en muchos casos, una desaceleración de la tasa de crecimiento o una crisis en la población.
Un ejemplo de modelo logístico lo encontramos en las colonias de hormigas, que están compuestas por una red de túneles, entradas, cámaras de cría y áreas de almacenamiento, donde las hormigas establecen su hábitat.
Un grupo de investigadores ha estudiado el momento en el que unas hormigas forman una nueva colonia y ha modelizado el número de hormigas (H(t)) después de t meses con la función:
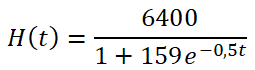
a) ¿Cuántas hormigas formaron la nueva colonia inicialmente?
b) ¿Cuál es la tasa media de crecimiento el primer año? ¿Y el segundo año? Interpretar el resultado.
PARA ESTE APARTADO PUEDE INTERESAR LA CONSULTA DEL SIGUIENTE ARTÍCULO: TASA DE VARIACIÓN MEDIA, INSTANTÁNEA, DERIVADA: DEFINICIÓN. EJERCICIOS RESUELTOS
c) Un observador afirma que el modelo siempre es creciente y entiende que la población de hormigas crece sin control. Justificar matemáticamente si esta afirmación es o no correcta.
d) ¿En qué momento la colonia de hormigas alcanzará la mitad de su capacidad de carga?
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO M2BE3227 DE ANÁLISIS DE FUNCIONES CONTEXTUALIZADO, PARA MATEMÁTICAS DE BACHILLERATO. PAU CANARIAS JULIO 2025
EJERCICIO M2BE3228:
En la fabricación de piensos para peces en granjas acuícolas, es necesario equilibrar la cantidad de proteína, grasa y carbohidratos. Una empresa dedicada a los piensos para peces utiliza tres tipos principales de materias primas, las cuales proporcionan diferentes cantidades de proteína, grasa y carbohidratos. Las materias primas son: subproductos vegetales que contienen un 20% de proteína, un 10% de grasa y un 10% de carbohidratos; harinas que aportan un 40% de proteínas, un 20% de grasa y un 30% de carbohidratos; y subproductos cárnicos que aportan un 60%, 10% y 30% respectivamente.
Esta empresa productora está preparando 1000 kg de pienso que han de contener un 36% de proteína, un 12% de grasa y un 20% de carbohidratos. ¿Qué cantidad de cada materia prima se ha de utilizar para obtener el pienso con las características indicadas?
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE3228 DE SISTEMA DE ECUACIONES POR EL MÉTODO DE CRAMER. PAU CANARIAS JULIO 2025
EJERCICIO M2BE3229:
Resolver el siguiente sistema de ecuaciones matriciales:
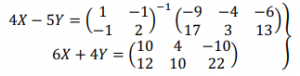
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE3229 DE SISTEMA DE ECUACIONES MATRICIALES. PAU CANARIAS JULIO 2025
EJERCICIO M2BE3230:
En el espacio tridimensional, se considera la recta y plano siguientes:
![]()
a) Comprobar que el plano 𝜋 y la recta r se cortan. Dar la ecuación de la recta 𝑠, contenida en el plano 𝜋, que corta perpendicularmente a 𝑟.
b) Hallar el ángulo que forman la recta 𝑟 y el plano 𝜋.
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO M2BE3230, RESUELTO DE GEOMETRÍA ESPACIAL PARA BACHILLERATO. POSICIONES RELATIVAS RECTA Y PLANO. PAU CANARIAS JULIO 2025
EJERCICIO M2BE3231:
En el espacio tridimensional, se tienen las siguientes rectas:
![]()
a) Comprobar que r y s son coplanarias.
POSICIONES RELATIVAS DE DOS RECTAS EN EL ESPACIO, PARA MATEMÁTICAS II DE 2º BACHILLERATO
b) Hallar la ecuación del plano que las contiene.
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO M2BE3231, RESUELTO DE GEOMETRÍA ESPACIAL PARA BACHILLERATO. RECTA Y PLANO. PAU CANARIAS JULIO 2025
EJERCICIO M2BE3232:
Se está desarrollando una prueba para detectar una enfermedad rara que afecta al 1% de la población adulta. Se sabe que, la sensibilidad de la prueba (dar positivo cuando la persona está enferma) es del 95%, y la especificidad de la prueba (dar negativo cuando la persona está sana) es del 98%. Se selecciona al azar un individuo de la población:
a) Si se somete a la prueba de diagnóstico, calcular la probabilidad de que esté realmente enfermo cuando la prueba da positivo.
b) Si una población de 35000 individuos se somete a la prueba, ¿podríamos afirmar que se espera que habrá más de 50 personas que estarán enfermas, aún cuando han obtenido un resultado negativo en el test?
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE3232, DE PROBABILIDAD DIAGRAMA EN ÁRBOL. PAU CANARIAS JULIO 2025
EJERCICIO M2BE3233:
El Instituto Canario de Estadística (ISTAC) se ha encargado de realizar un estudio multidisciplinar para optimizar la planificación de plazas en residencias universitarias de estudiantes de nuevo ingreso en las dos universidades públicas canarias (ULL y ULPGC).
Para ello, se ha llevado a cabo una encuesta a 1800 estudiantes de nuevo ingreso que provienen de islas no capitalinas, de los que el 27% de estos estudiantes solicitan plaza en una residencia universitaria.
a) Comprobar si hay más de un 90% de posibilidades de recibir entre 460 y 510 solicitudes de plaza en una residencia de estudiantes de nuevo ingreso que provienen de islas diferentes a Tenerife y Gran Canaria.
b) A partir de 525 solicitudes de alojamiento de estos estudiantes, las universidades deberían acometer la construcción de nuevas residencias universitarias. ¿Qué probabilidad hay de que deban adoptar esta medida?
IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE3233 DE PROBABILIDAD. APROXIMACIÓN DE LA BINOMIAL A LA NORMAL. PAU CANARIAS JUNIO 2025
